建筑制图-回转体的正等测图技巧

画回转体的轴测投影，应首先掌握圆的正等测投影，特别是要掌握与坐标面平行或重合的圆的正等测投影的画法。

1.圆柱的正等测图

例5-9　作如图5-27所示圆柱体的正等轴测图。

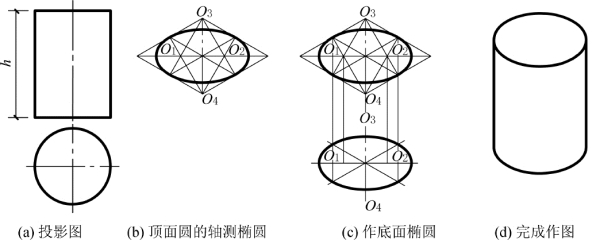
图5-27　例5-9图

分析　用四心法作顶面和底面的椭圆，然后作两椭圆的公切线，即为柱面轴测投影的外形轮廓线。注意，该外形轮廓线不同于圆柱正面投影中外形轮廓线的轴测图。

作图　（1）用四心法作顶面圆的轴测椭圆，如图5-27（b）所示。

（2）将顶面椭圆中心及四个圆心向下平移（移心法）柱高h，以此作底面椭圆，如图5-27（c）所示。

（3）作两椭圆的公切线。

（4）擦去多余线及不可见曲线，完成作图，如图5-27（d）所示。

从图5-27（c）可知，圆柱底面后半部分不可见，故不必画出。由于上、下两椭圆完全相等，且对应点之间的距离均为圆柱高度h，所以只要完整地画出顶面椭圆，则底面椭圆的三段圆弧的圆心以及两圆弧相连处的切点，沿Z1轴方向向下量取高度h即可找出。这种方法称为移心法，可简化作图过程。

轴线垂直于V面、W面的正圆柱的轴测图画法与垂直于H面的相同，只是椭圆长轴方向随圆柱的轴线方向而异，即圆柱顶面、底面椭圆的长轴方向与该圆柱的轴线垂直，如图5-28所示。

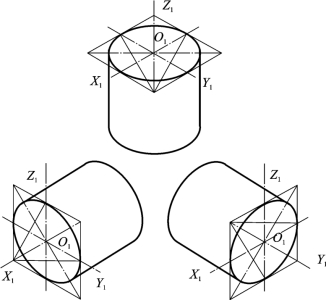
图5-28　三个方向圆柱的正等测图

2.斜截圆柱的正等测图

例5-10　作出图5-29（a）所示形体的正等测图。

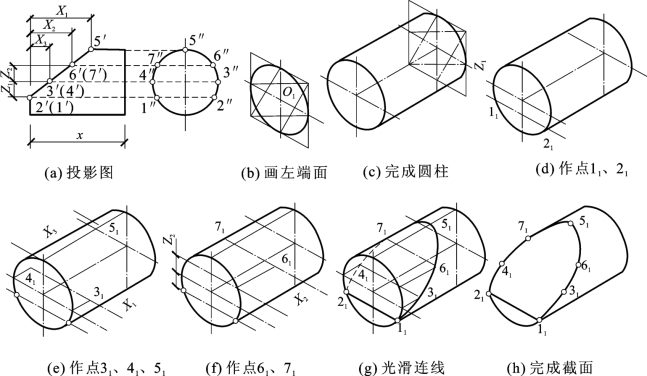
图5-29　截交线的正等测图画法

分析　由投影图可知，圆柱被一个平面截切，截切后的截交线是椭圆弧。作图时应先画出未截切之前的圆柱，再画斜截面。

作图

（1）画圆柱的左端面。选定轴测轴，画外切菱形和四心椭圆，如图5-29（b）所示。

（2）沿O1X1轴向右量取X，作右端面椭圆，作平行于O1Y1轴的直线与两椭圆相切，完成圆柱的正等测图，如图5-29（c）所示。

（3）用坐标法画出截面上—系列的点。先作最低点11和21。可在左端面上沿O1Z1轴向下量取Z1，再引线平行于O1Y1轴，交椭圆于点11、21，如图5-29（d）所示。再作最前点31、最后点41和最高点51。分别过中心线与椭圆的交点引平行于O1X1轴的圆柱素线，对应量取X1和X2，得点31、41和51，如图5-29（e）所示。在适当位置作中间点。先在投影图上选定点61、71，再沿O1Z1向上量取Z2，沿O1X1向右量取X2，可得点61和71，如图5-29（f）所示。(www.xing528.com)

（4）用直线连接点11、21，用圆滑曲线依次连接其余各点，如图5-29（g）所示。

（5）擦去作图线，即为所求，如图5-29（h）所示。

3.相交两圆柱的正等测图

例5-11　作出图5-30（a）中两相贯圆柱的正等测图。

分析　此两圆柱正交，相贯线为空间曲线，需求出若干共有点的轴测投影，以完成此空间曲线的轴测投影。

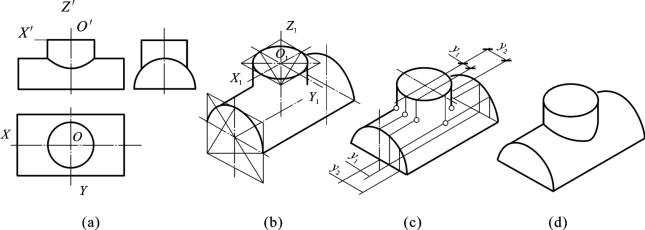
图5-30　相贯线的轴测图画法

作图

（1）引入直角坐标系，如图5-30（a）所示。

（2）画轴测轴后，作出直立圆柱和水平圆柱，如图5-30（b）所示。

（3）以平行于X1O1Z1面的平面截切两圆柱，分别获得两组截交线，该两组截交线的交点均为相贯线上的点，如图5-30（c）所示。

（4）用曲线光滑地连接各点，擦去作图线，并加深，如图5-30（d）所示。

例5-12　试画出图5-31（a）所示形体的正等测图。

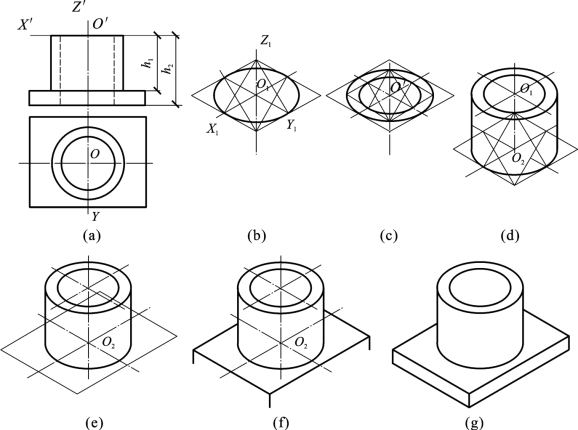
图5-31　组合体的正等测图

分析　从给出的正投影图可知，该形体是一个组合体；由方板和圆筒叠加而成，因此可按叠加法，先画圆筒，后画方板。

作图

（1）画顶面外椭圆：以O1为圆心画轴测轴，画外切菱形和四心椭圆，如图5-31（b）所示。

（2）用同样的方法画顶面内椭圆，如图5-31（c）所示。

（3）完成圆筒：沿O1Z1轴从O1点往下量取h1得到O2，以O2为原点画轴测轴。用同样的方法画出底面椭圆。作平行于O1Z1轴的直线与两椭圆相切，完成圆柱的正等测图，如图5-31（d）所示。

（4）利用圆筒底面的轴测轴，画出方板顶面，如图5-31（e）所示。

（5）用端面延伸法，将方板顶面的四角顶点沿O1Z1轴往下平移一个方板的厚度（h2-h1），如图5-31（f）所示。

（6）画出方板底面的边线，整理并加深可见轮廓线，完成整个形体的正等测图，如图5-31（g）所示。