圆柱与圆锥相交-建筑制图，示例及作图求解

例4-13　如图4-23所示，求圆柱与圆锥的相贯线。

分析　圆柱面为侧垂面，其W面投影为圆，相贯线的W面投影在此圆上。为了作出相贯线的另两面投影，选取水平面作为辅助平面。从图4-23（a）可看出，水平辅助平面P与圆柱面交于两条直素线，与圆锥面交于和圆锥底面平行的圆。直素线与圆同在平面P内，它们的交点A、B为圆柱面、圆锥面和平面P的共有点（三面共点），所以是相贯线上的点。作若干水平辅助平面，可得到一系列的共有点，连点成光滑曲线即为所求的相贯线。

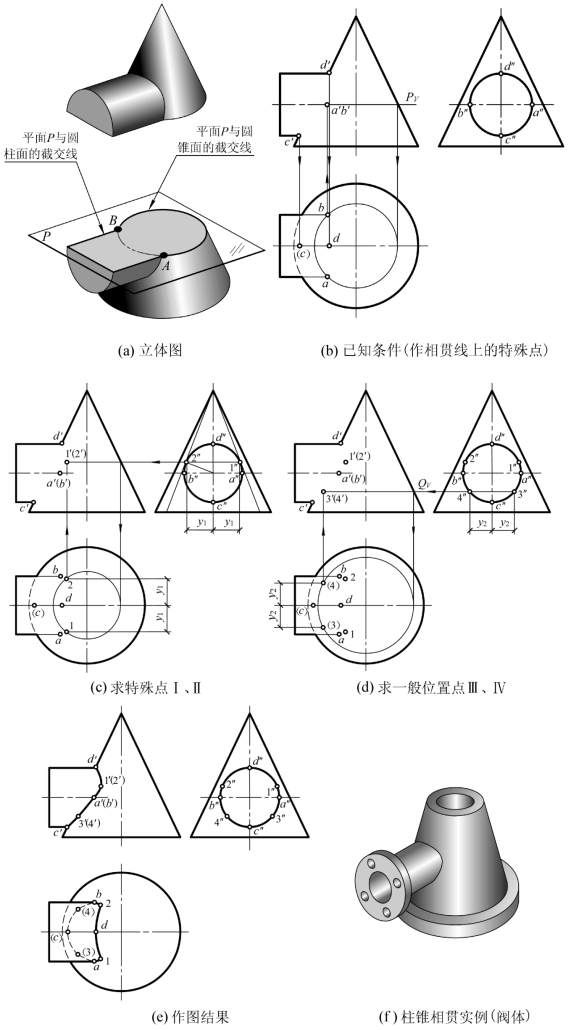
图4-23　圆锥体与圆柱体相贯线的画法(www.xing528.com)

作图　（1）求特殊点。如图4-23（b）所示，从W面投影可直接确定相贯线上的特殊点A、B、C、D的W面投影a″、b″、c″、d″。由c′、d′作投影线与圆柱面的H面投影轴线相交得c、d；过圆柱轴线作水平辅助平面P，平面P与圆柱面的交线（两条直素线）、与圆锥面的交线（水平圆）的H面投影的交点即为A、B两点的H面投影a、b，作投影线与圆柱面的V面投影轴线相交得a′、b′。

（2）求极限点。点Ⅰ、Ⅱ是相贯线上的最右极限点，这两点的三面投影可采取表面定点的方法得到，作图过程如图4-23（c）所示。

（3）求一般位置点。采用水平辅助平面Q，求得点Ⅲ、Ⅳ的三面投影，作图过程如图4-23（d）所示。

（4）用光滑的曲线连接各点的同面投影。因为该相贯体形状前后对称，所以相贯线的V面投影前后重影，将点d′、1′、a′、3′、c′光滑地连接起来，即为所求相贯线的V面投影。点a和点b是相贯线H面投影可见与不可见的分界点，因为从上往下看，只有圆柱面的上半部分与圆锥面的交线才是可见的，将点a、1、d、2、b光滑地连接成实线，将点b、（4）、（c）、（3）、a光滑地连接成虚线，即为所求相贯线的H面投影。