平面立体是由若干个平面围成的立体。常见的平面立体有棱柱、棱锥和棱台。平面立体的三面投影图就是各平面以及平面与平面相交棱线的投影,因此作平面立体的投影时,应分析围成立体的各个平面以及棱线的投影特点,并注意投影中的可见性和重影问题。
1.棱柱
棱柱是由上、下底面和若干侧面围成的基本形体(见图4-1、图4-2)。棱柱的上、下底面形状大小完全相同且相互平行;每两个侧面的交线为棱线又称为侧棱,有几个侧面就有几条侧棱线。侧棱垂直于底面的棱柱称为直棱柱,侧棱不垂直于底面的棱柱称为斜棱柱。本任务只讨论直棱柱。
图4-2(a)所示的是六棱柱,上下底面为六边形是水平面,前后2个侧面为长方形是正平面,左右4个侧面为长方形是铅垂面。将六棱柱分别向三个投影面投影,得到的三面投影图如图4-2(b)所示。

图4-1 棱柱
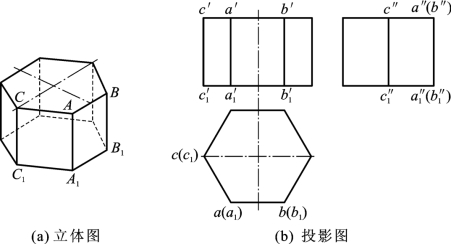
图4-2 正六棱柱的投影
分析六棱柱的三面投影图可知:水平投影面为六边形,从形体的平面投影的角度看,它可以看作上下底面的重合投影(上底面可见,下底面不可见),并反映实形,六边形的边也可以看作垂直于水平投影面的六个侧面的积聚投影。
正面投影为三个长方形,中间的长方形投影可看成前后2个平行于正投影面的侧面的重合投影(前侧面可见,后侧面不可见),并反映实形。两侧的长方形投影可看作左右侧面的投影,但均不反映实形。上下底面的积聚投影是正面投影的最上和最下的两条横线。
侧面投影为两个长方形,它是左右4个侧面的重合投影(左侧面可见,右侧面不可见),但均不反映实形。左右2个侧面投影积聚为侧面投影的左右两条边线,上下底面的积聚投影是最上和最下的两条横线。
2.棱锥(https://www.xing528.com)
由一个底面和若干个侧面围成,各个侧面的各条棱线相交于顶点的形体称为棱锥。顶点常用字母S来表示,顶点到底面的垂直距离称为棱锥的高。三棱锥底面为三角形,有3个侧面及3条棱线;四棱锥的底面为四边形,有4个侧面及4条棱线;依次类推。
图4-3(a)所示为一个三棱锥,顶点为S,三条棱线分别为SA、SB、SC。其底面△ABC是水平面,后侧面△SAC是侧垂面,左右两个侧面△SAB和△SBC是一般位置平面。将三棱锥分别向三个投影面投影,得到的三面投影图如图4-3(b)所示。

图4-3 三棱锥的投影
分析三棱锥的三面投影图可知:水平投影面由四个三角形组成,分别是三棱锥的4个面投影形成的,其中△sab是左侧面SAB的投影,△sbc是右侧面SBC的投影,△sac是后侧面SAC的投影,△abc是底面ABC的投影。三棱锥的底面是水平面,其投影△abc反映实形,其余3个侧面的水平投影均不反映实形。
正面投影由三个三角形组成,△s′a′b′是左侧面SAB的投影,△s′b′c′是右侧面SBC的投影,△s′a′c′是后侧面SAC的投影,它们均不反映实形,投影底边a′b′c′是底面ABC的积聚投影。
侧面投影是一个三角形,它是左右侧面SAB和SBC的重合投影,不反映实形,后侧面SAC的投影积聚为边线s″a″(c″),底面ABC的投影积聚为边线a″(c″)b″。
3.棱台
棱锥的顶部被平行于底面的平面截切后即形成棱台。图4-4(a)所示的为四棱台立体图,其形体特点为:两个底面为大小不同、相互平行且形状相似的多边形,各侧面均为等腰梯形。
图4-4(b)所示为四棱台的投影图,其画法思路同四棱锥。应当注意的是:画每个投影图都应先画上、下底面,然后画出各侧棱。

图4-4 四棱台的三投影图
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




