地下结构优化：二次衬砌改进

6.4.3.1　优化的目的与意义

目前对于隧道二次衬砌的设计普遍采用均一厚度，这显然没有考虑到衬砌结构的受力特点没有充分发挥材料的性能。我们的第二方面研究内容也是核心部分研究内容即是考虑二次衬砌厚度的非均一化优化设计。具体思路将衬砌结构离散化为多个单元，以结构内力和位移为约束条件，以总的衬砌混凝土用量为目标函数，通过优化算法计算出各个离散单元的衬砌厚度最优组合，然后拟合成为连续曲线，用于指导现实施工设计。

6.4.3.2　优化方法

针对目前隧道结构优化研究发展现状，本文利用遗传算法对隧道衬砌结构进行优化设计研究。新兴的遗传算法属于一种具有多点全局概率并行技术的优化方法，在优化领域具有传统优化方法无法比拟的优点，目前在各行各业得到了推广应用。

本文做了初步具体的针对实现隧道衬砌结构的遗传算法优化设计分析的探索和研究，主要做以下几方面工作：

1）在广泛阅读文献和调研的基础上，采用荷载结构法和相应荷载计算方法，选取一定的衬砌厚度，应用有限元软件ANSYS对本工程算例进行受力分析，得出一个初始解答。

2）利用ANSYS自带的优化程序，采用零阶搜索方法得出优化解。

3）根据遗传算法原理，编写结合了遗传算法与有限元计算的衬砌优化计算程序，并将该程序计算结果与利用有限元软件ANSYS中的零阶优化方法计算所得结果进行对比。

6.4.3.3　衬砌厚度的有限元初始解

1.荷载-结构法计算模型

荷载结构模型认为地层对结构的作用只是产生作用在地下建筑结构上的荷载（包括主动地层压力和被动地层抗力），衬砌在荷载的作用下产生内力和变形，与其相应的计算方法称为荷载结构法。这一方法与设计地面结构时习惯采用的方法基本一致，区别是计算衬砌内力时需考虑周围地层介质对结构变形的约束作用。

计算时先按地层分类法或由实用公式确定地层压力，保证衬砌结构能安全可靠的承受地层压力等荷载的作用下，按弹性地基上结构物的计算方法计算衬砌的内力，并进行结构截面设计。本次计算即采用以局部弹簧单元来模拟地层反力的荷载-结构模型，如图6-66所示。其中通过迭代试算可以确定受拉区，并删去相应的弹簧单元。

图6-66　基于局部地层弹簧的荷载-结构法计算模型

2.参数设置及荷载计算

本次计算共划分42个衬砌单元如图6-67所示，取初始衬砌单元厚度全部为0.50 m。

图6-67　计算模型衬砌单元划分示意图

隧道深埋断面荷载计算方法如下：

hq——荷载等效高度（m）按下式计算：

其中　S——围岩级别；

　　　ω——宽度影响系数，ω=1+i（B-1）；

　　　B——隧道宽度；

　　　i——以B=5 m的围岩垂直均布压力为准，B每增减1 m时的围岩压力增减率，当B＜5 m时，取i=0.2；B＞5 m时，取i=0.1。

围岩垂直均布压力为

式中，r为围岩容重，k N/m3。

围岩水平向压力为

(www.xing528.com)

式中，λ为围岩侧压力系数，依据规范对于Ⅴ级围岩取0.3～0.5，本次计算取0.4。

根据以上基于局部地层弹簧的荷载结构法有限元模型及前处理程序计算所得荷载结果，由ANSYS求解其初始解的受力及变形可得如图6-68—图6-71结果。

6.4.3.4　衬砌厚度的ANSYS零阶优化

1.ANSYS的零阶优化方法

零阶方法属于直接法，它是通过调整设计变量的值，采用曲线拟合的方法去逼近状态变量和目标函数，可以很有效地处理大多数的工程问题。零阶方法之所以称为零阶方法是由于它只用到因变量而不用到它的偏导数。在零阶方法中有两个重要的概念：目标函数和状态变量的逼近方法，由约束的优化问题转换为非约束的优化问题。

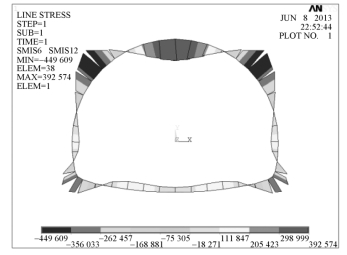
图6-68　隧道断面初步计算结果弯矩图

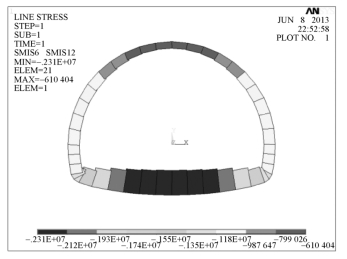
图6-69　隧道断面初步计算结果轴力图

图6-70　隧道断面初步计算结果剪力图

图6-71　隧道断面初步计算结果变形图

由于基于ANSYS的零阶优化方法在前述章节中已具体介绍，本例着重介绍衬砌厚度优化的GAFEM方法，因此本例中对于零阶优化方法仅做简单的介绍。

2.ANSYS零阶优化结果

基于ANSYS的零阶优化计算，50次迭代最优解Vtot=12.893 m3，相比于初始解14.407 9 m3，可见优化后可在一定程度上，减少了混凝土的用量，虽然各单元厚度为离散数据，在实际工程中较难以实现，但其对工程仍有实际的指导意义，如拱顶处，角部衬砌厚度可适当增厚，其余部分衬砌厚度可相应减小，以此适应衬砌的实际受力状态。

6.4.3.5　衬砌厚度的GAFEM优化

1.GAFEM优化方法概述

本工程中，由于需要在衬砌环向取得多个离散单元的厚度，因此本项内容中会出现较多的设计变量，例如我们初步计算模型划分的单元数量达到42个，考虑到对称性，设计变量也达到了21个，因此ANSYS的零阶优化方法并不能很有效的进行最优解搜索；而智能算法适用于高维最优化问题，为此需要自行设计基于荷载结构法的有限元程序，并使其实现与智能算法到的对接。本次研究即编写了基于遗传算法的有限元优化程序GAFEM来实现上述目标。

2.GAFEM优化方法流程

在GAFEM算法中，利用荷载结构法进行结构的有限元计算，而在每一次结构计算后的参数调整及优化过程中采用遗传算法，并编制荷载计算与遗传优化的对接程序来实现优化的需要。

3.GAFEM优化结果

取算法参数为：种群个体50；进化代数200；交叉概率0.8；变异概率0.15。优化结果如图6-72和图6-73所示。

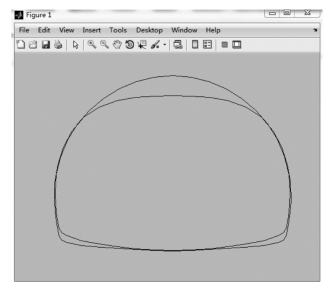
图6-72　衬砌优化后断面变形图

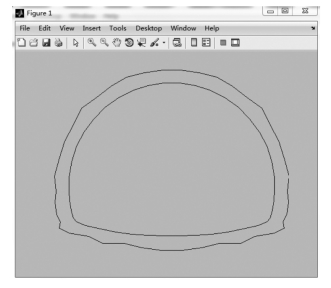
图6-73　优化后衬砌厚度分布图

由优化结果可知，最优解对应衬砌混凝土总体积为9.952 7 m3，对应于初始解对应衬砌混凝土总体积为14.407 9 m3，以及ANSYS零阶优化的最优解12.893 m3，可以发现优化结果不仅比初始解小许多，优化后体积仅为优化前的68.8%，也比ANSYS零阶优化解节约了大量混凝土体积，说明GAFEM在衬砌优化计算中是一个优秀的工具。

由以上计算结果可知，优化后衬砌厚度在隧道拱顶、仰拱中央及衔接处需取得较大值，符合隧道受力规律。而本文所拟合出的曲线还不够光滑，尚需进一步细分单元和细化计算模型来得到更进一步的结果依次来指导施工实践。