在6.2.3节中已经实现了本工程问题在ANSYS软件中的优化。鉴于数值计算软件MATLAB在优化计算方面的强大功能,本节尝试将MATLAB和ANSYS联合起来进行偏压连拱隧道衬砌结构的优化。
6.2.4.1 工程问题数学模型抽象化
MATLAB是一个数学软件,其强大的优化功能只能在已有明确的数学模型的基础上实现。而本问题是一个实际的工程问题,因而首先需要将其抽象为一个数学模型。
由于本模型采用地层——结构法计算,并且进行的是岩土体的弹塑性分析,因而是一个高度的非线性问题。从数学上来讲,其非线性主要表现在约束条件的高度非线性,即状态变量是设计变量的非线性函数,而这种非线性关系是无法给出显式表达式的。
利用有限元软件ANSYS进行数值计算,由优化工具箱的随机法(Random Designs)使设计变量在限制范围内随机变化20次,研究整个设计空间,并得到20组各状态变量和设计变量的对应数据。利用MATLAB内置拟合函数将各状态变量拟合为设计变量的3次齐次多项式,该多项式的项数表达式如下:
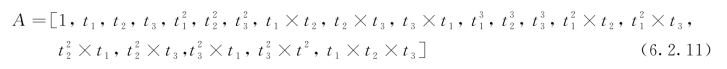
这样,该工程问题最终转化为的数学模型为:
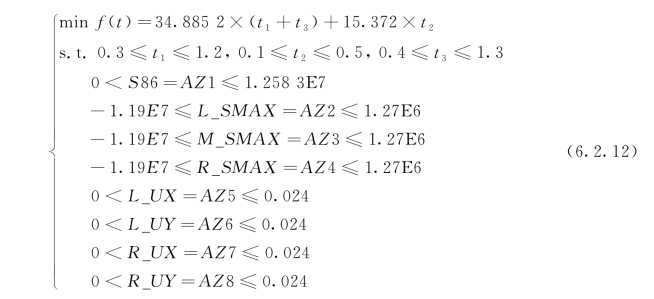
式中 f(t)——目标函数,单位米延长的衬砌总体积;
S 86——中隔墙最大MISES等效应力;
L_SMAX——隧道左洞衬砌最大应力;
M_SMAX——隧道中导洞衬砌最大应力;
R_SMAX——隧道右洞衬砌最大应力;
L_UX——隧道左洞水平收敛;
L_UY——隧道左洞竖向收敛;
R_UX——隧道右洞水平收敛;
R_UY——隧道右洞竖向收敛。
拟合得到的状态变量关于设计变量的系数矩阵见表6-12。
表6-12 由设计变量拟合状态变量的多项式系数矩阵
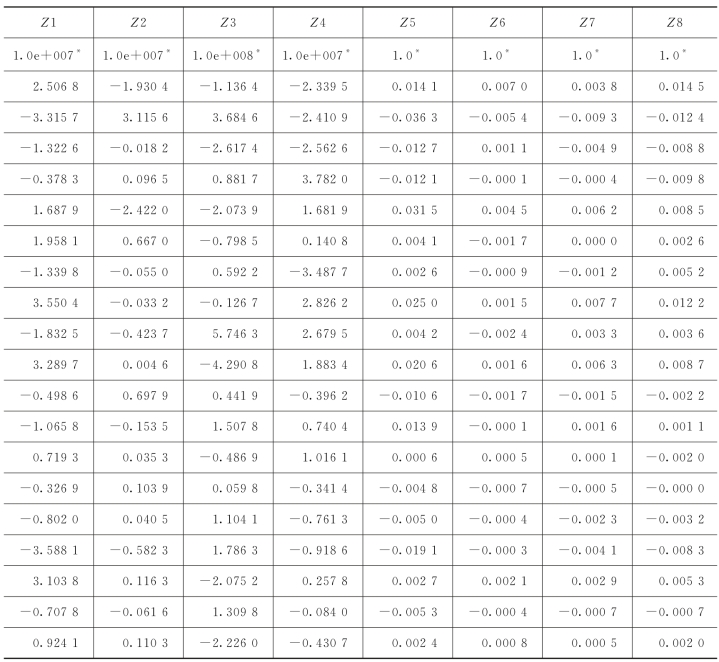
6.2.4.2 构造优化函数
本次优化计算调用MATLAB优化工具箱的有约束非线性优化函数fmincon().其表达格式为:
![]()
上式输出列表中,x为设计变量的优化值,fval为对应于设计变量的函数值,exitflag为算法终止原因输出,output是其他的相关输出选项。(https://www.xing528.com)
在输入参数列表中,fun表示优化函数;x0为设计变量初始值;A,b为满足线性关系式Ax=b的系数矩阵;Aeq和beq是满足线性等式Aeq×x=beq的系数矩阵;lb和ub是变量x的下限和上限;参数nonlcon表示满足非线性约束关系c(x)≤0和ceq(x)=0的优化情况,是本问题的主要控制指标;参数options是优化的属性设置,默认为采用大规模算法(large scale)。所谓大规模问题指的是出现在工程,化学等领域中有大量优化变量的问题。由于自变量的维数很高,这样的问题是被分解成多个低维子问题来求解的。Medium-Scale优化问题实际上是MATLAB软件包提出和大规模问题对应的一个概念,就是通常一般的优化算法,如牛顿法,最速下降法之类的处理优化变量不是很多的问题。针对本数学模型只有3个优化变量,且状态变量只是设计变量的3次表达式,选用medium scale设置。
6.2.4.3 构造非线性约束函数
对于已经抽象的数学模型而言,要调用MATLAB优化函数fmincon()的关键是构造相关非线性优化函数。在MATLAB工作空间建立如下的非线性约束函数:


6.2.4.4 构造目标函数
取连拱隧道单位米延长衬砌总体积为优化目标函数Total Volu(t),在MATLAB工作空间编写目标函数如下:


6.2.4.5 优化结果输出
在MATLAB命令窗口输入如下命令:

运行程序后输出如下:

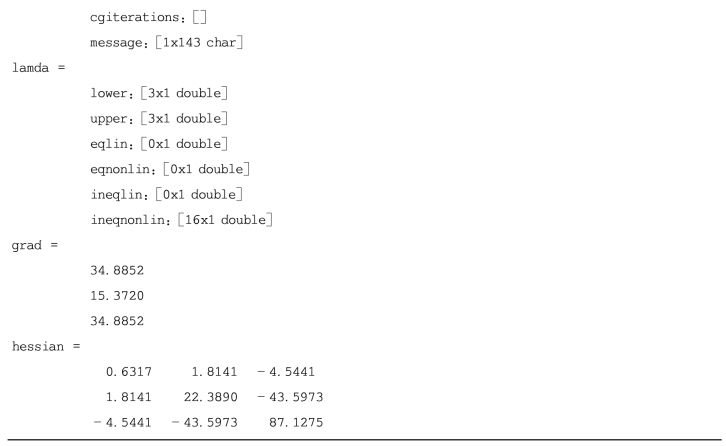
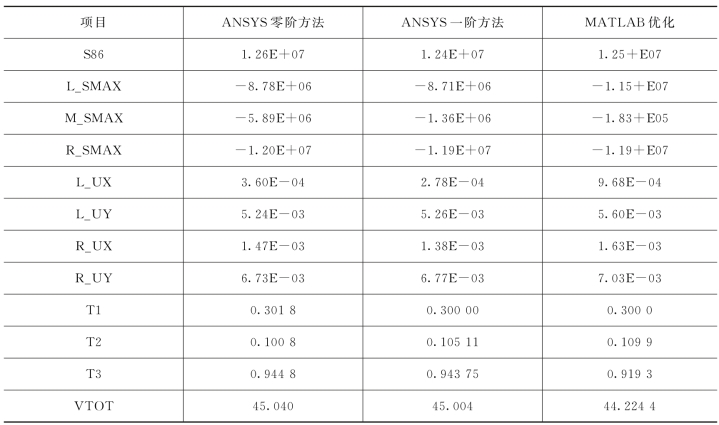
最终得到的优化结果和利用ANSYS优化的结果列于表6-13。
表6-13 利用MATLAB和ANSYS的优化结果比较
6.2.4.6 小结与思考
本节通过联合数值计算软件MATLAB和有限元计算软件ANSYS对该偏压连拱隧道衬砌结构进行优化,可以得出以下结论:
1)利用通用有限元软件ANSYS进行地下工程结构优化设计是一个可行的方法。ANSYS优化工具模块内置有零阶优化算法和一阶优化算法。零阶算法具有强大的全局寻优能力但精度较低,一阶算法计算精度较高但容易陷入局部最优解。建议在实际工程优化计算时采用零阶算法和一阶算法配合进行,可以取得较为合理的优化结果。
2)数值计算软件MATLAB具有很强的数值计算功能,其优化工具箱内置多种功能强大的优化算法。但对于实际工程问题往往难以写出约束条件的显式表达式,可以利用ANSYS先得到有限元数值计算解,然后调用MATLAB的优化函数进行优化。
3)总体上来讲,ANSYS的一阶算法精度高于零阶算法,而MATLAB的优化结果又优于ANSYS的一阶算法。如有实际 监测数据,可以考虑使用神经网络等更为高级的优化算法。
4)从优化结果来看,主洞衬砌结构的应力约束起了控制性作用。这主要是因为该连拱隧道采用的是整体式直中墙结构,衬砌在与中墙交汇处存在“尖角”,导致过大的应力集中。建议在实际工程中采用弧度更为缓和的整体式曲中墙或三层曲中墙。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




