地下结构优化：材料计算参数选取

对于地下工程的数值计算而言，材料计算参数的选取是一个常被简化处理但又十分重要的问题，因为计算参数选择的合理与否直接关系到数值计算的成败。同济大学地下建筑与工程系教授侯学渊先生就曾经说过，数值计算材料参数选取得不对，数值计算就只是“Garbage in，garbage out”，现在听来依然振聋发聩。然而，对于实际工程项目，现场地质勘察报告和岩土勘察报告给出的岩土材料的物理力学参数一般都只是一个大致的范围，而数值计算要求的材料计算参数必须是一个确定值，如何合理地解决这个矛盾呢？我们想到了以下办法。

基于普氏理论与公路隧道设计规范推荐公式在我国隧道工程界的广泛应用，可以通过该公式所得到的松动圈范围来反演数值模型中的计算参数。下面以《公路隧道设计规范》为依据，借助有限元软件ANSYS，以围岩的极限拉应变为判据给出模型材料的力学性能参数。技术路线如图6-20所示。

图6-20　技术路线

按照公路隧道设计规范

对于本节依托的双连拱隧道，单洞跨度为12 m左右，由此分别计算出Ⅳ级，Ⅴ级围岩的荷载等效高度为：

Ⅳ级围岩：h=0.45×2S-1ω=0.45×23×[1+0.1×（12-5）]=6.12 m

Ⅴ级围岩：h=0.45×2S-1ω=0.45×24×[1+0.1×（12-5）]=12.24 m

根据隧道规范，对于Ⅳ级，Ⅴ级围岩，深浅埋的分界高度为hq=2.5h，由此计算出按照隧道规范，Ⅳ级，Ⅴ级围岩深埋隧道的最小埋深分别为：15.3 m与30.6 m。实际工程中，由于地表风化层的存在以及岩体结构节理裂隙的影响，深浅埋分界标准不能完全绝对化，一般而言，覆土厚度在30～50 m为宜。

结合石吉中龙隧道实际工程，对于Ⅴ级围岩，计算选取断面为K140+200，隧道围岩为强风化变余砂岩，结构破碎，隧道埋深35 m左右；对于Ⅳ级围岩，计算选取断面为K140+235，隧道围岩为弱风化变余砂岩，结构较破碎，隧道埋深35 m左右。

由此建立起单洞隧道模型如图6-21所示：

图6-21　单洞隧道有限元数值模型

一般而言，岩石在力学作用下发生张拉、剪切或拉剪破坏。对于岩土工程，可以用最大拉应变准则解决岩体破坏问题。借鉴已有研究成果，这里采用极限拉应变值确定隧道开挖后围岩松动圈范围。

岩石的极限拉应变可以通过岩石的单轴抗拉强度R拉与弹性模量E的比值确定：

在数值模拟中，通过ANSYS路径功能，在隧道顶部布置深度为20 m的参考线，等分为100段，计算相邻两测点的径向平均拉应变值ε

式中，δ为相邻两测点的相对位移；ΔL在本数值模拟中为0.2 m。计算判断松动区深度的表达式为：

(www.xing528.com)

在本例中，[ε]值的选取根据石吉线地质勘查报告（此处参照石吉线五峰山详细地质勘查报告，围岩情况与中龙隧道类似），并参考公路隧道设计规范围岩参数的选取范围[ε]=0.2‰。

通过反复调整围岩参数，使得计算得到的单洞隧道松动区范围与公路隧道规范中的松动区范围相符合，0°参考线方向极限拉应变与松动区深度的关系如图6-23所示。

图6-22　隧道顶部设置的参考线

图6-23　Ⅳ级围岩中0°参考线方向拉应变与围岩松动区深度关系曲线

图6-24　Ⅴ级围岩中0°参考线方向拉应变与围岩松动区深度关系曲线

通过数值模拟得到的Ⅳ级，Ⅴ级围岩松动区深度如表6-9所示。

表6-9　数值模拟得到的Ⅳ级，Ⅴ级围岩松动区深度

根据以上围岩松动区深度绘制出的松动区范围如图6-25、图6-26所示（其中红线为《公路隧道设计规范》给出的松动区范围，黑线为数值模拟的结果，可见二者是十分接近的）。

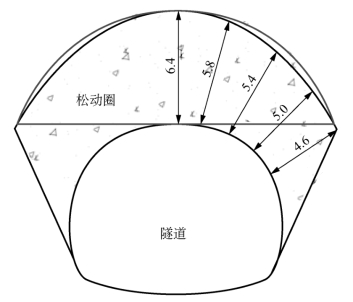
图6-25　Ⅳ级围岩松动区范围

图6-26　Ⅴ级围岩松动区范围

最终确定的围岩参数如表6-10所示：

表6-10　石吉中龙隧道围岩参数建议表

应该指出，围岩力学参数不是围岩的真实或者绝对的力学参数，由于岩土材料的复杂性，即使对于同一级别围岩，该值亦发生变化。这里将围岩力学参数设为定值，只是为了合理地减少设计变量，便于衬砌结构的优化。优化计算时选取Ⅴ级围岩计算。