拱顶沉降方法，地下结构最优

6.1.3.1　数值模拟

1.有限元模型基本假设

1）地表面和各土层呈均质水平层状分布；

2）初始地应力计算只考虑围岩自重应力，忽略岩体构造应力；

3）围岩是各向同性、连续的弹塑性材料，材料塑性屈服准则采用Mohr Coulomb屈服准则；

4）衬砌和锚杆视为弹性材料，根据混凝土和钢的弹性模量和泊松比计算单元刚度。

2.有限元模型

本次开挖模隧道埋深20 m。为了消除边界效应，底边及两侧距离隧道边界的最短距离取5倍隧道外径，即50 m，整个模型尺寸的X、Y方向尺寸为100 m×74.11 m。岩土层采用4节点平面应变单元，衬砌采用梁单元，锚杆采用杆单元。共计2 367个单元，2 696个节点。有限元模型如图6-4所示。

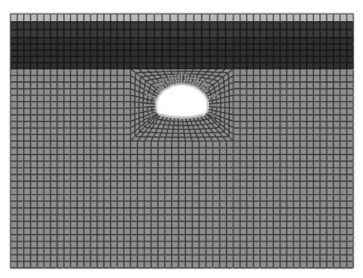
图6-4　有限元模型

3.有限元计算的Pyhton命令流

有限元计算程序，主要分成两个子程序。第一个是隧道建模程序，Tunnel_Function.py。该程序主要用来生成有限元模型。和GUI操作相同，主要分为六个模块，即部件，属性，装配，相互作用，荷载，网格（图6-5）。第二个是调用程序，tunnel_Optimization.py，主要用于提交分析和汇总结果。首先在JOB模块中提交计算，然后从ODB中提取出拱顶沉降数据存储在一个列表中。最后把列表中的数据写入Excel，便于数据的分析和处理。调用程序流程见图6-6。

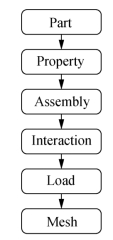
图6-5　有限元建模程序流程图

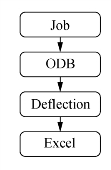
图6-6　调用程序流程

4.有限元计算过程

1）地应力平衡。

地应力平衡后的竖向应力云图如图6-7所示。模型底部约80 m，容重深度乘积验证，表明计算结果基本可靠。

图6-7　地应力平衡-竖向应力（k Pa）

地应力平衡后的竖向位移云图如图6-8所示。竖向位移最大值在10-5 m量级，而计算结果基本在0.1 m量级，地应力平衡结果理想。

2）开挖模拟。

土体同时施加衬砌，锚杆。开挖后的竖向变形云图如图6-9所示，因围岩弹性模量较小，约为50 MPa，最终变形值较大，最大沉降大于150 mm。

图6-8　地应力平衡-竖向位移力（m）

图6-9　开挖施工步-竖向变形云图（m）

3）结果输出。(www.xing528.com)

结果输出利用Python第三方库xlwt，将ABAQUS计算拱顶沉降结果列表写入一个Excel文件中。

6.1.3.2　数据分析

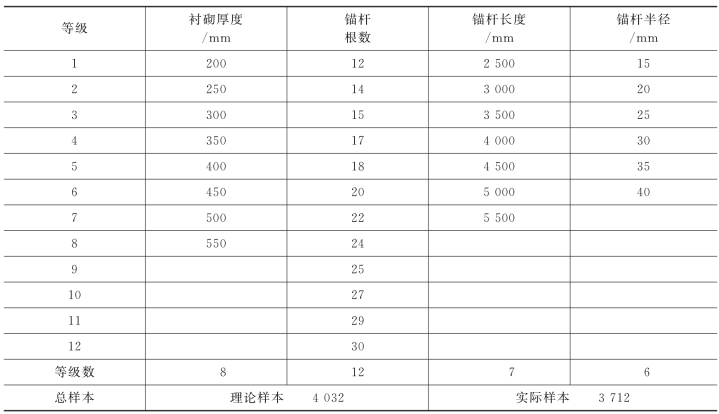
有了数值模型，我们将（t，n，l，r）输入ABAQUS中得到W，但优化过程中，每次都要调用ABAQUS模型来获得拱顶沉降，难度大，工作效率低，运算时间长。因此我们利用少量（W，t，n，l，r）数据，拟合出（t，n，l，r）和W之间的关系，这样在寻优过程中只需每次都调用该关系函数W（t，n，l，r），可以在保证精度的基础上，提高计算效率。通过正交试验的方法，让设计变量的不同水平互相组合，可以保证选取的样本的均匀性。衬砌厚度t取值范围为200～550 mm，每个水平增加50 mm，共8个水平；锚杆根数n取值范围为12～30，对应间距225～90 mm，每个水平增加一根，但数值模拟过程中特定锚杆根数的情况不收敛，无法得出沉降值，表中只列出了可以收敛的12个水平；锚杆长度l取值范围为2 500～5 500 mm，每个水平增加500 mm，共7个水平。锚杆半径r为15～40 mm，每个水平增加5 mm，共6个水平。这样理论上可以获得4 032个样本，但仍有一些情况不收敛，因此只得到了3 712个样本（表6-3）。

表6-3　选取样本时的设计变量水平

以（400，20，4 000，30）（衬砌厚度400 mm，锚杆20根，长度4 000 mm，半径30 mm）为基准点，每次改变其中一个变量，探讨各变量对拱顶沉降的影响（图6-10）。通过观察纵坐标的取值范围，可得衬砌厚度对拱顶沉降影响很大，而锚杆根数、长度、半径对拱顶沉降影响小。衬砌厚度与拱顶沉降之间的相关性极强，锚杆半径次之，而锚杆根数、长度与拱顶沉降之间的相关性较差。

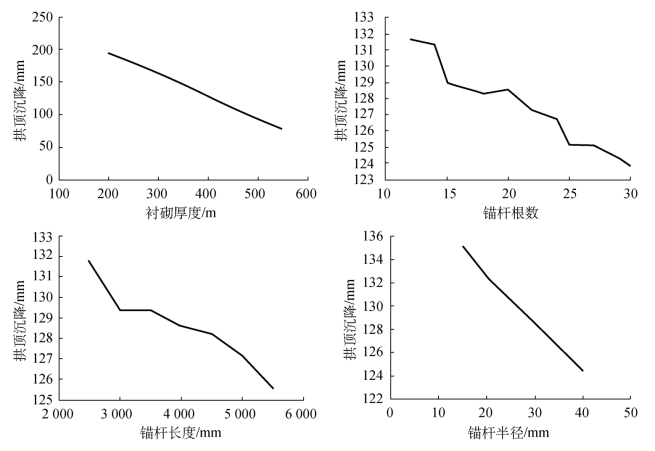
图6-10　各变量对拱顶沉降的影响曲线

通过多元线性回归分析可得W（t，n，l，r）（表6-4）

利用200个随机生成的样本进行效果检验，发现绝对误差平均值为1.34 mm，最大值为5.5 mm，相对误差平均值为1.12%，最大值5.95%，其精度不能令人满意。

表6-4　各变量与拱顶沉降的关系系数

将各变量的回归系数在其取值范围内归一化，得到的系数可以作为各变量对拱顶沉降的影响权重。衬砌厚度对拱顶沉降的影响很大，权重超过80%，而锚杆的三个因素对沉降的影响权重之和不到20%。

偏相关分析可以在分析两变量的相关关系时，剔除其他变量造成的影响。利用SPSS进行偏相关分析，可得设计变量与拱顶沉降间的偏相关性大小为：衬砌厚度＞锚杆半径＞锚杆根数＞锚杆长度。由于锚杆因素对拱顶沉降的影响很小，数值模拟不够精确问等题导致的拱顶沉降数值波动，造成了个别取值点处“锚杆支护增强不一定使得拱顶沉降减小”。

6.1.3.3　神经网络

利用3 712个学习样本训练神经网络，并利用随机生成的200个样本验证神经网络的预测效果。神经网络经过69次迭代终止学习，均方误差为1.2×10-4，没有达到目标值1.00×10-5（图6-11、图6-12）。有效性检验次数达到6次，意味着即使继续训练，也无法降低误差，提高预测精度。

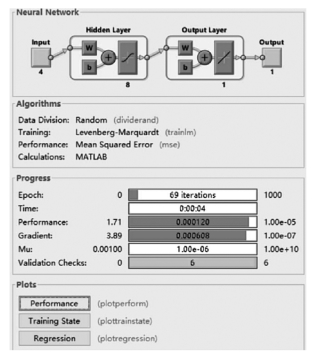
图6-11　神经网络训练结果

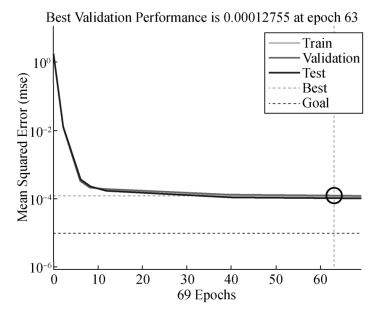
图6-12　均方误差收敛图

利用之前随机生成的200个样本验证神经网络预测效果（图6-13、表6-5），发现神经网络预测精度很高。

表6-5　神经网络预测效果验证

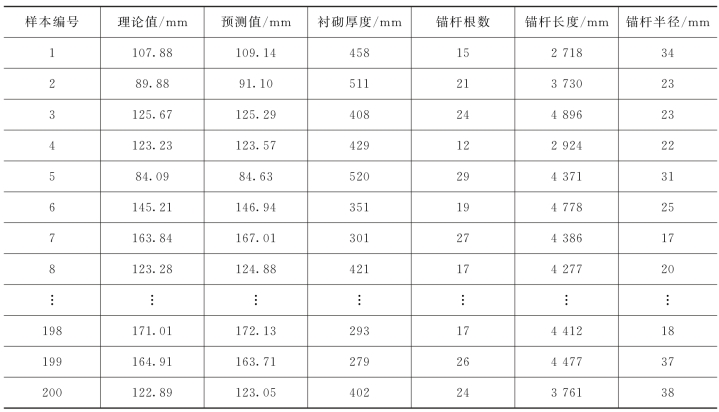
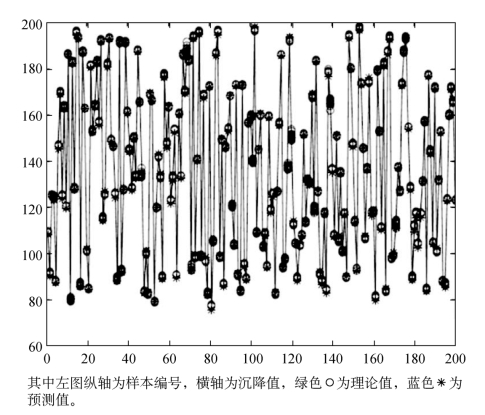
图6-13　神经网络效果验证

比较神经网络模型和多元线性回归的误差可发现（表6-6），应用神经网络模型对预测精度有明显的提升，相对误差平均值小于1%，最大值3%，绝对误差平均值小于1 mm，最大值2.89 mm。My_net函数即是W（t，n，l，r），我们不需要它的具体表达式，只需每次用sim（net，input）语句调用该函数，（t，n，l，r）输入前要做归一化操作，sim函数的输出经反归一化得到拱顶沉降的预测值。

表6-6　神经网络和线性回归比较