地下工程数学模型简化

MATLAB是一个数学软件，其强大的优化功能只能在已有明确的数学模型的基础上实现。而本问题是一个实际的工程问题，因而首先需要将其抽象为一个数学模型。

由于本模型采用地层——结构法计算，并且进行的是岩土体的弹塑性分析，因而是一个高度的非线性问题。从数学上来讲，其非线性主要表现在约束条件的高度非线性，即状态变量是设计变量的非线性函数，而这种非线性关系是无法给出显式表达式的。

利用有限元软件ANSYS进行数值计算，由优化工具箱的随机法（Random Designs）使设计变量在限制范围内随机变化20次，研究整个设计空间，并得到20组各状态变量和设计变量的对应数据。利用MATLAB内置拟合函数将各状态变量拟合为设计变量的3次齐次多项式，该多项式的项数表达式如下：

这样，该工程问题最终转化为的数学模型为：

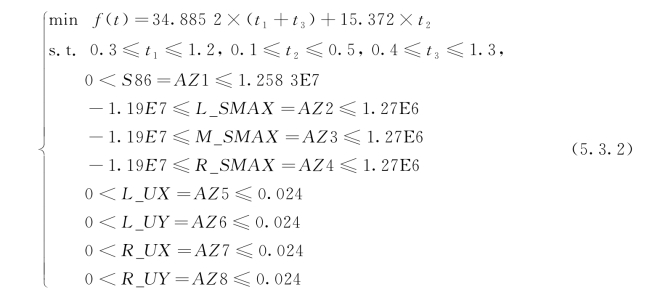
上式中：

f（t）——目标函数，单位米延长的衬砌总体积；

S 86——中隔墙最大MISES等效应力；

L_SMAX——隧道左洞衬砌最大应力；(www.xing528.com)

M_SMAX——隧道中导洞衬砌最大应力；

R_SMAX——隧道右洞衬砌最大应力；

L_UX——隧道左洞水平收敛；

L_UY——隧道左洞竖向收敛；

R_UX——隧道右洞水平收敛；

R_UY——隧道右洞竖向收敛。

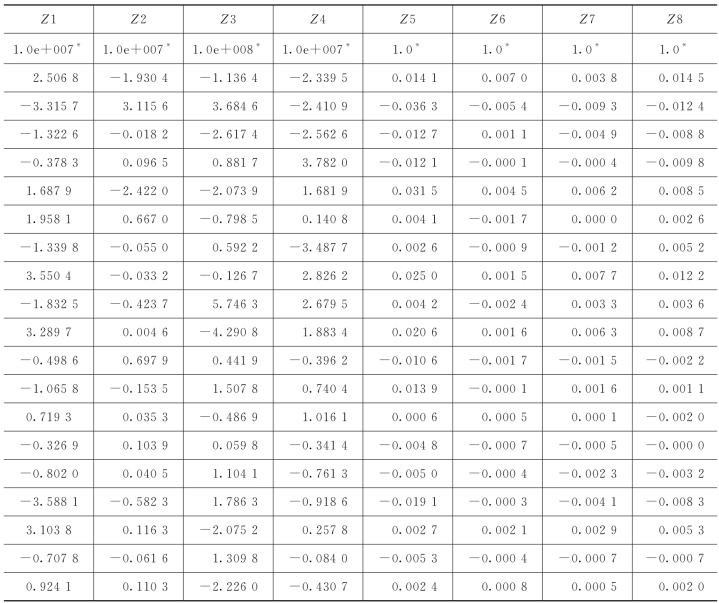
拟合得到的状态变量关于设计变量的系数矩阵见表5-11。

表5-11　由设计变量拟合状态变量的多项式系数矩阵