基于ANSYS的地下结构方法实例

本例以一整体式大跨浅埋隧道为例，来分析ANSYS优化算法在的地下结构优化方面的应用。隧道跨度19.96 m，高6.32 m，埋深20.00 m，围岩属强风化变余砂岩，稳定性差，结构破碎，划为V级围岩较为合适。

利用ANSYS进行建模，采用平面应变方法进行分析，DP模型（德鲁克-普拉格）屈服准则和相关流动准则来对隧道开挖过程进行分析。隧道二维平面应变模型如图5-24所示。模型两侧的水平距离为4倍隧道跨度，下边界至洞底距离为6倍洞高。上边界为自由面。两侧水平边界采用水平向约束，底部边界采用竖向约束。隧道采用上下台阶法施工，考虑支护作用。隧道支护的有限元网格如图5-25所示。

图5-24　有限元模型网格

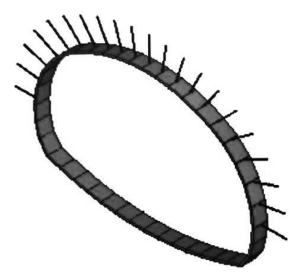
图5-25　支护结构网格

围岩采用实体四边形Plane42单元模拟，锚杆采用Link1单元模拟，初衬采用Beam3单元模拟。单元数共1 394个，具体计算参数如下表5-4所示。

表5-4　模型计算参数及取值

本例采用ANSYS零阶算法对隧道的锚杆截面和初衬厚度进行优化。设计变量（DV）为锚杆截面（RB）和初衬厚度（T）；状态变量为拱顶沉降（UY）、地表沉降（UY_FACE）、左右拱腰水平位移（UX1，UX2）以及隧道的最大等效应力（MAX_EQV）；目标函数DISP=1 000×（abs（UY+0.009）+abs（UX1-UX2））。图5-26为优化后的隧道竖向位移云。

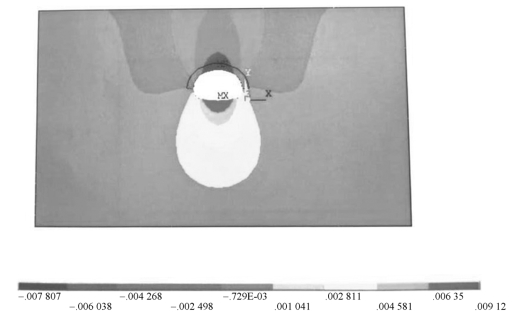
图5-26　优化后的隧道竖向位移云图

目标函数DISP，设计变量随迭代次数的关系曲线如图5-27—图5-29所示。

(www.xing528.com)

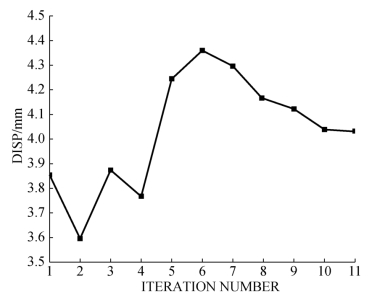
图5-27　DISP随迭代次数的关系曲线

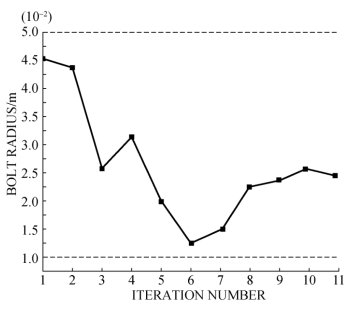
图5-28　锚杆半径随迭代次数的关系曲线

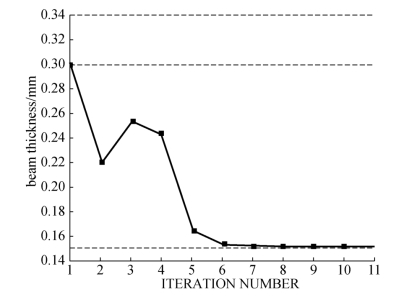
图5-29　衬砌厚度随迭代次数的关系曲线

本例采用三组不同的初值来考察零阶方法的适用性及优缺点。三组初值如表5-5所示，优化结构如表5-6、表5-7所示。

从图5-27可以看出，零阶方法的搜索范围很大，但它不容易得到全局最优解，往往得到的是局部最优解。从表5-3的结果可以看出，初始点的选择对优化结果影响很大，差异达到10%。

表5-5　设计变量初值

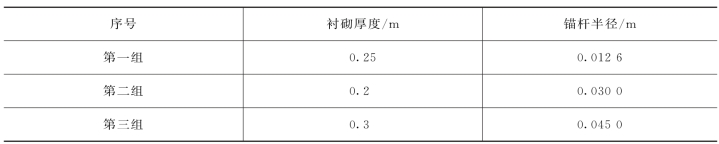
表5-6　优化结果（目标函数）

表5-7　优化结构（设计变量）

一阶方法是一种间接的方法，它需要对因变量球一阶导数，计算量大而费时。因此，对于不存在一阶偏导数的目标函数最优化问题以及大型复杂的非线性问题，一阶方法就显得有些无能为力。