地下结构竖向弹性地基梁解法

随着计算机的普及应用，数值解方法已成为地下连续墙等深基坑挡土结构的设计计算有效方法。其中弹性地基梁数值解法是此类方法中相当实用，且应用广泛的一种计算方法。

弹性地基梁数值解法又称为杆系有限元法，该方法实际上是矩阵位移法与弹性地基梁法的结合。该计算方法沿纵向取单位宽度的地下连续墙挡土结构，将其视为一个竖放的弹性地基梁。连续墙墙体根据要求剖分为若干段梁单元，支撑可用二力杆桁架单元模拟，地层对地下连续墙的约束作用可用一系列弹簧来模拟。弹簧的作用可按通常的弹性地基梁方法假定，即采用所谓的整体变形理论。

作用于地下连续墙墙背的主动土压力的大小和图形分布还随开挖面位置变化而变化。随着开挖面下移，主动土压力也随之增大。图2-6（a）～图2-6（d）分别表示了四种不同开挖深度时，作用于连续墙主动土压力值得变化过程。

弹性地基梁数值法可采用多种工况的计算简图，能反映地下连续墙荷载和内力随施工不同阶段的变化过程。图2-6表示设有三道支撑地下连续墙的四个阶段的受力状态。从图中可以看出作用于墙背的主动土压力（已扣除了基坑底面以下墙前静止土压力）是随着基坑开挖深度的增加而逐渐增加的。在具体应用弹性地基梁数值法计算时，有“全量法”和“增量法”两种方法的选择。图2-6实际上是设有三道支撑的地下墙的“全量法”计算图式。

所谓“全量法”是指对每一个施工工况，相应的主动土压力全部作用于支护结构上，求得的内力和位移即为该工况的实际内力和实际位移值。以图2-6（c）为例，这时处于地下连续墙的第二道支撑设置完成，且继续开挖下一层土方的施工阶段。墙上作用的荷载q3为该施工工况对应的全部主动土压力强度值。需要注意的是，先于第二道支撑设置，墙体已经发生了初始位移（初始位移值可由前一工况计算结果得到），安装新支撑杆时，杆端位置已经偏离了地下连续墙变形前的初始位置，但是这偏离值并不引起新支撑的轴力。计算时应该考虑这个因素，即应该对杆端的初始位移进行修正。这种修正当采用“全量法”时，点算程序处理较为困难，而改用“增量法”时要方便得多。所以工程中较多采用“增量法”。(www.xing528.com)

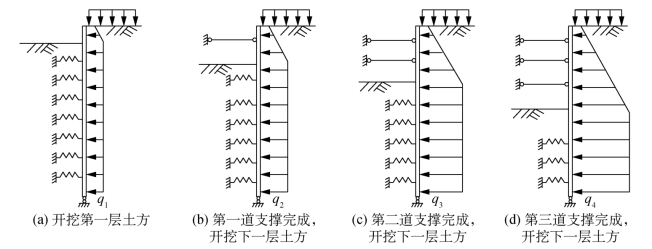
图2-6　三道支撑地下墙的计算简图（全量法）

“增量法”是将整个施工过程分成若干个工况，而将前后两个工况的荷载改变值称为荷载增量。由荷载增量引起的位移和内力称为位移增量和内力增量。累计从开始到当前施工阶段各工况的位移增量和内力增量，则可得到当前工况的实际位移和实际内力，图2-7为设置了三道支撑的地下连续墙的“增量法”计算简图。以图2-7（d）的第4个工况为例，墙体作用的增量荷载Δq4即为第3工况到第4工况之间的主动土压力增量，由此计算得到的位移和内力是加设第三道支撑后再挖土到基坑底面设计标高这个过程中新增加的位移和内力。如果需要知道作用在地下连续墙上的全部主动土压力，则可累加以前所有工况的荷载增量。图2-7（e）表示第4受力工况的全部主动土压力分布情况。q4为累计了前3个受力工况和当前第4个工况的荷载增量，其值与全量法计算简图2-6（d）中的q4相同。

图2-7　三道支撑地下墙的计算简图（增量法）