城市更新系统的结构构建：治理理论、实务与案例研究

城市发展问题是一类具有复杂非线性和动态反馈循环特征的系统决策优化过程，因此分析研究城市更新问题，必须用系统分析方法，从系统整体角度识别系统行为的运动规律。系统动力学以微分方程为其理论工具，关注系统整体及与系统相关的管理策略的行为趋势，适合用来深入探究城市更新系统的内部结构及其运行规律。

系统动力学著名的内生观点认为，系统的行为模式与特性主要取决于其内部的动态结构与反馈机制;系统在内外动力和制约因素的作用下按一定的规律发展。例如，城市旧城区旅游业的发展与其和旅游业相关的资源存在相互反馈的动态机制，旅游业的发展也需考虑相关资源之间的数量结构关系。因此，用系统动力学来分析城市更新问题，首先要描述和辨识城市更新系统的基本结构，在此基础上才能进一步探讨城市更新各相关系统结构与城市更新动态行为之间的内在关系。

(1)城市更新系统中的“因”“果”关系连接

系统动力学定义的系统是:一个由相互区别、相互作用的各部分有机地联结在一起，为同一目的而完成某种功能的集合体，即系统是由构成系统的基本单元(又称为“系统组分”)以及这些基本单元之间的关系联结所构成的。因此，可以认为系统的结构就是这些系统组分之间的关系的集合。要描述系统结构关系，首先要能描述这些系统组分之间的关系联结。这里，系统动力学提供了因果关系图示法来描述系统结构连接，它是一种比较形象化的方法。如图5-4所示，用一个由“原因”变量指向“结果”变量的有向箭头表示“连接”，以表达系统内部任何两个组分之间的因果关系。

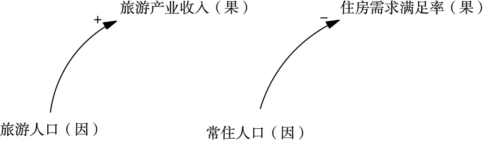
图5-4　系统连接

在图5-4中，箭头起点表示“原因”变量，箭头终点表示“结果”变量，“+”号表示由“原因”变量的增加导致“结果”变量的增加，是正相关关系，称为“同向”连接;“-”号表示“原因”变量的增加导致“结果”变量的减少，是负相关关系，称为“反向”连接。在实际系统中，“连接”所代表的数学关系表达式可能十分复杂，但总可以分成“同向”和“反向”两类最基本的连接关系，作为构成系统结构的最基本元素。例如，在城市生态经济子系统中，通过城市更新可吸引更多旅游人口，则将导致城市旅游产业收入增加;而常住人口的增加将会使住房需求满足率相对降低。

(2)城市更新系统的反馈回路与反馈系统

在系统中，由多个首尾相连的“连接”组成的无始无终的“闭合环”，表示这些因素之间存在某种反馈关系。对整个系统而言，“反馈”是指系统输出与来自外部环境的输入的关系。

反馈系统就是包含反馈环节与其作用的系统。它要受系统本身的历史行为的影响，把历史行为的后果回授给系统本身，以影响未来的行为。系统所包含的关系中只要存在一个反馈关系，该系统就被称为“反馈系统”或“闭环系统”。相反，不包含任何反馈关系的系统被称为“开环系统”。反馈系统形成闭合的回路，称为反馈回路。系统动力学是研究反馈系统的学科，因此系统动力学所研究的系统中至少包含一个反馈回路(图5-5)。例如，在城市更新中，加快住房建设速度将会增加旧城区现有的住房存量，使得住房需求满足率得到提升，从而反过来会抑制住房建设速度的提升。

图5-5中，反馈回路就是由一系列的因果与相互作用链组成的闭合回路或者说是由信息与动作构成的闭合路径。系统所包含的反馈回路一般不止一个，这些反馈回路互相连接与作用，从而构成了复杂的系统结构。反馈系统的结构就是相互联结与作用的一组回路。因此，系统动力学以反馈回路来描述系统的结构，把反馈回路作为系统的基本结构或基本单元。

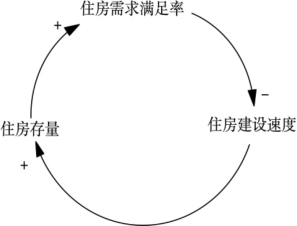
图5-5　系统反馈回路示意

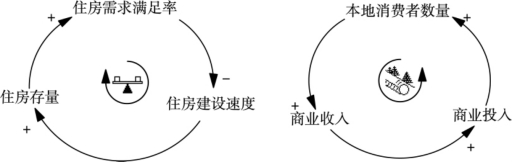
按照反馈过程的特点，反馈可划分为正反馈和负反馈两种。正反馈的特点是能产生自身运动的加强过程，在此过程中运动或动作所引起的后果将使原来的趋势得到加强;负反馈的特点是能自动寻求给定的目标，未达到(或者未趋近)目标时将不断作出响应。例如，城市更新中，加快住房建设速度将会增加旧城区现有的住房存量，使得住房需求满足率得到提升，从而反过来会抑制住房建设速度的提升，这种反馈为负反馈，它会使系统趋近平衡，如图5-6(左)所示;在商业开发中，商业收入的增加会带来商业投入的增加，从而吸引更多消费者，带来更多商业收入，这种反馈为正反馈，它会使系统得到加强，如图5-6(右)所示。

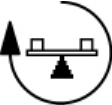具有正反馈特性的回路称为正反馈回路，用图式或者;具有负反馈特点的回路则称为负反馈回路，用图式或者。分别以上述两种回路起主导作用的系统则称之为正反馈系统与负反馈系统，如图5-6所示。

(www.xing528.com)

图5-6　负反馈回路和正反馈回路

(3)一阶反馈系统的分析与目标控制

系统动力学方法在城市更新政策优化与管理中的应用主要体现在对系统的管理控制上。通过研究系统的信息传递和控制调节问题，可以获得主要变量随时间变化的解析表达式，并确定如何对系统实施最优控制，使政策变量有效控制系统状态的发展变化。典型的一阶SD反馈回路模型如图5-7所示，它是建立城市更新整体模型的基础，对该简单模型的分析将应用到城市更新的整体SD模型中。

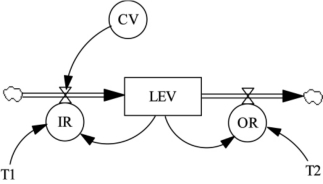
图5-7　一阶反馈循环回路模型

根据流图写出对系统状态进行控制的空间表达式，令:X=LEV U=CV。其中X为关于时间的导数，得到:

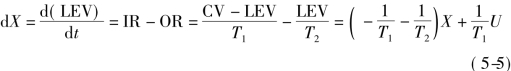
由此，可得系统的状态空间表达式为:X=AX+BU(5-6)

式中:A=-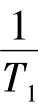-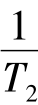;B=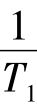

式(5-6)为线性定常系统非齐次方程，当系统的初始时刻为t=t0，初始状态为X(t0)时，该方程的解析解为:

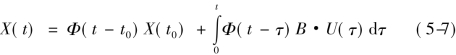
其中，Φ(t-τ)=e A(t-t0)。右端第一项始终表示由系统初始状态引起的自由运动，第二项表示由控制激励作用引起的强制运动(若为齐次方程，则不存在第二项)。对式(5-7)，设t0=0，并假定U=CV为不随时间变化的常数值，则:

例如，在分析旧城区房地产再开发项目决策方案时，住房存量面积的变化=住房面积增量-住房面积减量;同时，住房面积存量对住房面积增量有较大影响，住房面积增量=(住房面积存量×住房面积增长率)/时间，如图5-8所示。同理，此方法还可拓展用于城市更新过程中的其他项目方案决策中。

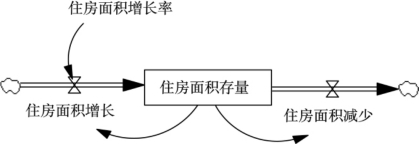
图5-8　房地产开发反馈循环回路