系统安全性的评价-系统可靠性与安全性

波兰学者Pawlak.Z.1982年提出的粗糙集（Rough Set）理论是一种研究不完整、不确定知识的表达、学习及归纳的数学方法。它为研究不精确数据和不完整数据的分析、推理，挖掘数据之间的关系，发现潜在的知识提供了行之有效的工具。该方法计算简单，完全从数据中分析各个预测方法的重要程度，克服了一些专家评估方法的主观性，使得综合评估更具客观性。

1.不可分辨关系

粗集理论认为知识是与分类紧密联系在一起的，知识是基于对象分类的能力，分类的过程就是将相差不大的对象分为一类，它们的关系就是不可分辨关系也称等价关系。知识库可表示为K＝（U，R）。其中U为非空有限集称为论域，R是U上的一族等价关系。U /R为R的所有等价类族。[X]R表示包含元素x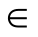U的R的等价类。若PR且P≠，则P中全部等价关系的交集也是一种等价关系，称为P上的不可分辨关系，记ind（P），。

2.粗集的近似及边界

粗集对不精确概念通过上近似和下近似两个精确集来表示。给定知识库K＝（U，R），对于每个子集xU和一个等价关系Rind（K），定义两个子集：

分别称R-（X）、R-（X）为X的R下近似集和R上近似集，集合X的R边界域定义为

bnR(X)＝R-(X)-R-(X)

同时，定义posR（X）＝R-（X）为X的R正域；negR（X）＝U-R-（X）为X的R负域。(www.xing528.com)

3.信息系统与决策表

知识表达系统也称为信息系统，是用关系表的形式表达的。具有条件属性和决策属性的知识表达系统就是决策表。决策表是一类特殊而重要的知识表达系统。设S＝（U，A，V，f）为知识表达系统。其中：S＝（x1，x2，…，xn）是对象的有限集合；A＝（a1，a2，…，an）为属性的有限集合；V为属性A所构成的域；f：U×A →V为一个信息函数，U中任一元素取属性a在V中有唯一确定值，A＝C∪D，C为条件属性的集合；D为决策属性的集合。

4.决策表的简化

决策表的简化就是化简决策表中的条件属性，化简后的决策表具有与化简前的决策表相同的功能，但是化简后的决策表具有更少的条件属性。因此，决策表的简化在实际应用中相当重要，同样的决策可以基于更少量的条件，使我们通过一些简单的手段就能获得同样要求的结果。决策表的简化步骤如下：

（1）进行条件属性的简化，即从决策表中消去某些列；

（2）消去重复的行；

（3）消去属性的冗余值。