系统可靠性与安全性的多维联系数评价

由于多维联系数是一个新生事物，国内外还没有学者对它进行系统研究。应用系统科学思想、利用不确定性数学方法，在界定多维联系数定义的基础上，研究其运算和算法，并建立基于多维联系数的综合评价模型。

1.多维联系数的界定

当利用n个指标i1，i2，…，in对某一事物或现象进行测度时，如果测度指标间满足偏好独立性条件，则总体效用函数是相加性的。所以，这时把n个指标看成n个维度，用一个效用函数表示为

其中　——n个指标代表的维数（n=1，2，3，…）；

c1，c2，…，cnR——相应指标的考察值。

则把效用函数称为n维联系数，即多维联系数。

例如，当有4个指标时，多维联系数为

当有3个指标时，多维联系数为

2.基于多维联系数的测度模型

对于一个多指标的综合测度问题，设测度事物或现象的方案集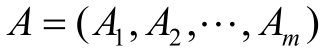，测度指标集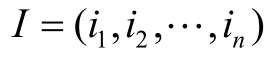，且指标集的权重向量，其中。

利用指标集对方案Ai进行考察时，其考察值为，决策矩阵

由于各指标的含义不同，指标值的计算方法也不同，造成各个指标的量纲各异。因此，即使各指标定量化了，也不能直接进行计算，必须先对指标进行标准化处理。所以，为了使各指标有公度性，通过构造关联函数将各指标进行标准化处理。

当ii为效益型指标时：

当ii为成本型指标时：

则标准化矩阵

根据式（7.1）、（7.2）将决策矩阵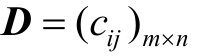转化为标准化矩阵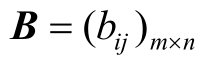；再根据式，将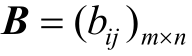转化为n维联系数决策矩阵，则

所以，基于多维联系数的测度模型的计算过程如下：

步骤一，确定指标的权重向量W＝（w1，w2，…，wm）T。

权重系数应当是各个指标在指标总体中的变异程度和对其他指标的影响程度的度量，赋权的原始信息应当直接来源于客观环境，可根据各指标所提供的信息量的大小来决定相应指标的权重系数。具体方法如下：

（1）计算第j个指标在第i个方案所占的比重

其中　xij——标准化处理后的计算值。(www.xing528.com)

（2）计算第j个指标的熵值。

（3）计算第j个指标的差异系数gj＝1-ej。

（4）计算第j个指标的权重。

故指标Ii的权重系数

步骤二，确定每个指标的绝对理想解和绝对负理想解。

定义指标的理想解和负理想解分别表示为

正理想解：

其中，。

负理想解：

其中，。

因此，指标的绝对理想解为

绝对负理想解为

步骤三，利用海明距离计算各决策方案到绝对理想解的距离。

则

步骤四，利用海明距离计算各决策方案到绝对负理想解的距离。

令

则

步骤五，根据各决策方案到绝对理想解的距离和到负理想解的距离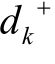-，计算综合测度指数pk（k＝1，2，…，m ）；根据pk对各决策方案进行排序和择优，pk越大，则方案越优。

pk的计算公式为