基于价值函数的综合评价在系统可靠性与安全性中的成果

对于一个多指标多目标的综合测度问题，设测度的方案集A＝{A1，A2，…，Am}，测度指标集X＝{x1，x2，…，xn}，决策矩阵D＝{dij}，其中i＝1，2，…，m；j＝1，2，…，n。

价值函数就是多指标多目标决策问题的效用函数。一般在决策矩阵D上的效用函数为线性函数或指数函数，如果测度指标间满足偏好独立性条件，则总体价值函数是相加性的，即

其中　wj——多指标的加权系数。

根据系统的特征，选用指数形式的价值函数组合指标价值函数。设xj的价值函数

其中　C，B——待定常数；

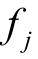——xj的值域集合到值域[0，1]的映射函数。

1.确定价值函数的值

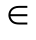由于测度指标的计算方法和含义不同，所以它们属于不同类型指标。通常测度指标有：效益型、成本型和固定型。所以，记I1为效益型指标集合，I2为成本型指标集合，I3为固定型指标集合。令，其中rj为固定指标值（xjI3），取

系数C，B属已知价值函数形式的特定参数，可通过参数特征（最大值、中间值、最小值的效用）求出，这时价值函数就可唯一求得。(www.xing528.com)

其中，为最优指标效用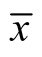，为中值指标效用。

2.利用相对比较法确定测度指标权重系数

相对比较法是将所有测度指标分别按行和列排列，构成一个正方形的表，再根据三级比例标度对任意两个指标的相对重要关系进行分析，并将评分值记入表中相应位置；将各个指标评分值按行求和，得到各个指标的评分总和；最后做归一化处理，得到指标的权重系数。

三级比例标度两两相对比较评分的分值为qij，则标度值

则评分构成的矩阵

其中，qii＝0.5，qij+qji＝1。

则指标xi的权重系数