事故树分析法（Accident Tree Analysis，ATA）又称故障树分析法，是安全系统工程的重要分析方法之一，是一种演绎的安全系统分析方法。事故树分析法是从要分析的特定事故或故障（顶上事件）开始，层层分析其发生原因，直到找出事故的基本原因（底事件）为止。这些底事件又称基本事件，它们的数据已知或者已经有统计或实验的结果。
1.事故树分析的特点
事故树分析是一种演绎推理法，各种原因之间的逻辑关系用一种称为事故树的树形图表示（顶事件、中间事件、底事件、逻辑符号），可作定性与定量分析。事故树分析是一种图形演绎方法，便于找出系统的薄弱环节，具有很大的灵活性，是一个对系统更深入认识的过程，可以定量计算复杂系统发生事故的概率。事故树组成的例子如图7.11所示。
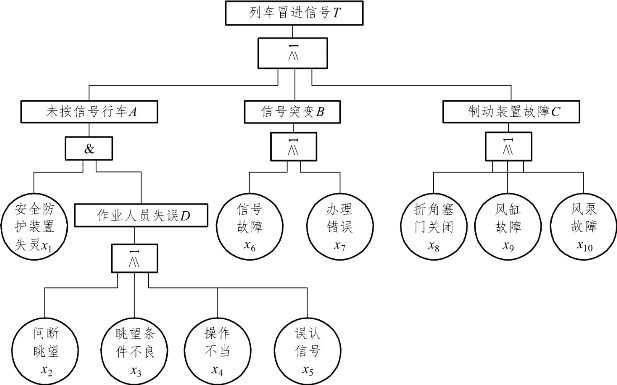
图7.11 事故树的组成
2.事故树分析的步骤
事故树分析主要有四步：
（1）准备阶段。确定所要分析的系统、熟悉系统、调查系统发生的事故。
（2）事故树的编制。确定事故树的顶事件、调查与顶事件有关的所有原因事件、编制事故树。
（3）事故树定性分析。
（4）事故树定量计算。
3.事故树的符号及其意义
（1）事件及事件符号。事件主要包括结果事件、底事件和特殊事件。
结果事件：用矩形符号表示，分为顶事件和中间事件。
底事件：导致其他事件的原因事件，底事件又分为基本原因事件（圆形符号）和省略事件（菱形符号）；
特殊事件：表明其特殊性或引起注意的事件，特殊事件又分为开关事件（房形符号）和条件事件（椭圆形符号）。特殊事件符号如图7.12所示。
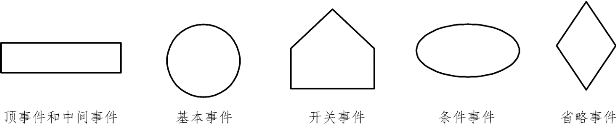
图7.12 特殊事件符号
（2）逻辑门及其符号。逻辑门是连接各事件并表示其逻辑关系的符号，主要有与门、或门、特殊门、条件与门、条件或门等。逻辑门符号如图7.13所示。
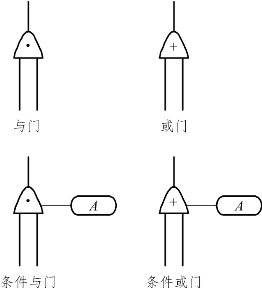
图7.13 逻辑门符号
（3）转移符号。转出符号是表示向其他部分转出的符号，△内记入向何处转出的标记；转入符号是表示从其他部分转入△，△内记入从何处转入的标记。转移符号如图7.14所示。
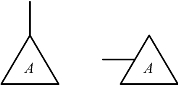
图7.14 转移符号
4.事故树的编制
事故树的编制是事故树分析中最基本、最关键的环节。事故树的编制目的：通过编制过程发现系统中的薄弱环节。事故树的编制人员应由系统设计人员、操作人员和可靠性分析人员组成。
（1）事故树的编制过程应遵循的规则。事故树的编制过程是一个严密的逻辑推理过程，应遵循以下规则：确定顶事件应优先考虑风险大的事故事件；合理确定边界条件；确切描述顶事件；保持门的完整性，不允许门与门直接相连；及时进行合理的简化；对编制的事故树反复进行合理性检验。
（2）编制事故树的方法。编制事故树的常用方法为演绎法：确定系统的顶事件，找出直接导致事件发生的各种可能因素或因素的组合即中间事件；在顶事件与其紧连的中间事件之间，根据其逻辑关系相应地画上逻辑门；对每个中间事件进行类似的分析，找出其直接原因，逐级向下演绎，直到不能分析的基本事件为止。
5.事故树的定性分析
事故树的定性分析主要有：事故树的割集与最小割集、事故树的径集与最小径集、根据最小割集和最小径集预测事故树的薄弱环节。定性分析步骤有：
（1）割集与最小割集。
割集：在事故树分析中，引起顶事件发生的基本事件的集合称为割集，也称截集或截止集。
最小割集：一个事故树中的割集一般不止一个，在这些割集中，凡不包含其他割集的，叫作最小割集。最小割集是引起顶事件发生的充要条件。
（2）最小割集的求法。
最小割集的求法有多种，布尔代数法最为简单，应用较为普遍。布尔代数也叫逻辑代数，逻辑代数的运算法则很多，有的和代数运算法则一致，有的不一致。它主要有交换律、结合律、分配律、等幂律、吸收律等。根据求得的最小割集，可画出事故树的等效树。
（3）利用布尔代数求最小割集，并画出等效树。
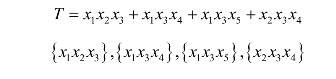
等效树如图7.15所示。
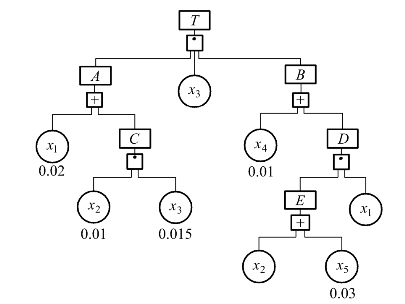
图7.15 等效树图
（4）求解径集与最小径集。
径集：在事故树中，使顶事件不发生的基本事件的集合称为径集，也称通集或路集。(www.xing528.com)
最小径集：如果径集中任意去掉一个基本事件后就不再是径集，那么该径集就是最小径集。最小径集是保证顶事件不发生的充要条件。
（5）最小径集的求法。
将原来事故树中的逻辑与门改成逻辑或门，将逻辑或门改为逻辑与门。
根据对偶原理，事故树的对偶树是成功树，成功树是顶事件不发生的树；将事故树变换成其对偶的成功树，然后求出成功树的最小割集，即是事故树的最小径集。
（6）最小割集/最小径集在事故树分析中的作用。
最小割集的作用主要有四个方面：表示系统的危险性，最小割集越多，说明系统的危险性越大；表示顶事件发生的原因组合；为降低系统的危险性提出控制方向和预防措施；利用最小割集可以判定事故树中基本事件的结构重要度和计算顶事件发生的概率。
最小径集的作用主要有三个方面：表示系统的安全性，最小径集越多，说明系统安全性越高；选取确保系统安全的最佳方案；利用最小径集可以判定事故树中基本事件的结构重要度和计算顶事件发生的概率。
6.事故树的定量分析
事故树的定量分析主要是：确定基本事件的发生概率；求出事故树顶事件的发生概率；与系统安全目标值进行比较和评价。
事故树定量计算时的基本假设：基本事件之间相互独立；基本事件和顶事件都只考虑发生和不发生两种状态；假定故障分布为指数函数分布。定量分析具体步骤有：
（1）基本事件的发生概率。
它包括系统的单元故障概率及人的失误概率等。在工程计算时，常用基本事件发生的频率来代替其概率值。确定方法有经验法、专家咨询法。
（2）顶上事件发生概率的计算。
已知基本事件的发生概率，各基本事件是独立事件，相对简单的计算方法是最小割集法，事故树如图7.11所示。
精确计算是基本事件的相互独立特性，近似计算是将基本事件之间的相互独立关系看作相互排斥关系。
因为
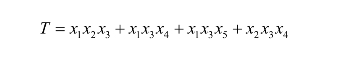
所以
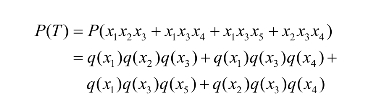
7.基本事件的重要度分析
重要度的含义：事故树中各基本事件的发生对顶事件的发生影响程度的大小。
影响重要度大小的两个因素：各基本事件发生概率的大小；各基本事件在事故树模型结构中处于何种位置。
基本事件的重要度分析主要有：基本事件的结构重要度；基本事件的概率重要度；基本事件的临界重要度。
（1）基本事件的结构重要度。假定基本事件发生概率相等，从事故树的结构上研究各基本事件对顶事件的影响程度。确定方法有两种：①精确计算出结构重要度系数；②按结构重要度进行排序。
（2）基本事件的概率重要度。结构重要度分析的不足：没有考虑基本事件发生概率的变化对顶上事件发生概率的影响。基本事件的概率重要度系数：指某基本事件发生概率的变化引起顶事件发生概率变化的程度。
（3）基本事件的临界重要度。一般来说，减少概率小的事件的概率比减少概率大的基本事件的概率困难，但概率重要度系数不能反映这一实际情况。因而它不能从本质上准确地反映出各基本事件在事故树中的重要程度。而临界重度系数，是指某个基本事件发生概率的变换率引起顶事件发生概率的变化率，它是从敏感度和概率双重角度衡量各基本事件的重要程度。因此，它比概率重要度更合理更具有实际意义。临界重要度系数为
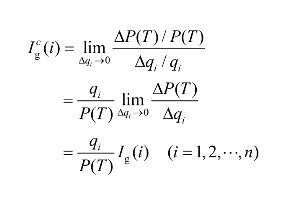
式中 P（T）——顶事件发生概率；
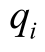——第i个基本事件xi的发生概率；
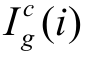——第i个基本事件xi的临界重要度系数；
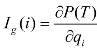——第i个基本事件xi的概率重要度系数。
若所有基本事件的发生概率都等于0.5，则基本事件的概率重要度系数等于其结构重要度系数。
【例7.2】 如图7.16所示，事故树的最小割集为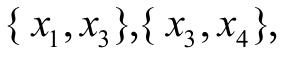
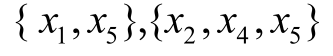，各基本事件的发生概率分别为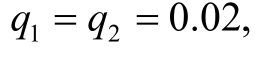
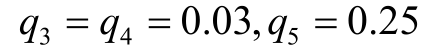。求各基本事件的概率重要度系数。
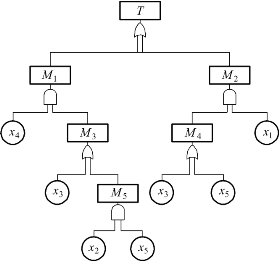
图7.16 事故树图
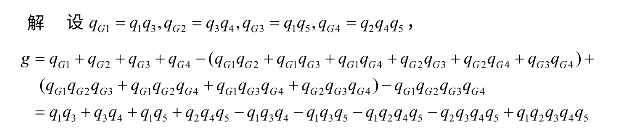
分别求偏导，得
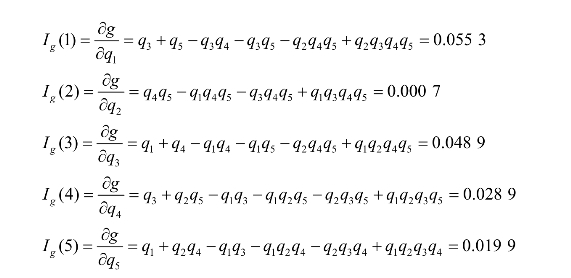
（4）三种重要度系数的对比。
结构重要度系数：从事故树结构上反映基本事件的重要程度，反映某一基本事件在事故树结构中所占的地位。
概率重要度系数：反映基本事件概率的增减对顶事件发生概率影响的敏感度，起着一种过度作用，是计算两种重要度系数的基础。
临界重要度系数：从敏感度和自身发生概率大小双重角度反映基本事件的重要程度，从结构及概率上反映改善某一基本事件的难易程度。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
