系统可靠性与安全性分配方法

将系统需要达到的可靠性水平，相等地分配到各子系统，这种方法称为可靠度分配法，也称均衡分配法。分配中不考虑成本、失效率、安全性等实际情况，以统一标准分配可靠度。目前可靠性的分配方法有：

（1）无约束分配法（Unconstrained Distribution Method）：等可靠性分配法、再分配法、等系统失效率预计值法、考虑重要度和复杂度的分配方法。

（2）有约束分配法（constrained Distribution Method）：拉格朗日乘数法、动态规划法、直接寻查法。

1.无约束分配法——等分配法（Equal Distribution Method）

对系统中的全部单元配以相等的可靠度的方法。

（1）串联系统的等可靠度分配法。串联系统可靠度分配：串联系统的可靠度取决于系统中的最弱单元，当系统中的n个单元具有近似的复杂程度、重要性以及制造成本时，可用等分配法分配系统各单元的可靠度。基于这种考虑，各子系统应取相同的可靠度进行分配。对于串联系统，为使系统达到规定的可靠度水平　sR，各子系统也应具有相当的可靠性水平，其关系式为

【例5.2】　一台汽车保修设备，由四部分串联组成，要求总体可靠度达到Rs＝0.92，其中已知某一部分的可靠度为0.98，按等可靠度分配法确定其余三部分的可靠度。

解　设已知的可靠度R1＝0.98，其余部分的可靠度为R0，按照串联系统的等可靠度分配法的计算公式，有

所以，其余部分的可靠度为

因此，其余3部分的可靠度为0.979 1。

（2）并联系统的等可靠性分配法。并联系统可靠度分配：当系统的可靠度要求很高，而选用的单元又不能满足要求时，可选用n个相同单元并联起来。并联系统的等可靠度分配法的公式为

并联系统的等可靠度为

式中　Fs——系统要求的不可靠度；

Fi——第i个单元分配到的不可靠度；

Rs——系统要求的可靠度；

n——并联单元数。

【例5.3】　由三个单元组成的并联系统，要求系统可靠度达到0.95，求每个单元的可靠度。

解　已知Rs＝0.98，设每个单元的可靠度为R0，则

计算可得

等可靠度分配法的优点是比较简单；其缺点是没有考虑各子系统的重要性、成本高低、修复的难易程度、现有可靠性水平等。

2.无约束分配法——再分配法（Redistribution Method）

利用等分配法对串并联系统进行可靠度分配，可先将串并联系统简化为等效的串联系统和等效单元，再给同级等效单元分配相同的可靠度。串联系统中，可靠性越低的单元越容易改进。所以，把原来可靠性较低的单元的可靠度全部提高到某个值，而原来可靠度较高的单元的可靠度则保持不变。

通过计算得到各分系统的可靠度R1，R2，…，Rn，则系统可靠度为

式中　i＝1，2，…，n ——分系统数量。

如果　Rs﹤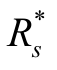（规定的可靠性指标），即所设计的系统不能满足规定的可靠度字表的要求，那么就需要进一步改进原设计以提高其可靠度，也就是要求对各分系统的可靠性指标进行再分配。可靠度的再分配就是用来解决这个问题的。根据以往的经验，可靠性越低的分系统（或元部件）改进起来越容易，反之越困难。可靠度再分配法的基本思想是把原来可靠性较低的分系统的可靠度全部提高到某个值，而原来可靠度较高的分系统的可靠性仍保持不变。其具体步骤如下：

（1）根据各分系统的可靠度的大小，由低到高依次排列为

（2）按可靠度再分配法的基本思想，把较低的可靠度　R1，R2，…，Rk0都提高到某个值R0，而原来较高的可靠度　Rk0+1…Rn保持不变，则系统可靠度为

（3）确定k0和R0，也就是要确定哪些分系统的可靠度需要提高，以及提高到什么程度。k0可以通过下面不等式求得

令　Rn+1＝1

k0就是满足不等式（5.7）的j的最大值：

【例5.4】　一个系统由3个分系统串联而成，预计它们的可靠性分别为0.7、0.8和0.9，则系统可靠度Rs＝0.504，规定的系统可靠度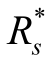＝0.68。试着对3个分系统进行可靠度再分配。

解　已知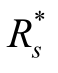＝0.68，n＝3，则原分系统的可靠度由低到高依次排列为

R1＝0.7,R2＝0.8,R3＝0.9

按公式（5.8）确定k0，由公式（5.5）可得到　Rn+1＝R4＝1。则

当j＝1时，

当j＝2时，

当j＝3时，

k0是满足公式（5.8）的j的最大值，因此k0＝2。确定R0：

得到R1＝R2＝R0＝0.85，R3＝0.9，即第一个、第二个分系统的可靠度均提　高到0.85，而第三个分系统的可靠度保持不变。系统可靠度　Rs按照公式（5.6）算出：

经过可靠度再分配后，新系统满足了规定的可靠度指标。

3.无约束分配法——相对失效率分配法（Relative Failure Rate Distribution Method）

以预测（即原有）失效率为依据，将分配于各子系统的（容许）失效率正比于预测（原有）失效率，这种分配方法称为相对失效率分配法。相对失效率分配法的基本思想是根据相对失效率分配方法的原则，分配于各子系统的（容许）失效率大小，与预测失效率有很大关系。预测的失效率越大，分配给它的失效率也越大；反之，可靠性越高的产品，分配的（容许）失效率也越小。这种分配方法，通常适用于失效率为常数的单元组成的串联系统，单元和系统的寿命均服从指数分布，分配过程中依照失效率作分配。

分配思想：可靠性模型正确、预计方法统一、数据相对关系正确，那么可靠性预计结果基本能反映出系统各组成单元之间的复杂程度、技术难易程度、可靠性水平。它适用于系统设计阶段的可靠性分配。(www.xing528.com)

设系统由n个子系统串联而成，它们分配到的失效率分别为λ1，λ2，∙∙∙，λn。系统失效率目标值为λs，分配的结果满足：

可靠性分配的目标是确定λi。具体步骤如下：

（1）根据现有的可靠性数据资料，推测（或已知）原各子系统的失效率，假设分别为di（i＝1，2，…，n）。

（2）计算各子系统的失效率ωi。

式中，分配系数ωi为相对失效率。

（3）计算分配于各子系统的容许失效率λi。

（4）检验分配结果是否满足下式：

（5）计算各子系统的可靠度Ri（t）。

为满足可靠度分配值之和大于系统可靠度目标值，各子系统的可靠度应当满足以下关系式：

【例5.5】　已知一个串联系统由4个子系统组成，预测的各子系统失效率分别为

要求系统的可靠度达到0.90，保证连续工作60 h以上。试用相对失效率法进行可靠度分配。

解　由已知条件得到

计算失效率分配系数：

同理得

计算各子系统的失效率：

由题意可知，Rs（60）＝0.85，假设系统的失效率为常数λs，则

各子系统的（容许）失效率为

计算各子系统所得的可靠度：

4.无约束分配法——加权修正分配法（Weighted Modified Distribution Method）

组成系统的各单元（含子系统、总成、部件），在系统中的重要程度是不同的，反映其重要程度的指标就是重要度。这种方法适用于各单元工作期间失效率为常数的串联系统。

根据各单元重要度分配给不同的可靠度，这种可靠性分配的方法，称为加权修正分配法，也称AGREE分配法（Advisory Group on Reliability of Electronic Equipment）。

单元的重要度就是该单元失效引起系统失效的次数与该单元失效次数的比值，它的意义是第i个单元失效造成系统发生故障而不能运行的概率，记作Wi。

（1）重要度（Importance Degree）。重要度是指某个单元发生故障时对系统可靠性的影响程度，一般用Wi表示：

式中　N——由第i个单元故障引起的系统故障次数；

ri——第i个单元的故障总次数。

串联系统中每个单元的每次故障都会引起系统发生故障，所以每个单元对系统的重要度都是相同的，即Wi＝1。

对于冗余系统0﹤Wi﹤1，Wi大的单元分配到的可靠性指标应该高一些。

（2）复杂度（Order of Complexity）。复杂度是指某个单元的元器件数与系统总元器件数之比，一般用Ki表示：

式中　ni——第i个单元的重要零、部件总数；

N——系统的重要零、部件总数，且

复杂度Ki大的单元，由于包括的元器件数量多，较复杂，实现较高的可靠性指标困难，故分配的可靠性指标应低一些。单元失效率与系统失效率的比值与该单元的重要度成反比，与该单元的复杂度成正比。

加权修正分配法适用于指数分布的串联系统，比前几种分配方法较为完善，其中考虑了单元的复杂程度、单元失效与系统失效之间的关系。加权修正分配法按串联系统的组合形式进行分析，且认为各分系统的寿命时间均服从指数分布（失效率与时间无关）。加权修正分配法的计算步骤如下：

（1）按等可靠度分配法初定失效率（即在等分配的基础上考虑重要度）。若规定系统工作到时间T时，应具有的可靠度（指标值）为Rs（T），在不考虑重要度时，单元容可靠应满足：

根据等可靠度分配法，通过公式推导求得

结合式（5.9）、（5.10），得单元容许失效率λi：

（2）对初定失效率进行重要度加权修正处理：

考虑复杂性后的加权处理。假设单元是由Ni个重要零件组成，系统的重要零件总数为。若这些重要零件的可靠性对系统的影响是相同的，则单元所包含的重要零件数占系统总的重要零件数的比率，就表示单元的复杂度。

再一次对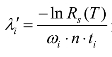进行复杂度加权处理，即将式（5.11）中的用代替，单元复杂度高，对允许失效率适当放宽，于是得到公式：

5.约束分配法——拉格朗日乘数法（Lagrange Multiplier Approach）

拉格朗日乘数法适用于在优化设计的条件下，解决可靠性设计中最关键也最实际的问题，即在保证产品可靠性总指标的分配，又能实现总的成本最小。

在数学最优问题中，拉格朗日乘数法（以数学家约瑟夫·路易斯·拉格朗日命名）是一种寻找变量受一个或多个条件所限制的多元函数的极值的方法。这种方法将一个有n个变量与k个约束条件的最优化问题转换为一个有n+k个变量的方程组的极值问题，其变量不受任何约束。这种方法引入一种新的标量未知数，即拉格朗日乘数：约束方程的梯度（Gradient）的线性组合里每个向量的系数。此方法的证明要用到偏微分、全微分或链法，从而找到能让设计出的隐函数的微分为零的未知数的值。

拉格朗日乘数法是一种将约束最优化问题转换为无约束最优化问题的求优方法，由于引入待定系数——拉格朗日乘子，则可利用这种乘子将原约束最优化问题的目标函数和约束条件组合成一个称为拉格朗日函数的新目标函数，使新目标函数的无约束最优解就是原目标函数的约束最优解。