系统可靠性预计方法-系统可靠性与安全性

系统可靠性预计是可靠性设计的重要任务之一，它在系统设计的各阶段（如方案论证、初步设计及详细设计阶段）要反复进行。根据设计任务书要求，预计基本可靠性或任务可靠性。将预计值和要求值相比较，当预计结果不能满足其规定要求时，应改进设计来满足系统可靠性指标。

1.数学均分法（Mathematical Equable Method）

数学均分法就是依据组成系统的各单元间的可靠数学模型，按概率运算法则，预计系统可靠度的一种方法，是一种经典的方法。工程上，其具体步骤是：建立系统的可靠性逻辑框图及可靠性数学公式，并利用相应的公式，依据已知条件求出系统的可靠度。

若基本可靠性模型为串联模型，设系统各组成单元之间相互独立，则系统可靠性为

式中　Ri（ti）——第i个单元可靠度；

ts——系统工作时间；

ti——第i个单元工作时间。

严格地说，系统内各组成单元的工作时间并非一致。工程上为简单起见，将系统内各单元工作时间视为相等，各单元工作时间视为相等，且各单元均服从指数分布，即设：

式中，λi为第i个单元故障率。

各单元均服从指数分布，则系统的可靠度为

因各单元均服从指数分布，且为串联模型，则系统必然也服从指数分布，

即

由此可得系统的故障率：

式中，λi为第i个分系统的故障率。

对于串联模型，预计其系统的故障率等于各单元故障率之和。另外，若系统中有部分单元工作时间少于系统工作时间，则根据公式（5.1）预计的结果一定是偏保守的。数学模型法的优点是计算比较精确，缺点是比较麻烦，且需要画出系统的逻辑图。

2.上、下限法（Upper and Lower Limit Method）

上、下限法又称边值边。对于一个复杂的系统，采用数学模型法很难得到可靠性函数表达式，此时忽略一些次要因素，用近似的数值来迫近系统的可靠性真值，这就是上下限法的基本思想。

上、下限法是首先求出系统的可靠度上限；然后假设并联单元不起冗余作用，全部作为串联处理求出系统可靠度的下限值；最后综合后得出系统的可靠度。上、下限法要分三个步骤进行：计算上限值、计算下限值及上下限的综合。

第一步：上限值的计算。当系统中并联子系统的可靠性很高时，可认为这些并联部件或冗余部分可靠度近似为1，系统失效主要是由串联单元引起的。

系统可靠度的上限初始值：

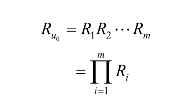
式中，Ri为系统中各串联单元的可靠度。

第二步：下限值的计算。把系统中所有组成单元都看成是串联的，得出系统可靠度的初始值。

系统可靠度的下限初始值：

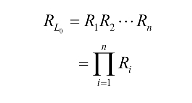
式中，Ri为系统中所有单元的可靠度。

考虑系统并联子系统中1个单元失效，系统正常工作的概率：

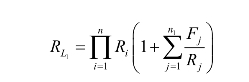
式中，n1为系统中并联单元数。

考虑的情况越多，结果越精确，计算也就越复杂，也就失去了这个方法的优点。

第三步：上下限的综合。按上下限值综合预计系统的可靠度：

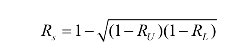
式中　Rs——系统中所有单元的可靠度；

RL——系统中所有单元的可靠度下限值；

RU——系统中所有单元的可靠度上限值。

【例5.1】　系统可靠性逻辑框图如图5.1所示，已知各单元的任务失效概率为

试用上、下限法求系统的可靠度，并与数学模型法的结果比较。

(www.xing528.com)

图5.1　某系统可靠性逻辑图

解（1）各单元的可靠度：

（2）系统的上限值：

（3）系统的下限值：

（4）系统的可靠度：

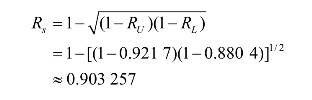
3.元件计数法（Element Counting Method）

元器件计数法是根据系统内包含的元器件数量及其可靠性水平来预计系统可靠度或MTBF的一种方法。该方法适用于方案阶段用以初步、快速估计设备可靠性水平。若一个系统的单元、器件的种类数为N，第i种元器件数量为ni，则系统的失效率为

4.相似产品法（Similar Product Method）

相似产品法是利用成熟的相似产品所得到的经验数据来估计新产品的可靠性。陈述产品的可靠性数据来自现场使用评价和实验室结果。这种方法在研制初期被广泛应用，也适用于研制的任何阶段。尤其是非典产品，查不到故障率数据，全靠自身数据的积累。成熟产品的详细故障记录越全面，比较的基础越好，预计的准确度就越高，当然还取决于产品的相似程度。

预计的基本公式：

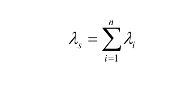
或者

式中　TBF——系统的MTBF（h）；

TBFi——第i个分系统的MTBF（h）。

5.故障率预计法（Failure Rate Prediction Method）

当研制工作进展到详细设计阶段，已有了产品原理图和结构图，选出了元部件，已知它们的类型、数量、环境及使用应力，并已具有实验室常温条件测得的故障率时，可采用故障率预计法。这种方法对电子与非电子产品均适用。其详细步骤为：

（1）根据产品功能图画出可靠性框图。

（2）按照可靠性框图建立相应的数学模型。

（3）确定各方框中元部件或设备的故障率，该故障率应为工作故障率，在实验室常温条件下测得的故障率为基本故障率。对于非电子产品，只考虑降额因子D和环境因子K对λ的影响。非电子产品的工作故障率为G

λ＝λG∙K∙D

式中　λ——工作故障率（1/h）；

λG——基本故障率（1/h）；

K和D的值根据工程经验确定。

6.专家评分法（Experts Grading Method）。

专家评分法需要依靠有经验的工程技术人员的工程经验，按评分结果，由已知的某单元故障率根据评分系数算出其余单元的故障率。

（1）评分考虑的因素可按产品特点而定。常用的有4种评分因素，每种因素的分数在1～10之间。以此类推。

①复杂度：根据分系统的元部件数量以及它们组装的难易程度来评定，最容易的评1分，最复杂的评10分。以此类推。

②技术发展水平：根据分系统目前的技术水平和成熟来评定，水平最低的评10分，水平最高的评1分。以此类推。

③工作时间：根据分系统工作时间来评定。系统工作时，分系统一直工作的评10分，工作时间最短的评1分。以此类推。

④环境条件：根据分系统所处的环境来评定，分系统工作过程中会经受极其恶劣和严酷的环境条件的评10分，环境条件最好的评1分。以此类推。

（2）专家评分的实施概要。已知某分系统的故障率为λn，计算出其他分系统故障率λi为

式中　i——分系统数量；

Ci——第i个分系统评分系数，且。

其中ω*是故障率为λ*的分系统的评分数；

ωi为第i个分系统的评分数，且

式（5.2）中，rij为第i个分系统、第j个因素的评分数，且j因素可以用数字表示，即j＝1表示复杂度、j＝2表示技术发展水平、j＝3表示工作环境、j＝4表示环境条件。