串联可修复系统的系统可靠性与安全性

串联可修复系统指的由n个单元与一组维修人员组成的串联系统。若n个单元都正常工作时，系统处于工作状态，当某个单元故障时，系统就出现故障。

1.n个相同单元情况

该串联系统在t与t+Δt之间极小时间内，若n个单元的故障率均为λ，修复率均为μ时，该系统状态转移如图3.20所示。

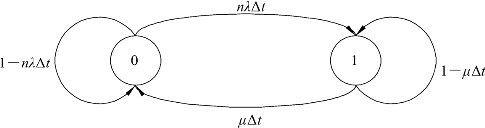
图3.20　n个相同单元串联状态转移图

其中　0——正常工作状态；

1——故障状态。

系统的微系数矩阵：

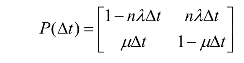
系统的状态转移形式与单元的可修复系统情况一致，只是n个单元以nλΔt的概率由正常状态向故障状态转移。则有

n个相同单元的有效度：

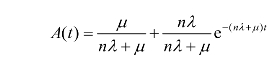
n个相同单元的稳态有效度：

在吸收状态时，系统可靠度：

R(t)＝e-nλt

在吸收状态时，系统首次故障前平均工作时间（MTTF）：

2.n个不同单元情况

该系统n个单元故障率并不相同，分别为λi，i＝1，2，…，n ；修复率分别为μi，i＝1，2，…，n ，其状态转移图如图3.21所示。(www.xing528.com)

图3.21　n个不同单元串联状态转移图

图3.21中的1指的是时刻t时第1个单元故障，其余单元都正常；以此类推，n表示时刻t时第n个单元故障，其余单元都正常。因此，该串联系统在t与t+Δt之间极小时间内的微系数矩阵为

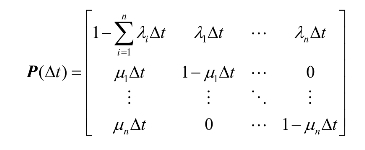
按照齐次马尔可夫可维修系统可靠性特征量的求解过程，写出相应P（Δt）所对应的P：

转移概率矩阵：

利用拉普拉斯变化，可以求出系统的稳态有效度：

其中，表示系统中第i个单元的维修系数。

由于系统的维修系数，则

由于系统的故障率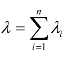，因此系统的平均修复时间为

若系统的可靠度仍为状态i处于吸收状态时的可靠度，则整个系统的可靠度：

系统首次故障前平均工作时间：