计算可修复系统的可靠性-随机过程与马尔科夫过程

为了计算可修复系统的可靠性，本章主要介绍随机过程理论、马尔科夫过程等经典数学理论。

1.随机过程理论（Random Process Theory）

随机过程是依赖于参数的一族随机变量的全体，参数通常是时间。随机变量是随机现象的数量表现，其取值随着偶然因素的影响而改变。目前，在自动控制、公用事业、管理科学等方面都有广泛的应用。

假设E是随机实验，e是随机试验的结果，S＝{e}是它的样本空间，T是一个参数集，若对于每一个t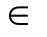T，都有随机变量X（e，t）与之对应，则称随机变量簇{x（e，t），t 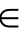T}为随机过程或随机函数，通常记作X（t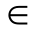），tT。

随机过程可以按照其状态进行分类：如果随机过程X（t）对于任意的t1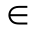T，X（t1）都是连续性随机变量，则称此随机过程为连续性随机过程；如果随机过程X（t）对于任意的t1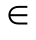T，X（t1）都是离散型随机变量，则称此随机过程为离散型随机过程。此外，随机过程还可以按照时间参数是连续还是离散进行分类。如果随机过程的参数变化范围T是有限或无限区间，X（t）叫作连续参数随机过程；如果T是可列个数的集合，如T＝{Δt，2Δt，…，n Δt，…}，X（t）则叫作离散参数随机过程或随机变量序列。

2.马尔可夫过程理论（Markov Process Theory）(www.xing528.com)

马尔可夫过程是一类随机过程。它的原始模型马尔可夫链，由俄国数学家A.A.马尔可夫于1907年提出。马尔可夫过程是研究离散事件动态系统状态空间的重要方法，它的数学基础是随机过程理论。

设{X（t），t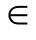T}的状态空间为S，如果，，在条件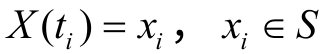，i＝1，2，…，n-1下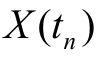，的条件分布函数恰好等于在条件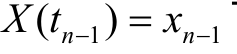下的条件分布函数，即

在马尔可夫过程中，tn时随机变量的概率与tn-1时随机变量的取值有关，而与tn-1以前的过程无关，这种性质称为“无记忆性”或“无后效性”。

由于马尔可夫过程是一个状态转移到另一个状态的过程，也是一种随机过程，因此可以按照时间和状态是离散还是连续进行分类，即：时间与状态均为离散的马尔可夫过程，称为时间离散马尔可夫链；时间连续、状态离散的马尔可夫过程，称为时间连续马尔可夫链；时间与状态均为连续的马尔可夫过程，称为连续马尔可夫链。