并联系统：二单元的平均寿命计算方法

并联系统是最简单的冗余系统（有贮备模型）。当所有单元都失效时，系统才丧失其规定功能；或者只要有一个单元正常工作，系统就能完成其规定的功能，这种系统称为并联系统。

组成系统的所有单元都发生故障时系统才发生故障，这种系统称为并联系统（Parallel System）。并联系统的结构如图3.6所示。

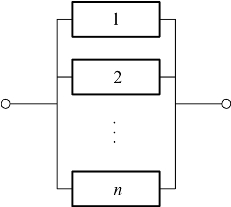
图3.6　并联系统的结构逻辑图

由n个独立的元件组成并联系统，有如下关系：

系统失效概率，即不可靠度为

由于元件是相互独立的，所以

式中　qi＝——元件失效概率。

假设单元的寿命为Xi，且，并联系统可靠度为

假定单元的寿命服从指数分布Ri（t）＝e-λit，则有

1.并联系统的属性特征

由n个单元组成的并联系统表示当这n个单元都失效时，系统才失效，换句话说，当系统的任一单元正常工作时，系统正常工作。

并联系统的不可靠度（累积失效概率）：

并联系统的可靠度：

2.并联系统的数学模型

即使单元故障率都是常数，但并联系统的故障率不再是常数，而是随着时间的增加而增大，且趋向于λ。由n个独立的元件组成并联系统，则系统可靠度：

（1）当系统各单元的寿命分布为指数分布时，对于n个相同单元的并联系统，则有

并联系统的可靠度：

Rs(t)＝1-(1-e-λt)n(www.xing528.com)

并联系统的平均寿命：

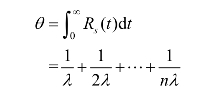
（2）当系统各单元的寿命分布为指数分布时，对于最常用的两单元并联系统，则有

并联系统的可靠度：

并联系统的失效率：

并联系统的平均寿命：

3.并联系统的主要特征

与无贮备的单个单元相比，并联可明显提高系统可靠性（特别是n＝2时）。当并联过多时，可靠性增速减慢，并联系统可靠度关系如图3.7所示。

根据图3.7，可知并联系统的主要特征如下：首先，并联系统的失效概率低于各单元的失效概率；其次，并联系统的平均寿命高于各单元的平均寿命；并联系统的可靠度大于单元可靠度的最大值；再次，并联系统的各单元服从指数分布，该系统不再服从指数分布；最后，随着单元数的增加，系统的可靠度增大，系统的平均寿命也随之增加，但随着数目的增加，新增加单元对系统可靠性及寿命提高的贡献变得越来越小。

图3.7　并联系统可靠度关系

【例3.2】设某种单元的可度为　R0（t）＝e-λt，其中λ＝0.002，试求出：

（1）由这种单元组成的二单元并联系统的平均寿命。

（2）当t＝200 h，400 h，600 h，800 h 时，二单元并联系统的可靠度。

解　（1）系统的平均寿命为

（2）当t=200 h 时，系统的可靠度为

当t=400 h ，系统的可靠度为

当t＝600 h ，系统的可靠度为

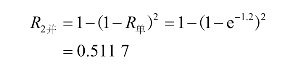
当t=800 h ，系统的可靠度为