【摘要】：二项分布函数又称伯努利分布函数。，n，共1n+种，这时X服从的概率分布称为二项分布。假设二项分布满足：试验次数n是一定的；每次实验结果只有成功或者失败，成功概率为p，失败概率为q，满足p+q＝1；所有实验都是相互独立的，则二项分布的特征向量函数为二项分布的数学期望：E＝np二项分布的方差：D＝σ2＝npq＝np(1-p)二项分布的可靠度：二项分布函数的用途很广泛，如在可靠性设计中，可用来解决冗余部件的可靠度分配问题。
二项分布（Binomial Distribution）就是重复n次独立的伯努利试验。每次试验只有两种可能的结果，而且两种结果发生与否互相对立，并且相互独立，与其他各次试验结果无关，事件发生与否的概率在每一次独立试验中都保持不变。二项分布函数（Binomial Distribution Function）适用于一次试验中只能出现两种结果的场合，如成功与失败、命中与未命中、次品与合格品等，这两种结果的事件分别用A与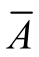
表示，设它们发生的概率分别为P（A）＝P，
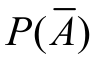＝1-P，现在独立地重复做n次试验，那么在n次试验中事件A恰好发生k次的概率是多少？
二项分布函数（X～B（n，p））又称伯努利分布函数（Binomial Distribution Function）。以X表示在n重独立试验中事件A发生的次数，则X是一个随机变量，它的可能取值为0，1，…，k，…，n，共 1n+种，这时X服从的概率分布称为二项分布。假设二项分布满足：
（1）试验次数n是一定的；
（2）每次实验结果只有成功或者失败，成功概率为p，失败概率为q，满足p+q＝1；
（3）所有实验都是相互独立的，
则二项分布的特征向量函数为
二项分布的数学期望（Expectation）：(www.xing528.com)
E(X)＝np
二项分布的方差（Variance）：
D(X)＝σ2＝npq＝np(1-p)
二项分布的可靠度（Reliability）：
二项分布函数的用途很广泛，如在可靠性设计中，可用来解决冗余部件的可靠度分配问题。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
