故障率函数：系统可靠性与安全性简介

故障率函数（Failure Rate Function），也叫失效率函数。工作到某时刻尚未发生故障的产品或系统，在该时刻之后单位时间内发生故障的概率，称之为故障率。

失效率（瞬时失效率）（Failure）指工作到t时刻尚未失效的产品，在该时刻t后的单位时间内发生失效的概率，也称为失效率函数，记为　λ（t）。失效率用数学符号表示为

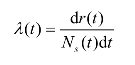
式中　λ(t)——失效率；

d(r)t——t时刻后，dt时间内故障的数量；

Ns(t)——残存数量，即到t时刻尚未发生故障的数量。

1.失效率的简化算法

由失效率的定义可知，在t时刻完好的产品，在（t，t+Δt）时间内失效的概率为： P（t﹤T≤t+Δt|T﹥t）。失效率可做如下计算：

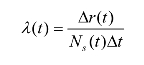
式中　Δr(t)——t时刻后，Δt时间内故障的产品数；

Δt——所取时间间隔；

Ns(t)——残存产品数。

2.累积失效概率（不可靠度）与失效概率密度的关系

累积失效概率（不可靠度）与失效概率密度之间有着密切关系，是一种函数关系。因此，失效率表示为

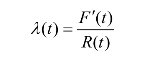
则累积失效概率（不可靠度）与失效概率密度的关系为

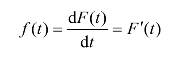
3.失效率的单位(www.xing528.com)

失效率λ（t）是一个非常重要的特征量，它的单位通常用时间的倒数表示。但对目前具有高可靠性的产品来说，就需要采用更小的单位作为失效率的基本单位，因此失效率的基本单位用菲特（Fit）来定义。

注：①1 菲特＝10-9/h＝10-6/1000 h ；

②1 菲特的意义是每1 000 个产品工作106h，只有一个失效。

2.1.7　故障率与可靠度、故障密度函数的关系

故障率与可靠度、故障密度函数三者之间有一定的关系，这种关系可以用函数表达出来。由于故障率可表示为

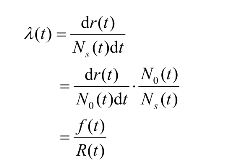
由密度函数的性质可知，故障率与可靠度、故障密度函数有如下关系：

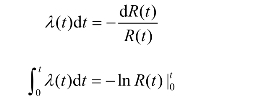
其中

可靠度函数

注意：

R(0)＝1，R(∞)＝0

F(0)＝0，F(∞)＝1

R（t），F（t）与f（t）等之间的函数关系如图2.2 所示。

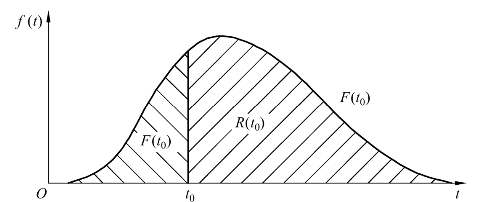
图2.2　R（t），F（t）与f（t）的关系