【摘要】:可靠度是可靠性的度量,一般指的是产品在规定的条件下和规定的时间内,完成规定功能的概率。依定义可知,系统的可靠度是时间的函数:R=P(ξ﹥t)式中R——可靠度函数;ξ——产品正常工作时间;t——规定的时间。产品的寿命ξ大于t。由可靠度的定义可知,R描述了产品在(0,t)时间段内完好的概率,且0≤R≤1,R=R(+∞)=0上述公式表明,开始使用时,所有的产品都是良好的,只要时间充分长,全部的产品都会失效。
可靠度(Reliability)是可靠性的度量,一般指的是产品在规定的条件下和规定的时间内,完成规定功能的概率。依定义可知,系统的可靠度是时间的函数:
R(t)=P(ξ﹥t)
式中 R(t)——可靠度函数;
ξ——产品正常工作时间;
t——规定的时间。
事件(ξ﹥t)有三个含义:
(1)产品在t时间内完成规定的功能。
(2)产品在t时间内无障碍。
(3)产品的寿命ξ大于t。
显然,规定的时间t越短,系统完成规定功能可能性越大;规定的时间t越长,系统完成规定功能的可能性就越小。(https://www.xing528.com)
由可靠度的定义可知,R(t)描述了产品在(0,t)时间段内完好的概率,且
0≤R(t)≤1,R(0)=R(+∞)=0
上述公式表明,开始使用时,所有的产品都是良好的,只要时间充分长,全部的产品都会失效。
如前所述,这个概率是真值,实际上是未知的。在实际应用中常用它的估值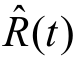 。
。
假如在t=0时有N0件产品开始工作,而到t时刻,有r(t)个产品失效,仍有N0-r(t) 个产品继续工作,则可靠度R(t)的估计值:
式中:N0——当0t=时,在规定条件下进行工作的产品数;
r(t)——在0到t时刻工作时间内产品的累计故障数。
由可靠度的定义可知,R(t)描述了产品在(0,)t时间内完好的概率,且R(0)=1,R(∞)=0。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




