(一)点缓冲区的建立
点缓冲区的建立从原理上来说相当地简单,即建立以点状要素为圆心、半径为缓冲区距离的圆周所包围的区域,其算法的关键是确定点状要素为中心的圆周。若要将多个点缓冲区合并,则可采用圆弧弥合的方法:将圆心角等分,用等长的弧代替圆弧,即用均与步长的直线段逼近圆弧。
(二)线缓冲区的建立
线缓冲区的建立比较复杂:先生成缓冲区边界,然后对可能出现的尖角和凹陷等特殊情况做进一步的处理,最后进行自相交处理以区别缓冲区的外边界和岛边界。缓冲区计算的基本问题是双线问题,主要有角平分线法和凸角圆弧法。
1.角平分线法
角平分线法的基本思想是:在轴线首尾处作轴线的垂线,按缓冲区半径R截出左右边线的起止点并对轴线作其平行线;在轴线的其他转折点上,用与该线所关联的两邻线段的平行线的交点来生成缓冲区对应顶点,见图4-5。
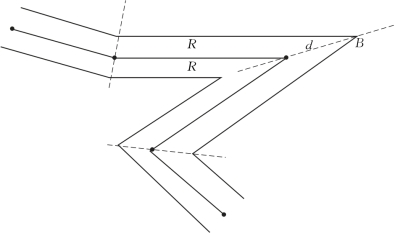
图4-5 角平分线法(https://www.xing528.com)
角分线法的缺点是难以最大限度保证双线的等宽性,尤其是在凸侧角点在进一步变锐时,将远离轴线顶点。当缓冲区半径不变时,d随张角B的减小而增大,结果在尖角处双线之间的宽度遭到破坏。因此,为克服角分线法的缺点,要有相应的补充判别方案,用于校正所出现的异常情况。但由于异常情况不胜枚举,导致校正措施复杂。
2.凸角圆弧法
在轴线首尾点处,做轴线的垂线并按双线和缓冲区半径截出左右边线起止点;在轴线其他转折点处,首先判断该点的凸凹性,在凸侧用圆弧弥合,在凹侧则用前后两邻边平行线的交点生成对应顶点。这样外角以圆弧连接,内角直接连接,线段端点以半圆封闭,见图4-6。
在凹侧平行边线相交在角分线上。交点距对应顶点的距离与角分线法类似公式见式(4-4)。
![]()
该方法最大限度地保证了平行曲线的等宽性,避免了角分线法的众多异常情况。

图4-6 凸角圆弧法
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




