车联网系统：基于Petri网模型的物流配送性能分析

利用Petri网建立配送业务流程模型，可以将业务流程很直观地展现，对模型进行性能分析，能够对模型的正确性进行检验，及时解决模型中存在的问题，保证了模型的可用性。

（1）利用Petri网理论进行性能分析

通过Petri网的S（库所）-不变量和T（变迁）-不变量的分析方法对模型的基本性质（可达性、有界性、活性等）进行分析以验证模型的正确性、可用性。

S-不变量和T-不变量是一对对偶量，是在关联矩阵A的基础上，利用数学代数原理对Petri网进行分析的一种方法。

若存在m维非负整数向量Y满足AY=0，则称Y为网N的S-不变量。

若存在n维非负整数向量X满足A^TX=0，那么X为网N的T-不变量。

Petri网模型的输出矩阵A⁺如下所示：

Petri网模型的输入矩阵A-如下所示：

由关联矩阵A=A+-A-可以得出，关联矩阵A如下所示：

T-不变量表示变迁按照一定的顺序发生后仍能回到原点，表示的是一种循环结构，观察物流配送Petri网模型可知其变迁T-不变量为0。因此在计算Petri网不变量时可以省去变迁T-不变量的计算，直接计算S-不变量。

由AY=0，其中向量Y为非平凡的m维非负整数向量，可以得出网N的S-不变量Y为

(www.xing528.com)

对应的模型潜在路径为

分析以上三条路径可知，该物流配送模式的Petri网模型中的每一个库所都是可达的并且每一个变迁都是可以触发的，因此可以判断该改进Petri网模型是可达的、活的、不存在死锁和冲突的情况。在该模型中每个库所中的最大资源数均为1，由Petri网的有界性和安全性定义可以判断该Petri网模型是有界的、安全的。综上所述，可以说明物流配送的Petri网模型是正确的、可用的。

（2）运用Petri网软件进行性能分析

运用Petri网软件P.I.P.E.（Platform Independent Petri Net Editor）对图6-14的基于车联网的物流配送模式的Petri网模型进行建模分析，如图6-18所示。

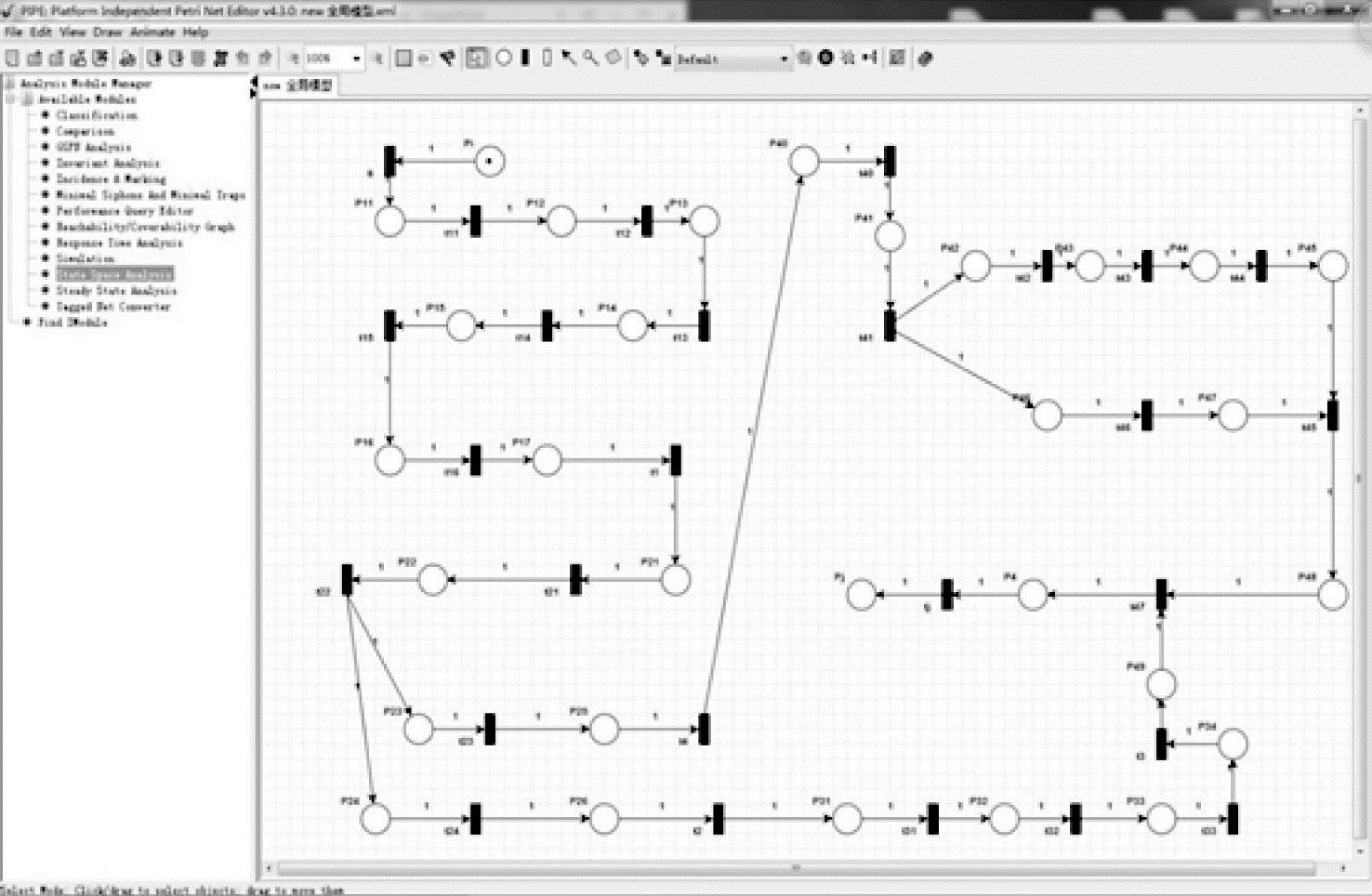
图6-18　基于车联网的物流配送模式的P.I.P.E.软件模型

通过双击图6-18中界面左侧的State Space Analysis，对基于车联网的物流配送模式的Petri网模型进行稳定性检测，检测结果如图6-19所示。

如图6-19所示，其中Bounded的属性值为TRUE，表示该Petri网模型是有界的；Safe的属性值为TRUE，表示该Petri网模型是安全的；Deadlock的属性值为TRUE，表示该Petri网模型不存在死锁，即该Petri网是活的。

由图6-19的稳定性分析结果可以看出，图6-14所示的基于车联网的物流配送模式的Petri网模型是活的、有界的和安全的。

综上所述，无论从数学解析角度，即关联矩阵的角度分析，还是利用Petri网软件工具分析，得出的结论是一致的，即图6-14中基于车联网的物流配送模式的Petri网模型是正确的、可行的。

图6-19 基于车联网的物流配送模式的Petri网模型的稳定性检测结果