车联网系统：模型性能分析成果

利用Petri网来对企业业务流程进行建模，主要目的之一是借助系统Petri网模型分析企业业务流程的性质和功能。如果一个Petri网模型确切地描述了一个业务流程的结构和运行，那么这个业务流程所具有的一些性质也会在Petri网模型上得到体现。这些性质与Petri网所模拟的业务流程运行过程中的某些方面的性质有密切联系，因此，Petri网模型建立完毕后需要对模型进行性质分析。Petri网模型的性质的分析主要有可达性、有界性、活性等。

1.模型的可达性

可达性是Petri网的最基本的动态性质，其余各种性质都要通过可达性来定义。Petri网的结构可以用一个矩阵来表示。设Σ=（S，T；F，M）为一个Petri网，S={s₁，s₂，…，s_m}，T={t₁，t₂，…，t_n}，则Petri网Σ的结构（S，T；F）可以用一个n行m列矩阵

A=[a_ij]_n×m （6-1）

来表示，其中

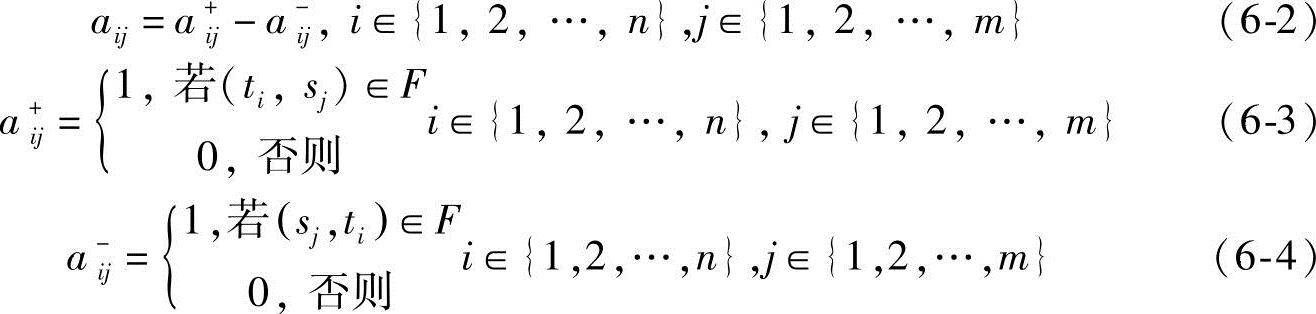
称A为Σ（或网N=（S，T；F））的关联矩阵（incidencematrix）。

为方便讨论，引入两个n行m列矩阵

A⁺=[a+ij]_n×m （6-5）

A^-=[a-ij]_n×m （6-6）

分别称为Σ（或网N=（S，T；F））的输出矩阵和输入矩阵。

对于无循环回路的Petri网，状态方程存在非负整数是标识M可达的充分必要条件，这就简化了可达性的判断问题。M₀为其初始标识，若M∈R（M₀），则存在非负整数的n维矢量X，使得

M=M₀+A^TX （6-7）

2.模型的有界性

设Σ=（S，T；F，M）为一个Petri网，s∈S。若存在正整数B，使得∀M∈R（M₀）∶M（s）≤B，则称库所s为有界的（bounded），并称满足此条件的最小正整数B为库所s的界，记为B（s）。Petri网的有界性（boundedness）反映被模拟系统运行过程中对有关资源的容量要求。虽然作为Petri网，从定义上对每个库所的容量不加限制，但如果对某个库所s，求出B（s）=k，那么在系统设计时，只要库所s所表示的资源的容量不小于k，就能保证系统的正常运行。

3.模型的死锁性

死锁是网中一种特殊的库所子集。设N=（S，T；F）为一个网，S₁⊆S。如果·S₁⊆S₁·，则称S₁为网N的一个死锁。

如图6-15中的网N₁中，{s₁，s₂}是一个死锁，由于

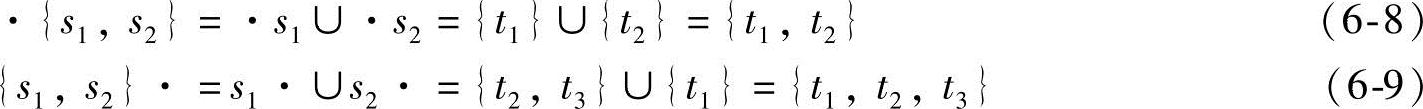(www.xing528.com)

即满足·{s₁，s₂}⊆{s₁，s₂}·，所以{s₁，s₂}是网N₁的一个死锁。

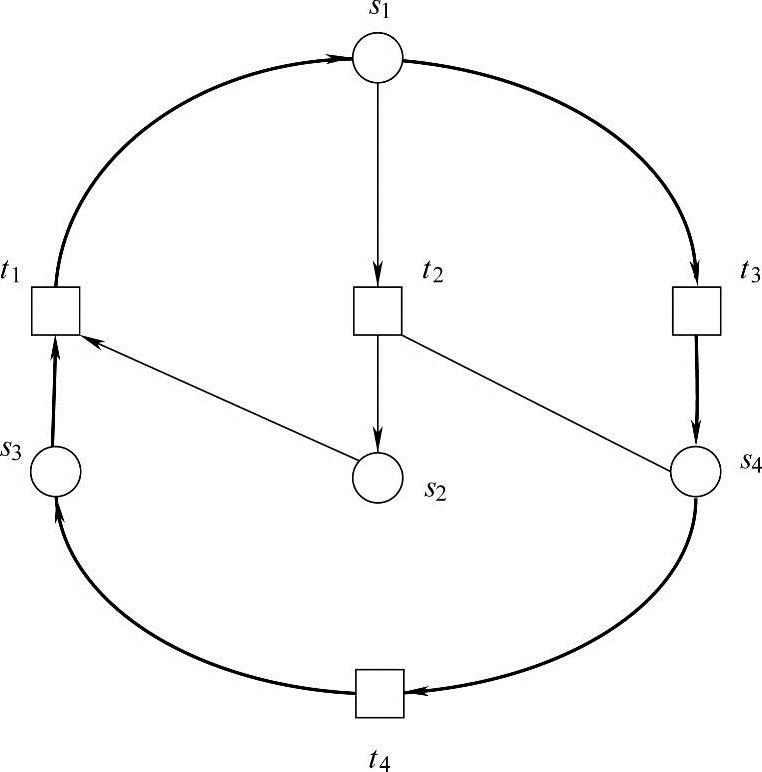
图6-15 网N1

4.模型的活性

设Σ=（S，T；F，M₀）为一个Petri网，M₀为初始标识，t∈T。如果对任意M∈R（M₀），都存在M′∈R（M），使得M′[t＞，则称变迁t为活的。如果每个t∈T都是活的，则称Σ为活的Petri网。

如图6-16所示的Petri网网N₂，在这个网系统中，变迁t₁和t₂是活的，但变迁t₃不是活的（事实上，在任何可达标识下t₃都不可能发生）。从而这个网系统不是活的。

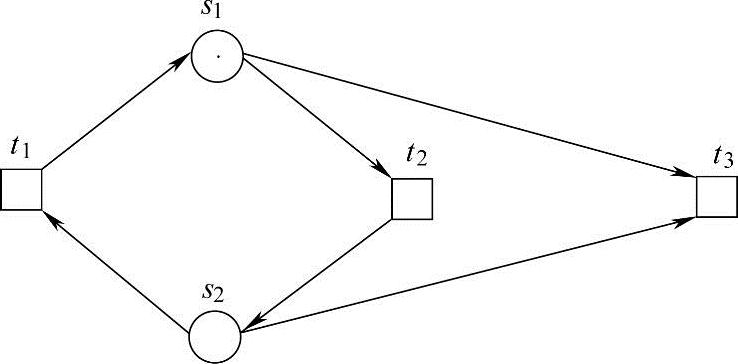
图6-16 网N2

5.模型的冲突性

在Petri网中，在某一个标识下，多个变迁都可能发生，其中一个变迁的触发导致其他变迁失去了发生权，这种情况称为冲突。冲突关系描述了系统的非确定性：在某情况下有两个（或多个）事件都有权发生，但在实际运行过程中，只有一个能真正发生，系统存在冲突之处，正是外界环境可以对其施加控制（加以选择）。

如图6-17所示，图中网N₃变迁t₁与t₂触发均需库所s₁中的资源，若变迁t₁得到s₁中的资源发生，则变迁t₂失去了发生权，这就是冲突。

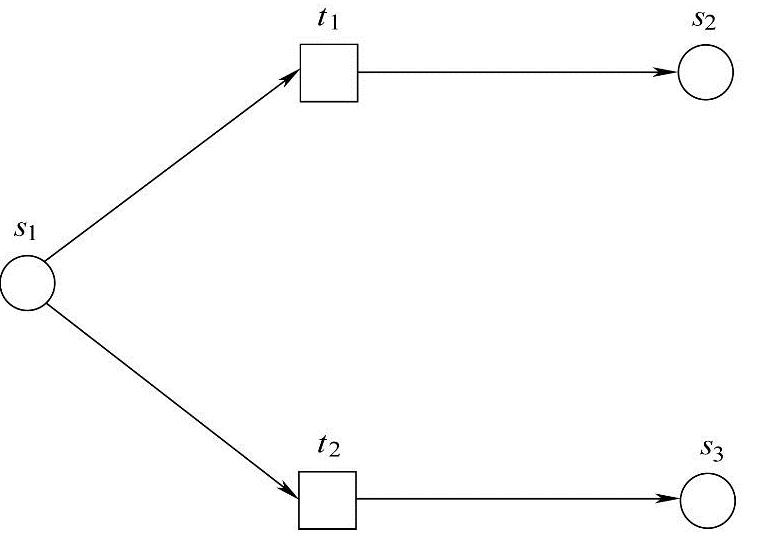
图6-17 网N3

6.S-不变量与T-不变量

S-不变量和T-不变量是一对对偶量，它是在关联矩阵的基础上，利用数学代数原理对Petri网进行分析一种方法。

设N=（S，T；F）是一个Petri网，丨S丨=m，丨T丨=n，A为N的关联矩阵。

1）若存在非平凡的m维非负整数向量Y满足AY=0，则称Y为网N的S-不变量。S-不变量中各分量的值表示对应库所的加权值，与对应库所中的托肯数相乘后得到的值在系统中保持不变，体现了Petri网系统库所中托肯数的加权守恒性，可以用来对网系统进行互斥、死锁等检测。

2）若存在非平凡的n维非负整数向量X满足A^TX=0，那么X为网N的T-不变量。T-不变量表示与之相对应的网系统中的变迁发生后可以恢复到初始时的标识状态，即网系统经过多次运行后仍能回到原点，体现了网系统的可复制性和活性，可用于分析网系统的周期性等性能。