基于路段划分的路段旅行时间估计方法

动态路径诱导系统（DRGS）需要提供基于实时交通信息的动态路径规划，而路网的动态属性对于路径选择尤为重要，因此，对于动态路径诱导而言，关键问题是建立随时间变化的动态路网图。这里假设路网图记为（V，E），其中，V代表顶点集合，E代表边的集合。每一条边e∈E有如下属性：两个顶点e_v1和e_v2，以及权重e_cost。路网的拓扑结构可以通过电子地图来获取，因而最关键的问题是如何从实时交通数据中计算每个路段的权重。我们需要用一个参数来衡量路段的权重。Vuren和VanVliet^[6]认为距离最小和时间最小是驾驶人选择路径的仅有的两个参数。Bovy和Stern^[7]的进一步研究表明，除了时间和距离两个参数，还有更多的因素影响驾驶人的路径选择行为，如路段的宽度、路段的延时、路段的安全性、交通密度等。一般来讲，当前基于路径距离或者历史交通流信息的最短距离或者最少旅行时间的路径诱导系统中，旅行距离和旅行时间一般被认为是决定路径选择的主要因素，但是距离对于给定的路网和选定的路径是静态参数，因而不适合用于动态路网的路段权重衡量中。所以，本节采用旅行时间作为衡量路段权重的因素来构建动态路网图。

在路网图中，定义E为路段。一般都把路段定义为两个交通节点之间路段，这里交通节点指的是十字路口的中心或者两个相邻交叉路口停车线之间的路段。但是，传统的划分方法在利用浮动车估计平均旅行速度方面遇到了许多问题，因为在路段的不同部分交通状况随时间变化明显。而根据固定的路段划分方法估计，不能完全反映路段的交通状况，那么这将降低估计的旅行时间的精度，从而最终导致交通状态估计的不准确，造成路径选择的不合理。

因此，考虑到相邻车辆通常有着相同或者相似的交通状况，这里提出了通过对实时数据的分析的动态路段划分的概念。通过这个划分过程，一条路段可以划分成一个或者更多的子路段，每个子路段可以计算得到相应的旅行时间。这样，路径诱导问题最终变为路段的划分及子路段的旅行时间的计算问题。下面详细介绍我们提出的方法。

1.基于DBSCAN聚类的路段动态划分

由于路段上车辆的分布是不均匀的，路段上的不同区域有着不同的拥堵程度，所以，在路段的不同区域车辆聚集在一起，通过聚集的车辆可以把路段分成不同的子路段（图5-9）。因此，可以使用基于密度的聚类算法对路段的车辆的位置信息进行聚类处理，DBSCAN（Density-Based Spatial Clustering of Applications with Noise）^[8]是一个比较有代表性的基于密度的聚类算法，它将簇定义为密度相连的点的最大集合，能够把具有足够高密度的区域划分为簇，并可在噪声的空间数据库中发现任意形状的聚类。这样就可以很快地识别出路段上不同区域的密度，从而实现路段的动态划分，下面详细介绍路段划分的方法。

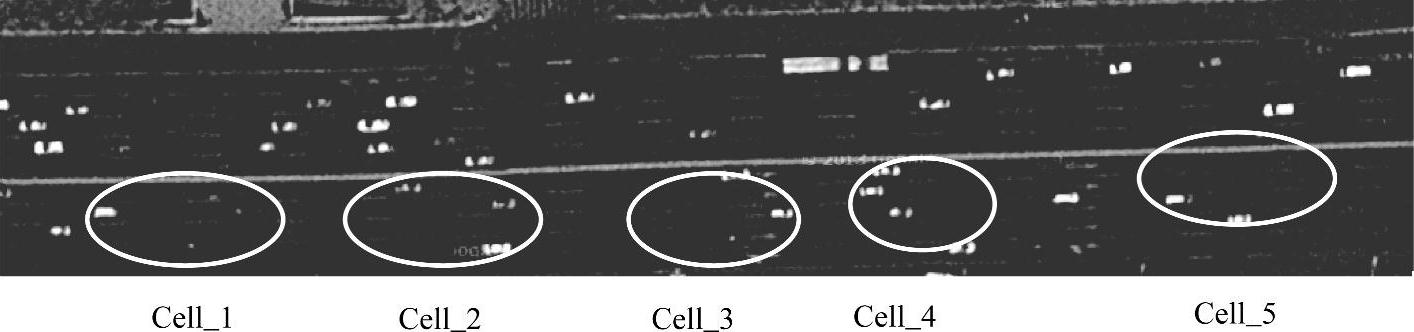
图5-9 谷歌地图显示车辆聚类现象

在指定时间内从路径诱导系统中采集的车辆实时状态信息根据GPSID顺序存储于数据库中。假设这些GPS数据已经匹配到电子地图上，并且根据相应的路段存储在数据库中。数据格式见表5-5。

表5-5 路段数据存储格式

表中，roadid表示路段编号。startpoint_lat、startpoint_lng、endpoint_lat、end-point_lng代表自然路段的两个节点地理信息。carid、lat、lng、speed、time代表车辆的实时位置信息，这些信息根据离路段某个节点的距离排列：其中，carid代表车辆的编号；lat、lng代表车辆的位置信息；speed代表数据传输时车辆的实时速度；time代表数据传输时的发送时间。

这样就得到记录路段交通信息的表格。因而，下面的工作是如何通过上述的实时信息来计算路段的旅行时间。描述子路段的属性的定义如下。

定义1（AdjacentVehicle）：根据车辆p和车辆q之间的距离（如欧氏距离），即dist（p，q），来判断两辆车是否是毗邻的。在仿真中，车辆位置可以定义为点（x，y）。因此，本书采用欧氏距离来计算车辆之间的距离。两点之间的欧氏距离定义为

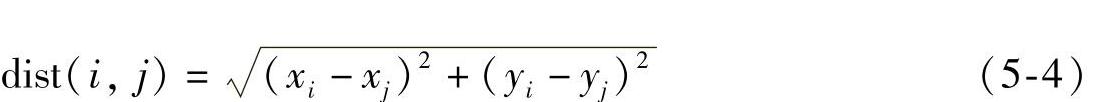
其中，i=（x_i，y_i）和j=（x_j，y_j）是两个位置数据点。

定义2（Eps-adjacentvehicles）：对于车辆p的Eps邻域内的车辆可以定义为{q∈D|dist（p，q）≤Eps}。

定义3（Corevehicle）：核心车辆指的是该车的Eps邻域内车辆的数目至少大于一个最小值（MinPts）。

定义4（Cellandnoise-vehicle）：在给定的一个数据集中，对某个核心车辆所有密度可达的车辆构成一个聚类。不包含于任何一个聚类的车辆，称为噪声车辆。

根据上述定义，我们能够判断数据点是否能够被合理聚类，聚类结构将能够合理地反映道路的上车辆分布的不均匀性，以及密度较大的车辆簇的位置。使用DBSCAN聚类算法划分路段实时信息的过程概括如图5-10所示。

图5-10 基于DBSCAN的路段划分算法

图5-10 基于DBSCAN的路段划分算法（续）

用图5-11作为实例来解释上述算法。由图中可以看到，路段包括两个节点，一个入口和一个出口。二者之间，有N辆车分布在其中。首先，Eps和MinPts这两个参数需要确定。Eps代表确定毗邻车辆的门限值，MinPts代表在核心车辆的邻域内毗邻车辆的最小数目。此算法从数据集LinkD中的第一点P₁（表示图中车辆A的位置）开始并遍历P₁的密度可达的所有点，这样就形成了在P₁领域内的局部密度，这里记为density（P₁）=Count（N_Eps（P₁））。

图5-11 算法实例(www.xing528.com)

其中，Count（N_Eps（P₁））代表P₁领域内车辆的总数，N_Eps（P₁）代表P₁领域内所有的车辆，即，N_Eps（P₁）={P_j∈LinkD|∀j，distance（P_j，P₁）＜Eps}。

在车辆A的领域内，有5辆车。这里设置MinPts为4，所以根据局部密度大于Minpts，车辆A被认为是核心车辆。这样一个聚类就形成了。通过上述步骤，三个聚类结果形成，同时有两个噪声点。从中可以看到，在噪声点处的路段车辆密度是稀疏的，所以噪声点不影响旅行时间估计。最终得到若干辆车组成的三个子路段。这里定义每个路段的聚类数为CNum。

2.路段旅行时间估计

这部分通过上面的聚类结果来进行路段旅行时间的计算，包括聚类数和路段的聚类内容。根据聚类数，可将路段分为两类来计算路段旅行时间。这两种路段定义如下：

1）类型1，如果路段的聚类数大于1，那么路段可划分成若干不同的子路段。

2）类型2，如果路段的聚类数为1或者为0，那么路段处于拥堵状况，高密度的车辆汇集成一个聚类，或者没有车辆经过该路段。

对于类型1，根据聚类数目，每个路段可以被划分成若干个子路段。假设第i个子路段的长度记为l_i，其值为该路段上距离自然路段两个自然节点距离最近的两车辆的间距；那么，子路段的平均速度可以通过式（5-5）得

式中，v_gⁱ为第i个子路段中第g个车辆的速度；D_i为第i个子路段中的车辆的总数。

那么，第i个子路段的旅行时间t_i可由式（5-6）获得

将各个自然路段中的相邻子路段内间距最小的两车辆间的路段作为未划分路段，则自然路段中的全部未划分路段的总通行时间t_others可以通过式（5-7）得

式中，l为自然路段的总长度；l_i为第i个子路段的长度；V_max为自然路段的设计速度，即车辆在该自然路段行驶的允许的最大速度；CNum为自然路段内子路段的数量。

由此可以得到路段的旅行时间为

若自然路段内第k个子路段中没有子聚类或仅有一个子聚类，即对于第二种类型的路段，由于路段并未通过提出的方法划分，所以就利用路段的自然属性来计算路段的旅行时间。事实上，这种路段可能很拥堵或者很通畅，所以没有必要划分，则此时自然路段的平均速度为

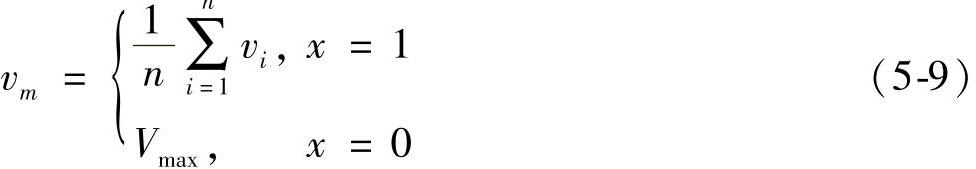
式中，v_i为自然路段中第i个车辆的速度；n为自然路段中车辆的总数；V_max为自然路段的设计速度，即车辆在该自然路段行驶的允许的最大速度。

从而，路段的旅行时间可以通过式（5-10）得

那么，每条路段的权重可以记为

最后，动态路网图可表示为连通网络图G（N，E，W），N为连通网络图中的自然节点数，N={1，2，3，…，h}；E为连通网络图中所有自然路段的集合，E={（r，s）∈N×N}；r、s分别为各个自然路段的两个端点；W={w_rs}为连同网络图中各个自然路段的权重集合。