车联网系统：交通应急疏散方法

面向车联网应用环境，本小节重点研究交通应急疏散优化方法并搭建了车联网交通应急疏散原型系统。由于车联网能够较好地为后台服务器和移动终端提供实时数据交互业务功能，以车联网提供的实时地理位置信息和无线数据传输保障了交通应急疏散的可靠性和高效性。通过在车联网环境下进行智能移动终端、地理位置服务功能和移动通信功能的深度融合，构建交通应急疏散优化方法框架，可为车联网在交通应急领域的应用提供重要的研究范例。

面向车联网应用环境的交通应急疏散方法架构，主要包括四大逻辑组件模块：一是基于图论邻接矩阵描述的实际交通路网拓扑表达模块；二是基于Dijk_- stra-Yen算法的交通应急疏散抽象拓扑图构建模块；三是基于整数规划模型的疏散交通流最优分配模块；四是基于车联网的疏散路径信息发布模块。具体的应急疏散优化方法架构如图4-3所示。

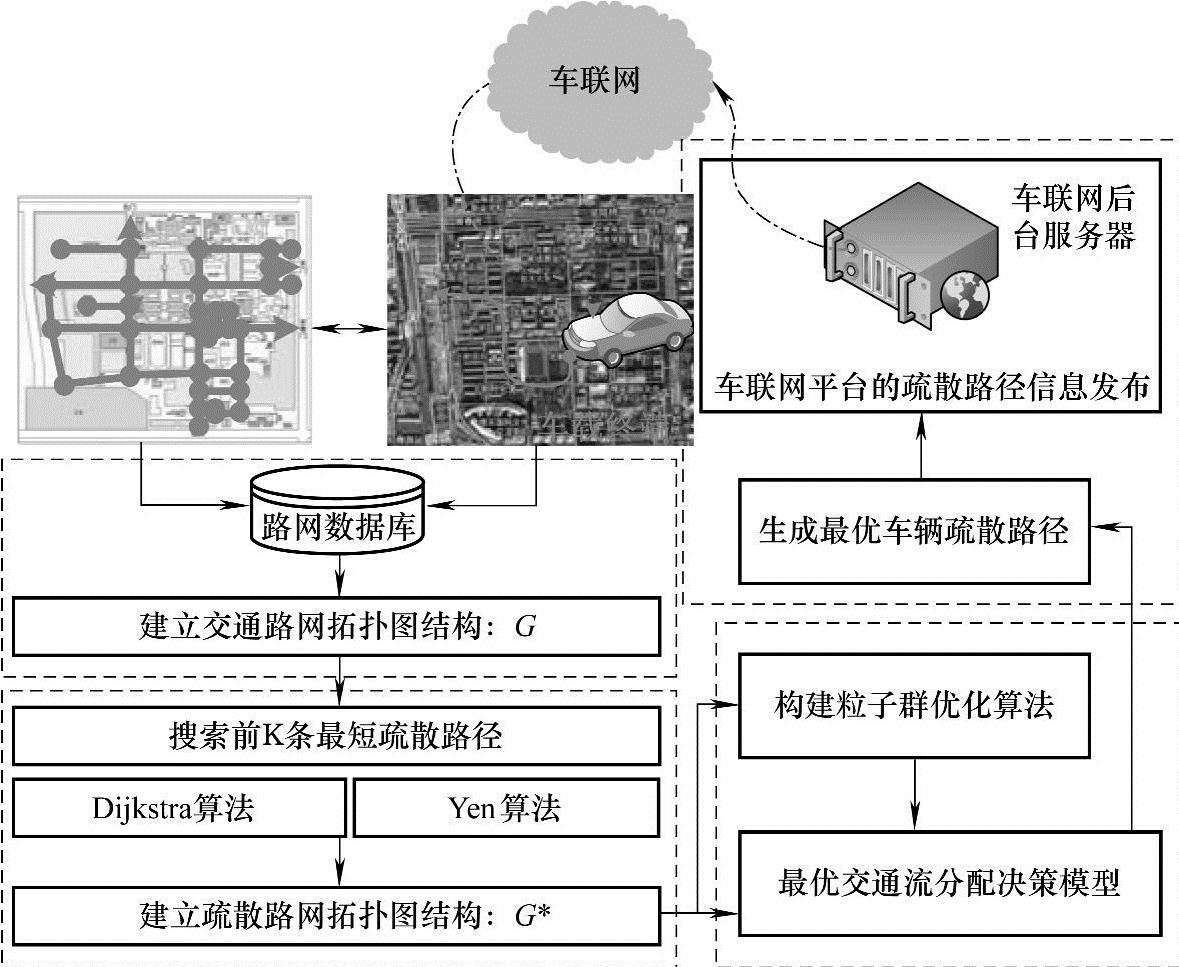
图4-3 面向车联网的交通应急疏散方法

（1）实际交通路网拓扑表达模块的设计与实现

采用图论的方法描述交通安全应急疏散的实际路网结构，记有向拓扑图为G=（V，E）；其中，V为表征实际路网中路段与路段之间交叉口的拓扑顶点集合，且有V={v₁，v₂，…，v_n}，v_i（i=1，2，…，n）表示第i个拓扑顶点；E为表征实际路网中路段的拓扑边集合，且有E={e₁，e₂，…，e_m}，e_j=（v_k，v_l）表示从顶点vk到顶点v_l连接的有向弧，即第j个拓扑边。为了进一步利用车联网后台服务器道路信息数据库提供的实时交通信息，采用邻接矩阵A=A（G）=[a_ij]_n×n刻画拓扑图G中顶点与顶点之间的邻接关系以表征实际路网中路段的连通性，其中a_ij表示顶点v_i与顶点v_j之间的边数，可能取值为0、1、2等。在具体实现过程，采用稀疏矩阵数据结构代替拓扑图的邻接矩阵数据结构，并存储于网络后台数据库中。

网络后台数据库可通过车联网采集得到车载终端发送的地理位置信息和车速数据，记无线传输的数据格式为[p（i）.longitude（t），p（i）.latitude（t），p（i）.velocity（t）]，其中p（i）.longitude（t）和p（i）.latitude（t）表示第i个车辆终端p（i）在第t时刻传回的经纬度数据，该时刻传回的车速数据用p（i）.velocity（t）表示。采用拓扑边的长度，记为e_k.length且e_k=（v_i，v_j），以及该路段上车辆通过车联网传回网络后台数据库的实时地理位置信息及车速计算获得拓扑边的权重量化值：

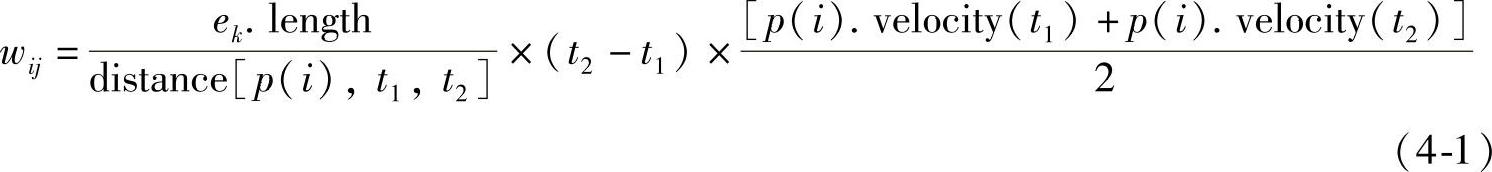
式中，当a_ij=0时表示顶点v_i与顶点v_j不连通，则e_k.length=+∞，否则当a_ij≥1时e_k.length取为拓扑边e_k所表征的实际路段长度；t₁和t₂为连续两个采样时刻，且满足t₁＜t₂；参数distance[p（i），t₁，t₂]表示利用该路段上车辆p（i）在t₁和t₂传回的经纬度数据计算得到的p（i）在这两个时刻位置距离值[13]；参数w_ij即表示拓扑图边e_k=（v_i，v_j）的权重量化值。

邻接矩阵A=A（G）=[a_ij]_n×n和权重矩阵W=W（G）=[w_ij]_n×n分别刻画了路网的拓扑结构特征和路段车辆行驶阻抗特征，作为下一模块的输入信息，为Di-jkstra-Yen算法提供计算基础。

（2）交通应急疏散抽象拓扑图构建模块的设计与实现

在实际路网结构信息基础上，需要为应急交通流进一步确定安全疏散的路径集合。如果将源点上的疏散交通流直接分配到整个路网上，则为了计算得到最优的疏散交通流分配策略，需要对整个路网结构进行最优搜索程序，由于计算复杂性和计算耗时巨大，所述搜索程序在面向实际大规模路网结构的应用中将无法实施。因此，考虑每一个交通疏散源点到每一个疏散目的地前k条最短路构成的集合G^*，该集合是整个路网G的子集，以此集合G^*作为交通应急疏散的抽象拓扑路网实施交通流分配可有效地降低计算复杂性和计算耗时。图4-4给出一个示例：假设疏散交通流源点分别为S1、S2和S3，疏散目的地为d1，则基于实际路网拓扑结构G的A=A（G）=[a_ij]_n×n和W=W（G）=[w_ij]_n×n，计算获得交通流从S1、S2和S3疏散至d1的路径集合G^*，该路径集合构成G的子集，可作为交通应急疏散抽象拓扑路网。

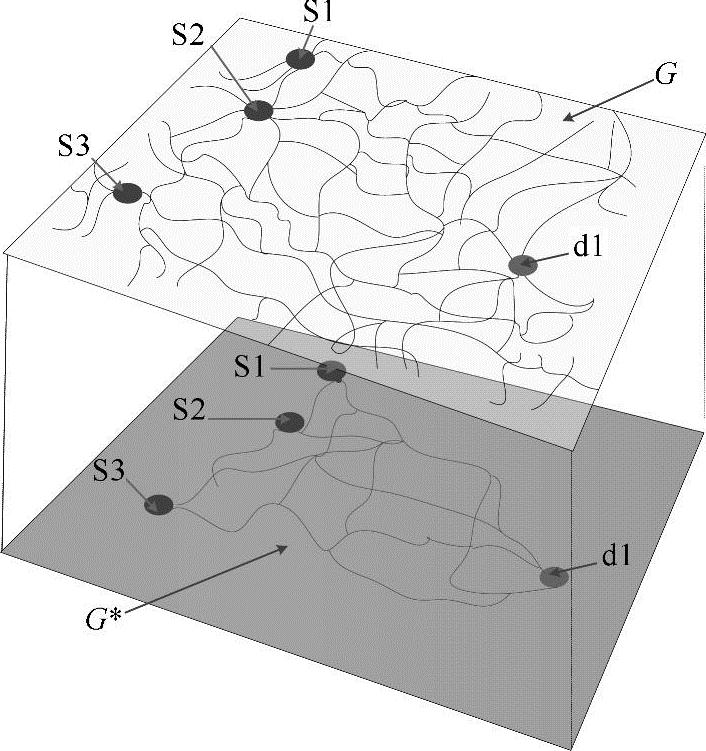
图4-4 交通应急疏散抽象拓扑图示例

另一方面，为了在进行交通疏散时使交通流规避危险点（如安全事故发生的地点），则需要将与该危险点连通的路段封锁以禁止交通车辆进入；在具体的算法设计中，可通过将该危险点所对应顶点（记为v_k）的出度设置为0实现，亦即

a_kl=0 （4-2）(www.xing528.com)

式中，l=1，2，…，n。由此，可进一步设置与v_k相关的路段权重属性量化值：

w_kl=+∞ （4-3）

根据式（4-2）和式（4-3）完成A=A（G）=[a_ij]_n×n和W=W（G）=[w_ij]_n×n的更新设置，进而采用Dijkstra-Yen算法计算获得每一个疏散源点到每一个疏散目的地的前K条最短路径，以此构成交通应急疏散抽象拓扑网络G^*[14-16]。

（3）疏散交通流最优分配模块的设计与实现

设每一个疏散源点与每一个疏散目的地之间有K条最短路径作为疏散交通流的诱导分配路径，在交通应急疏散抽象拓扑网络G^*的基础上，采用整数线性规划结构设计疏散交通流最优分配模型。令P_ijk表示分配到第i个源点与第j个目的地之间第k条路径上的疏散交通流量；d_ijk表示第i个源点与第j个目的地之间第k条最短路径的路段总权重值，其可通过对构成该路径的所有路段的权重值求和得到；S_i表示G^*中源点i处待疏散的车辆数，D_j表示G^*中疏散目的地j可容纳的车辆数；同时，记i=1，2，…，n；j=1，2，…，m，则疏散交通流最优分配模型为

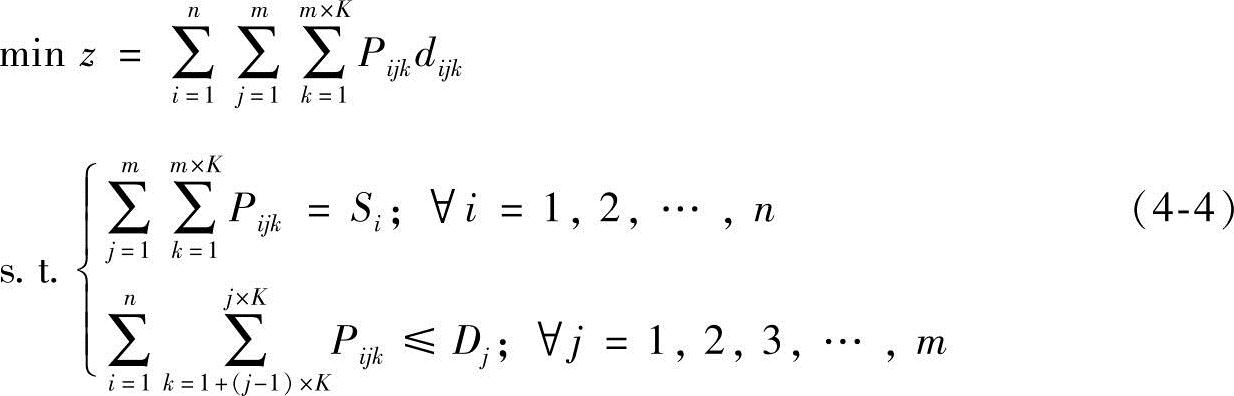
通过求解上述模型式（4-4），即可得到疏散到交通应急疏散拓扑网络G∗上的最优交通流分配方案。为了求解模型式（4-4），引入PSO算法^[17]。采用惩罚函数的方法处理模型式（4-4）中不等式和等式约束，将模型转化为无约束最优化模型：

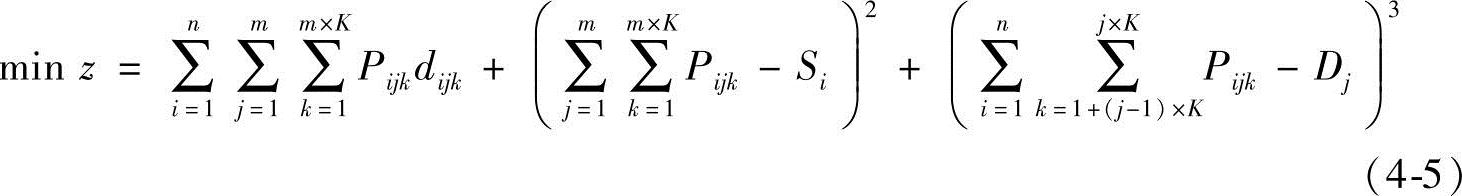
由于在模型式（4-5）中，决策变量P_ijk为非负整数，需要改进设计PSO算法中粒子位置和速度更新公式以使PSO算法适用于求解无约束整数规划模型。记非负整数k表示PSO算法迭代步骤，φ₁为满足在（0，1）之间均匀分布条件的随机参数，λ₁为满足在[0.5，1）之间均匀分布条件的随机参数；第l个粒子在第k迭代步骤的位置矢量为X_l（k）=[P_ijk]，速度矢量为V_l（k），该粒子历史最优位置矢量为X^g_l（k），全局最优粒子位置矢量为X^g（k）；初始步骤k=0时粒子的位置矢量可通过随机方法生成，位置矢量和速度矢量迭代更新通过式（4-6）和式（4-7）实现，且每一迭代步骤完成粒子位置矢量的更新后利用式（4-8）对各个分量执行向上取整操作：

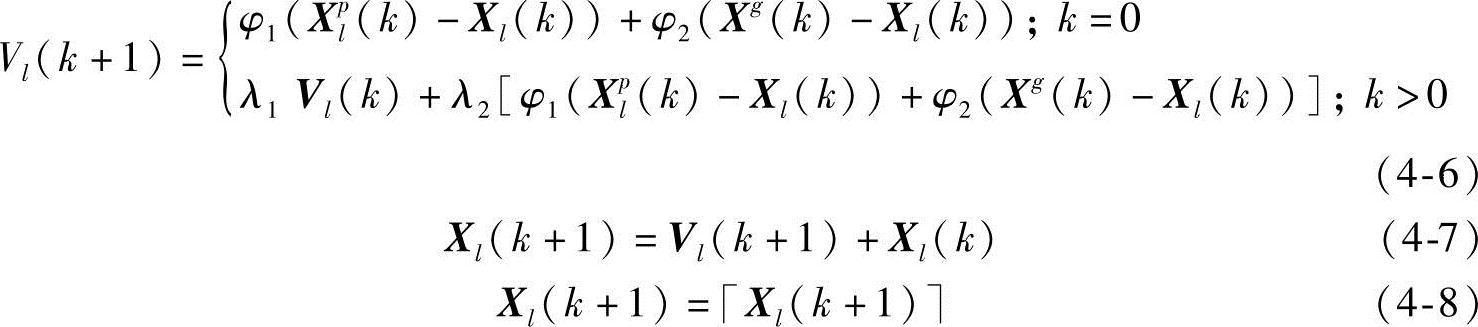
式（4-6）中，φ₂=1-φ₁且λ₂=1-λ₁；式（4-6）、式（4-7）和式（4-8）中，l=1，2，…，M，M为设定的粒子总数；[X]表示对矢量X的各个分量进行向上取整操作。

为了将上述疏散交通流最优分配模型应用于实际嵌入式系统当中，在Eclipse集成开发环境中采用跨平台应用软件的面向对象程序设计语言Java实现PSO求解算法模块，从而确保模块功能具备较好的跨平台系统通用性和移植性。

（4）疏散路径信息发布模块

基于车联网实现车载终端联网无线数据传输，可采用TCP/IP协议下的Socket编程实现应急交通流疏散路径信息的发布功能模块。通过疏散交通流最优分配模块计算获得从疏散源点到疏散目的地的疏散路径，进一步通过车联网向车载终端发布该路径信息诱导车辆安全疏散。