【摘要】:本章的研究所进行的实验,是建立在一种比较理想的情况下,也就是交通量不大且不考虑交通信号干扰,从而基本上可以用泊松分布拟合数据[10]。一个时间段内到达一个区域的空车数量n符合泊松分布,P(λ)。图3-10 空车到达时间间隔分布与候车时间分布基于以上分析,乘客的候车时间的概率密度如下:乘客的候车时间的概率分布如下:以上就是通过出租车的空车到达时间间隔的概率分布模型来推断导出的乘客候车时间的概率分布模型。
本章的研究所进行的实验,是建立在一种比较理想的情况下,也就是交通量不大且不考虑交通信号干扰,从而基本上可以用泊松分布拟合数据[10]。
一个时间段内到达一个区域的空车数量n符合泊松分布,P(λ)。空车到达时间间隔t服从指数分布P(t)=λe-λt(图3-10)。则有以下两条推论:1)假设,在一个时间段内,乘客均匀随机等概率地到达并候车。则乘客落入时间长度为t间隔的概率密度取决于时间间隔的概率和时间间隔的长度。时间间隔的概率越大,时间间隔的长度越长,则乘客落入其中的概率越大。2)乘客在时间间隔t内,极端情况下需要t时间可以搭乘出租车。从而可知,乘客落入时间长度为t间隔的概率密度正比于时间间隔本身出现的概率密度P(t)与时间间隔长度t之积P(t)t。而如果是极端的情况,乘客候车时间WT=t的概率密度f(Δt)与P(x)x成正比。
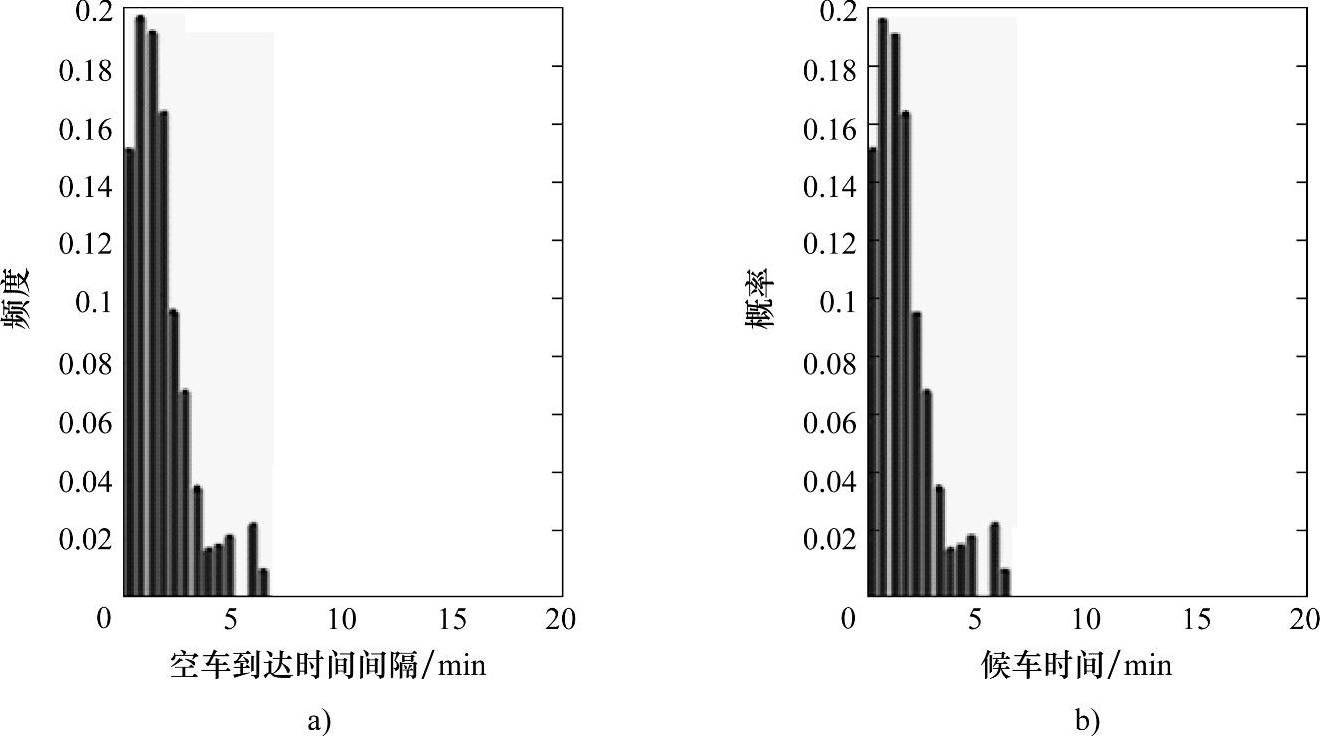
图3-10 空车到达时间间隔分布与候车时间分布
基于以上分析,乘客的候车时间的概率密度如下:(https://www.xing528.com)
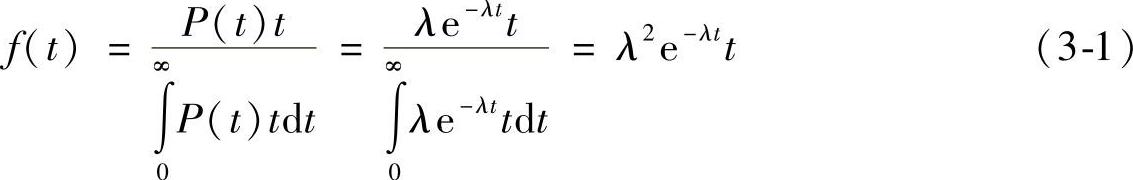
乘客的候车时间的概率分布如下:
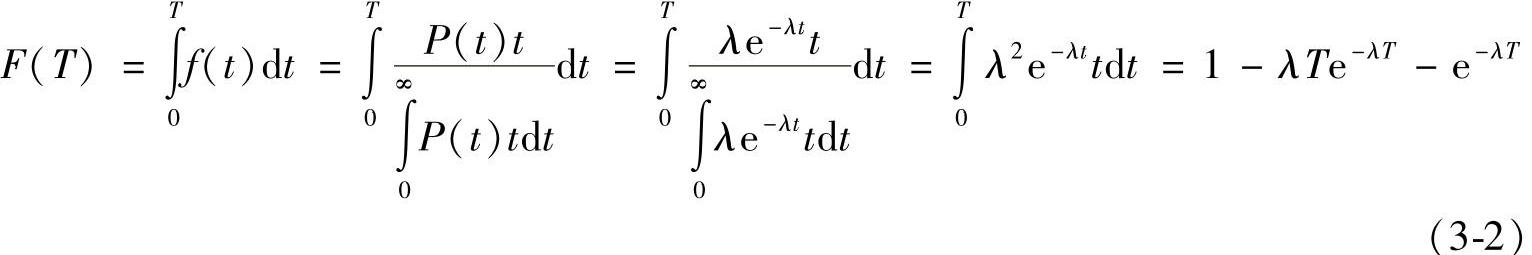
以上就是通过出租车的空车到达时间间隔的概率分布模型来推断导出的乘客候车时间的概率分布模型。如果给定一个乘客候车概率阈值,预测算法就可以计算在某区域某时段乘客以此概率阈值能够等候到空载的出租车所需要的时间。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




