根据仿生学的特征,本书将交通环境类比于鱼群的生存环境,多个车辆在道路上行驶类比于鱼群集体行进,借鉴鱼群的自组织效应。此外,鱼群的感知系统和整个群体内信息的传播系统在多车协同中可以通过ITS中的车车(V2V)通信来模拟。
为了探究将鱼群群集行为模型扩大应用到车流的移动中的可行性,我们结合了社会力的理论及社会力模型来建立多车协同移动模型来描述在车车通信条件下多车协同行驶和多车协同避撞。
本节建立了多车协同移动模型(CMVMM)来描述在同一段道路上协同行进的多辆车,此外,考虑到每个车辆个体对周围环境和周围邻车的感知,并通过短程通信(DSRC)来实现。在此情况下,每辆车可以通过基于专用短程通信(DSRC)的车辆自组织网络(vehicular ad hoc network)来实现车车信息交互。除此之外,车辆跟驰行为也通过力学的角度抽象出来,并且模型包含了影响整体行进的实际的力,包括目标的吸引力、障碍物的斥力、车道的约束力,以及车辆群体间的保持群体行进的引力和保持安全距离的斥力。
该模型的一个主要目的是详细说明车辆无线通信技术对多车协同避碰和避障行为的影响,并且可以从多车协同的自组织特性角度给出深入的分析。此外,该模型还可以用于分析在有内部通信的情况下多车协同的安全性和评估有无通信在不同场景下对交通通行效率的影响。在CMVM模型中,车辆的集合为VV={1,2,…,n},其中车辆总数为n,且n>2。在这些车辆中我们将目标车辆称为i,其邻车记为j并满足条件∀i≠j∈VV。此外,我们用矢量pi(t)=[xi(t),yi(t)]T来表示车辆i在t时刻的位置。本章假设将所有车长相同并记为L,在此基础之上我们将所有的车辆简化视为半径为ri=L/2的圆(图2-5),如果车辆进入其他车辆的半径ri之内,将视为碰撞。此外,将Ri(Ri>ri)定义为车辆个体间的作用范围圆的半径(图2-6),凡是在车辆i作用圆内的车辆之间相互影响比较明显,它们间相互的引力和斥力作用来保证它们像鱼群个体一样不会碰撞有紧密的集体行进,超出此范围的相互作用就比较弱,暂且忽略不计。
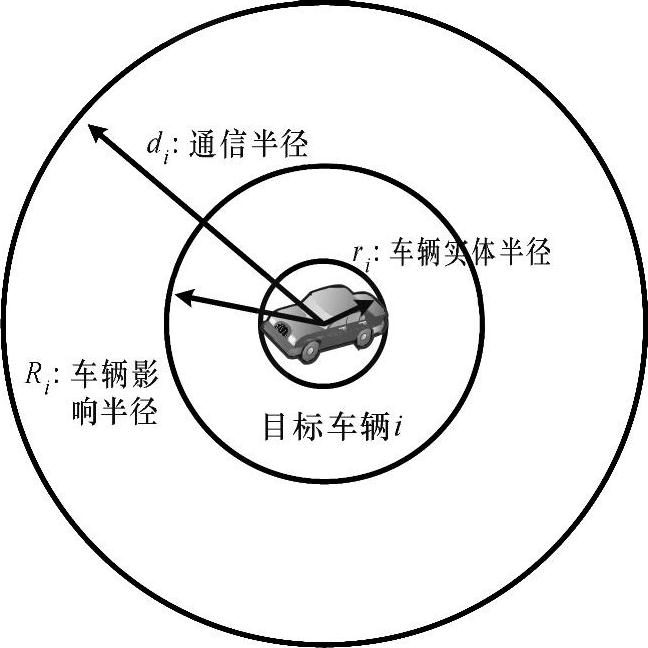
图2-5 车辆个体示意图
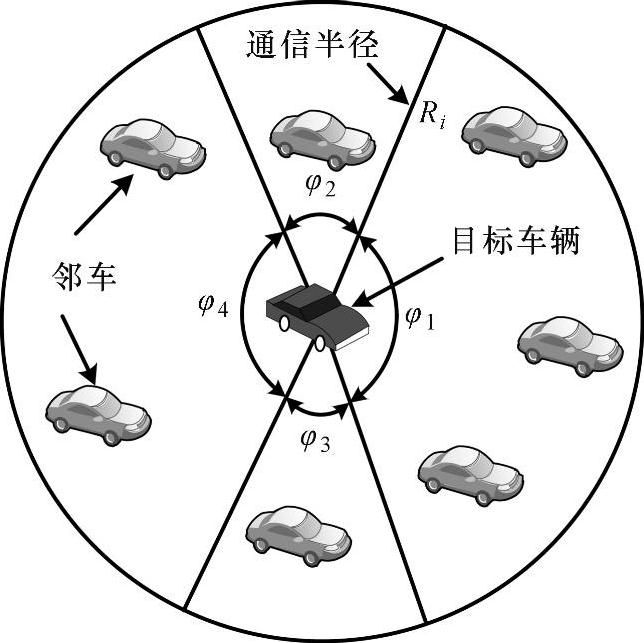
图2-6 目标车及其邻车
根据研究可知,鱼群中的个体间的协同是通过感觉系统来实现的,每个个体从鱼群内部和外界环境中感知信息并传递信息,信号会在整个群体中传递,并和群体做出的反应融为一体作为完整的一组响应[7]。鱼群中成员越多就会收集到更多的信息,信息越丰富,整个群体做出的决定也会更合理。
类比于此,假设本章中的车辆都配备车载传感器和实现车车通信的设备来模拟鱼群的感知和通信系统。本章中车车通信范围都相同,记为di(图2-5)。为了刻画多车协同的运动特征,目标车辆i在t时刻所受的合力如下
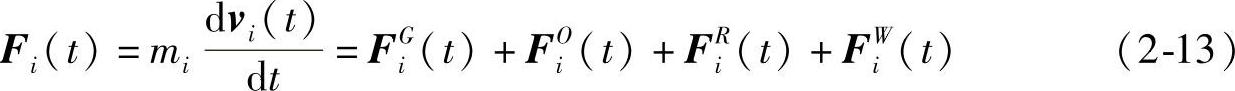
其中,目标车辆i的质量记为mi,影响车辆行进的主要作用的力在下面会分别进行说明:
1)FiG(t)表示目的地对目标车辆的吸引作用,提供车辆行进的动力。车辆如果没有受到干扰,车辆会保持期望速率v0i沿着期望方向ei(t)行进。由此,可记期望速度为
v0i(t)=v0iei(t) (2-14)
但是在实际情况中,车辆会有必不可少的加速减速或者躲避行为导致偏离期望速度,所以,记在t时刻车辆的实际速度为vi(t),但是目标的吸引作用始终会有把车辆的速度拉回到期望速度的趋势,所用冗余时间记为τi。
因此,将目的地引力作用表示为
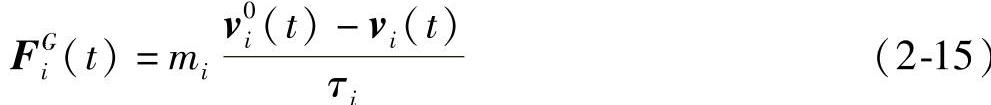
该作用力用来表示提供给车辆的动力,能保证车辆沿着目的地的方向行进。
2)FiO(t)表示障碍物边界对车辆的排斥作用,本章将道路上的障碍物、车祸现场和道路维修现场等需要绕开的区域统称为障碍物,这些情况是在道路上很常见的,会影响交通通行的场景。多车作为一个整体协同避撞对提高交通安全性和车辆通信效率有很大的意义和作用。
障碍物Oki的集合用ℕ={0,1,2,…,m}来表示,其中m≥0且k∈ℕ.同样假设障碍物Oki是半径为rkO的实心圆,进入半径rkO则视为与其碰撞。此外,障碍物Oki的圆心的位置用矢量pkO=[xkO(t),ykO(t)]T表示,pi(t)-pkO表示车辆i与其最近的障碍物Oki圆心距。图2-7给出了障碍物Oki的实体半径、作用范围以及与车辆间的关系的示意图。当车辆接近障碍物Oki并且pi(t)-pkO小于车辆通信范围时,即障碍物进入车辆的探测范围,则车辆开始受到障碍物的斥力作用,车辆i必须与障碍物保持一定的安全距离来避免碰撞。

图2-7 障碍物的作用范围
综上,障碍物Oki的斥力作用表示为
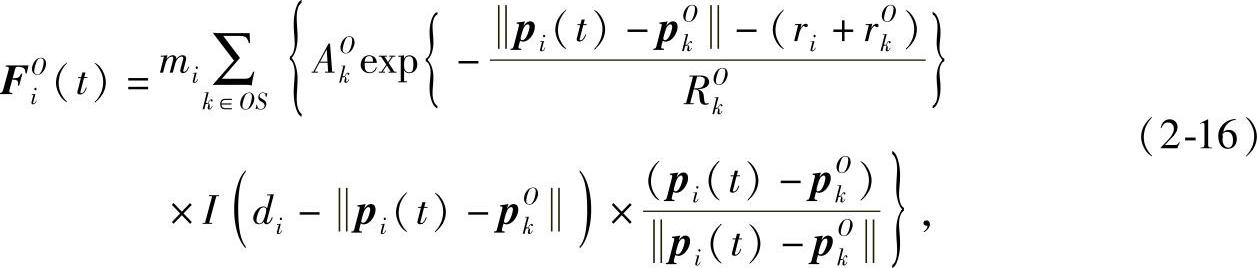
式中,AkO是常数, 一项是障碍物的圆心指向车辆的质心的方向单位向量。该斥力是障碍物和车辆圆心距的单调递增函数。
一项是障碍物的圆心指向车辆的质心的方向单位向量。该斥力是障碍物和车辆圆心距的单调递增函数。
其中示性函数定义如下:
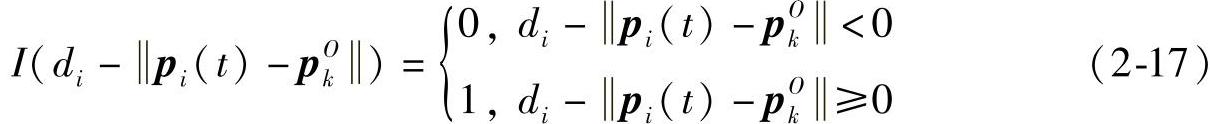
当di>pi(t)-pkO时,车辆i进入障碍物斥力作用范围,与此同时,斥力FiO(t)开始作用。若di<pi(t)-pkO,车辆i并不能探测到障碍物,不考虑该障碍物对其的影响。此外,若rkO<pi(t)-pkO时,视为车辆和障碍物碰撞,避障失败。(https://www.xing528.com)
该力是描述车辆整体外部行为的力,接下来的描述的力是车辆组内部个体间的作用力。
3)FNi(t)表示车辆群体内目标车辆i与在其影响范围内邻车j之间的相互影响作用。从实际情况出发,周围不同位置的邻车对目标车辆的影响作用是不同的,以Ri为半径的车辆作用圆,依据角度φk(k=1,2,3,4)分为四个区域,区域φ1是车辆前方区域,将φk区域内的车辆记为jφk∈Nφk,Nφk(k=1,2,3,4)是每个区域中邻车的总量。根据实际经验,前方的车辆会比两侧车辆以及其后方的车辆影响作用更大些,本章用系数ωk(k=1,2,3,4)来区分每个区域内的邻车对其影响作用的大小,其满足ω1>ω2=ω3>ω4。
车辆间既有组成群体的凝聚力,又有避免相互碰撞保持安全距离的排斥力。车辆间的引力和斥力会随着两车间的距离变化而变化,距离越近,小于安全距离dsij(t)则斥力起主要作用,大于安全距离则引力起主要作用。因此,用以下函数来刻画两车(i,j)间距离与力的关系:
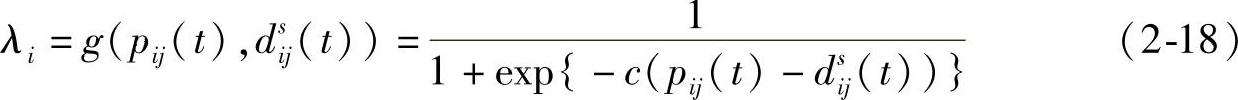
其中,c为常数,且有pij(t)给出为

在多车协同行进的过程中,依据交通模型中常见的安全距离给出期望车间距为[8]
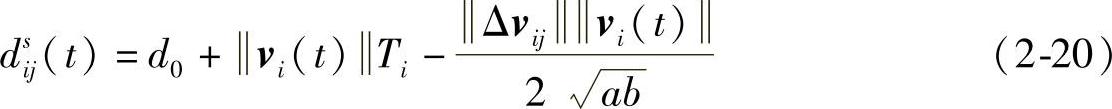
d0是两车最小的停车间距,如交通拥堵时候两车在不碰撞的情况下的停车间距,Δvij是车辆i和j的速度差,a和b分别为最大加速度和最大减速度,Ti是总反应时间,包括驾驶人的反应并制动的时间tr和车辆间无线通信时信息传递的延误时间td:
Ti=tr+td(2-21)
鱼群的个体之间会有使其集群的引力也有使其相互避免碰撞的斥力,多车行进的群体里也同样是相似的原理。
引力表示如下:
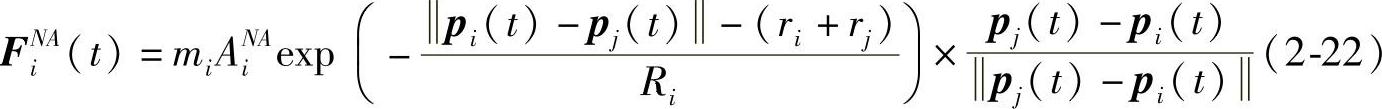
斥力表示如下:
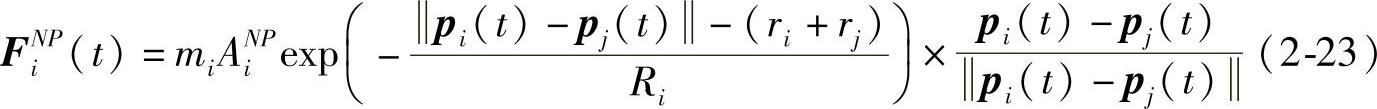
其中ANiA、ANiP、μ2、μ3均为系数,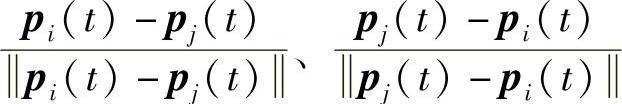 是每个力的单位方向矢量。
是每个力的单位方向矢量。
综上所述,车辆i所受到的群体内部作用力表示为

若pi(t)-pj(t)≤(ri+rj)时,则表示车辆间发生碰撞。
4)最后一个作用力,FiW(t)是考虑到车辆群体和鱼群的差别,给出的依据实际情况的表示车道约束作用的力。其定义如下
FiW(t)=f(t)ef(2-25)
其中
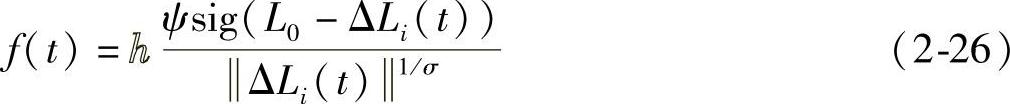
且

其中,ef表示车辆行驶下一步的目标方向。车辆在行驶过程中必须遵守交通规则,如有偏离车道,也会重新回到车道行驶,力FiW(t)是刻画车辆偏离车道后会将其重新“拉回”到车道内的作用。hh和σ是常系数,ψ则给出如下:
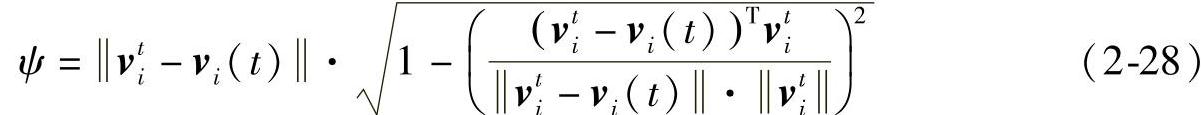
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




