车联网系统：实测数据分析

（1）广义极值分布模型

上面提到，在网络传输中数据包越小其时延中传输试验所占的比例越大，因此在试验中为了获取传输时延的分布，对于典型的64B的数据包传输做了大量的数据，并对其进行了数据分析，而吞吐量和时延抖动都是基于时延所获得的，因此本书将研究的重点放在时延分析上。本书发现得到的数据分布图与广义极值分布（Generalized Extreme Value Distribution，GEV）模型十分接近，因此以GEV模型为基础进行了改进，得到了适应实际数据分布的分布模型，进而更加精确地描述了DSRC时延分布的特点^[23]。

在概率分布中，广义极值分布模型是基于极值理论发展而来的一种概率分布模型，是与Gumbel、Fréchet和Weibull，也就是我们所熟知的Ⅰ型、Ⅱ型和Ⅲ型极值分布相结合的连续概率分布，通过极值定理的GEV是独立同分布的随机变量序列极大的唯一可能的极限分布。尽管这样，GEV经常被用来作为一个近似随机变量的长（有限的）序列的极大值进行建模。

在应用程序的某些领域的广义极值分布称为费雪蒂皮特分布，它们因概述如下三个功能形态而得名。但是使用这个名称有时也仅限于指Gumbel分布的特殊情况。

广义极值分布有它的累积分布函数^[12]：

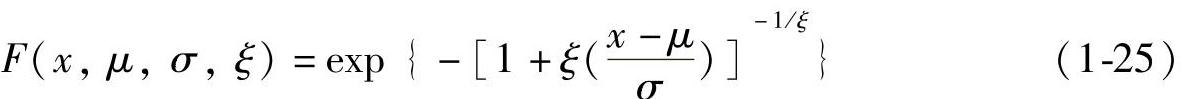
式中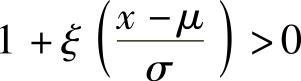，，μ∈R是位置参数，σ＞0是规模参数，ξ∈R是形状参数，因此当ξ＞0时，给出的累积分布函数表达对于x＞μ-σ/ξ是有效的，而当ξ＜0时，给出的累积分布函数表达对于x＜μ-σ/ξ是有效的。在第一种情况下，在最低点它等于0；在第二种情况下，在最高点它等于1。对于ξ=0的情况并没有给出正式定义的函数而是利用ξ→0时的函数极限得到的：

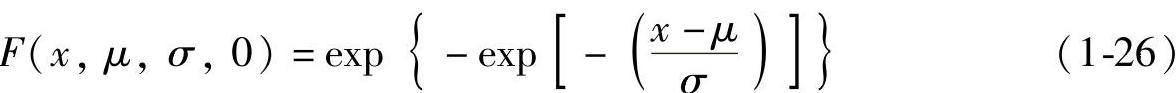
x上没有任何的限制。

因此概率密度函数是[13]

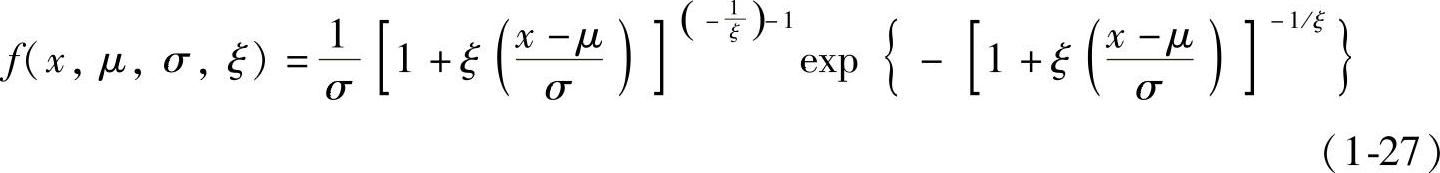
同样地，当ξ＞0时，给出的累积分布函数表达对于x＞μ-σ/ξ是有效的，而当ξ＜0时，给出的累积分布函数表达对于x＜μ-σ/ξ是有效的，相关的范围之外的密度是0，而当ξ=0时，概率密度函数如下：

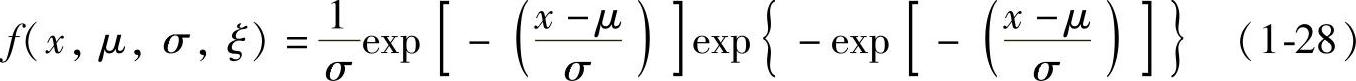
如图1-44所示，即μ=0，σ=1时的不同ξ下概率密度分布图，与试验数据分布非常相似。

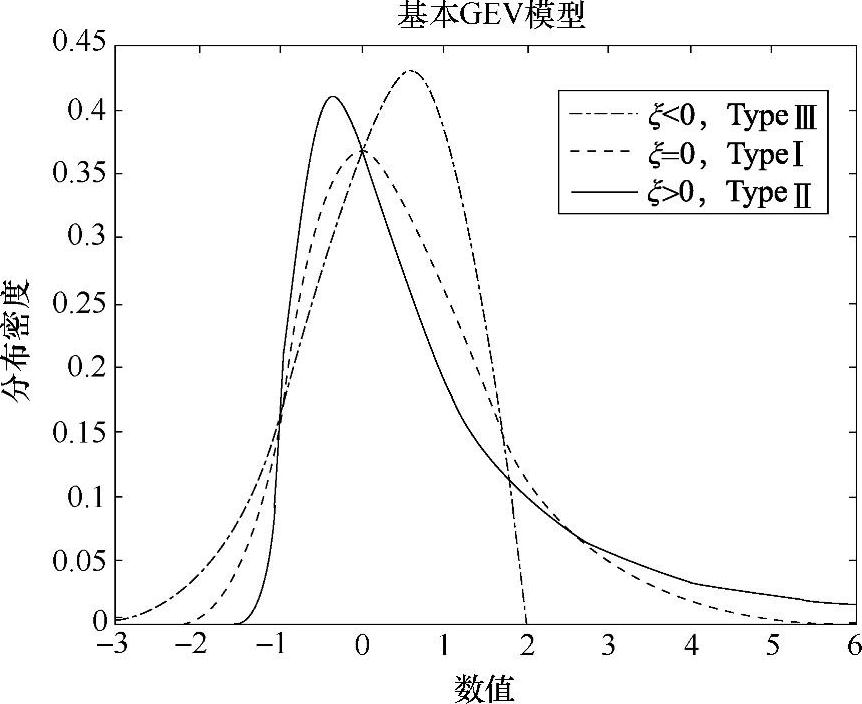
图1-44 μ=0，σ=1时的不同ξ下概率密度分布

（2）基本GEV模型拟合结果

试验数据的均值Ex=0.4721，标准偏差为0.0309，利用极大似然估计法对GEV模型进行计算，从而得出所需的μ、σ、ξ参数，进而使用GEV模型进行拟合。

极大似然估计：

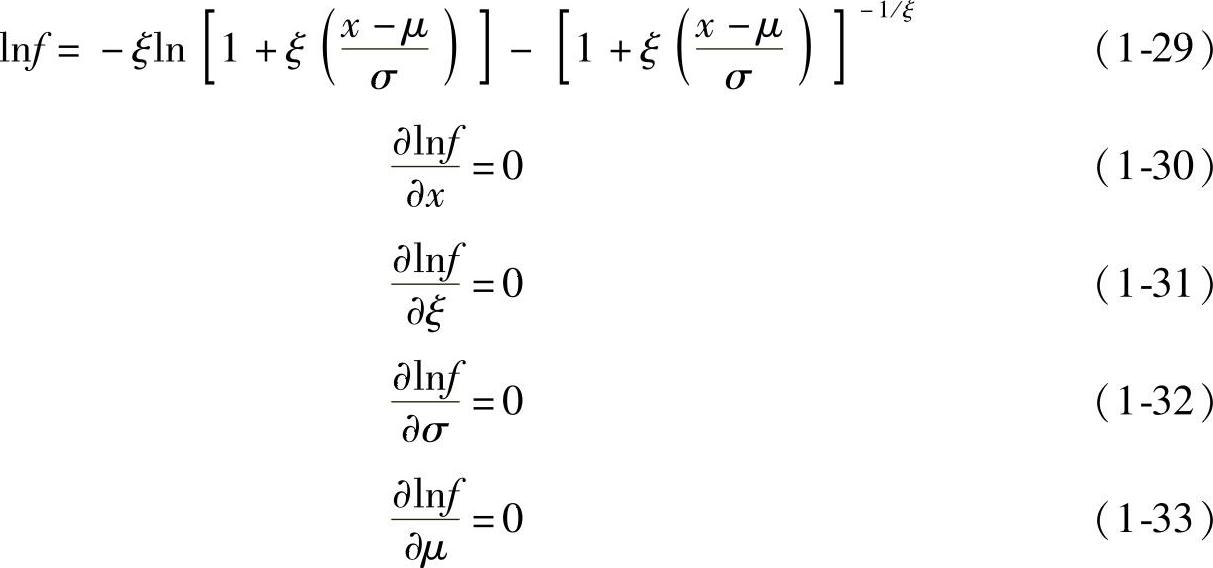
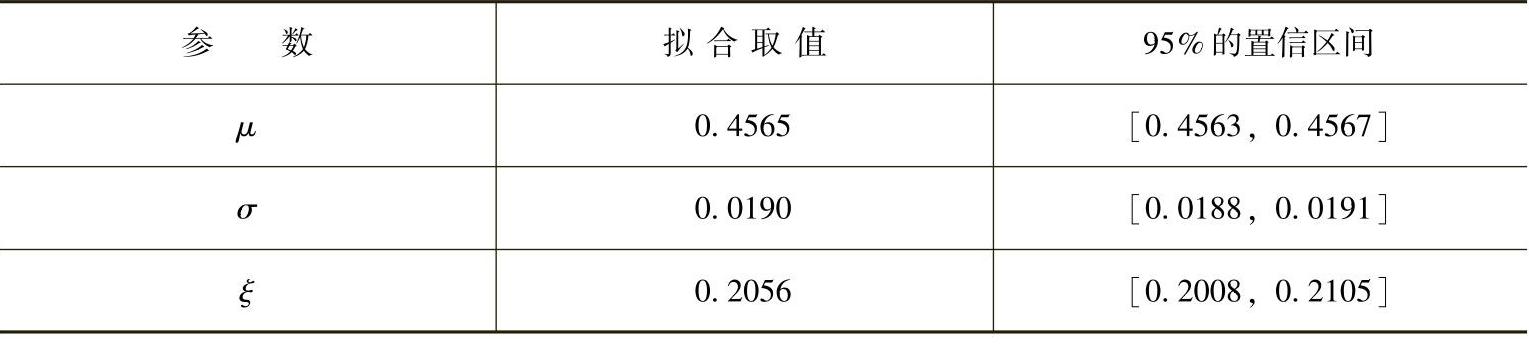
在置信度区间为95%时，极大似然估计的结果见表1-2。

表1-2 参数估计结果

如图1-45所示，虚线为基本的GEV模型下的拟合曲线，它基本上能够拟合实测的数据，和实测的数据达到了较好的匹配，但此模型仍然可以进一步改进。

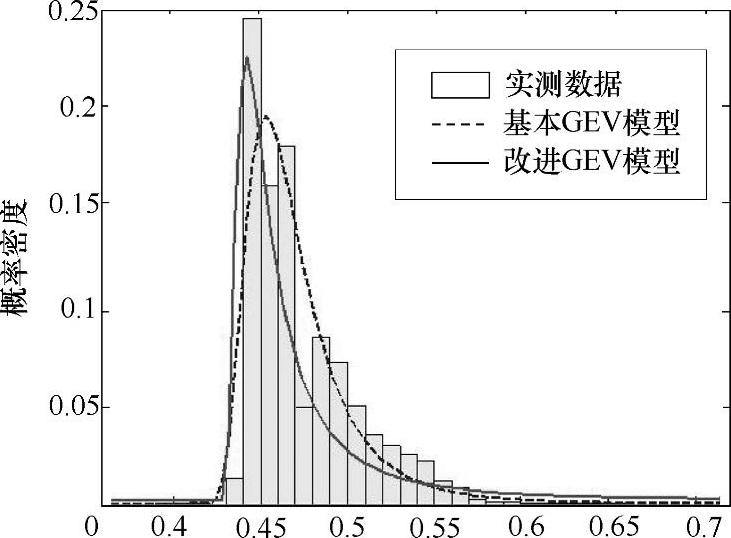
图1-45 实测数据与基本GEV模型传输时延对比

（3）改进模型

前面使用基本的GEV模型对实验数据进行了刻画，下面将对模型进行进一步改进，并使用非线性最小二乘估计法得到最优模型。

对于原始的GEV模型，改进成如下的模型^[14]：(www.xing528.com)

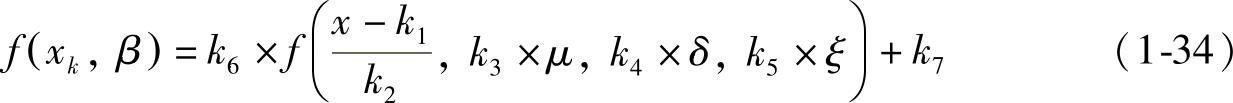
β即向量（k₁，k₂，k₃，k₄，k₅，k₆，k7），接下来使用非线性的最小二乘法来获得β的最优解。

非线性最小二乘法是以误差的平方和最小为准则来估计非线性静态模型参数的一种参数估计方法。设非线性系统的模型为y=f（x，β），式中y是系统的输出，x是输入，β是参数（它们可以是向量）。

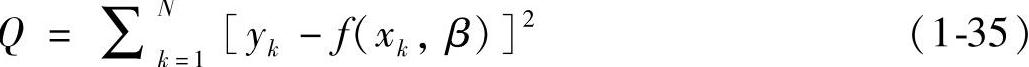
这里的非线性是指对参数β的非线性模型，不包括输入输出变量随时间的变化关系。在估计参数时模型的形式f是已知的，经过n次试验取得数据（x₁，y₁），（x₂，y₂），…，（x_n，y_n）。估计参数的准则（或称目标函数）选为模型的误差平方和非线性最小二乘法就是求使Q达到极小的参数估计值。

接下来使用Levenberg-Marquardt算法进行计算，从而获取Q的最小值和β的最优解。

Levenberg-Marquardt算法就是为了在数学和计算机计算中解决非线性最小序列的解法，在最小二乘曲线拟合方面显得尤其明显^[15]。正如许多其他的算法一样，Levenberg-Marquardt算法也是一个迭代过程，为了启动算法，首先需要设置一个向量β的初始值，

在只有一个最小值的情况下，β=（1，1，1，1，1，…）已经可以有较好的效果，而在有多个极小值的情况下，则必须要对最终值有一个比较接近的估计才能实现。在每一步迭代中，β会被β+δ所取代，为了确定δ，函数f（x_i，β+δ）可以约等于它的线性估计^[16]：

f（x_i，β+δ）=f（x_i，β）+J_iδ （1-36）

其中

J_i即f关于β的梯度。

在最小平方和上，S（β）作为S关于δ的梯度将会为0。上面对于f（x_i，β+δ）的一阶近似使得

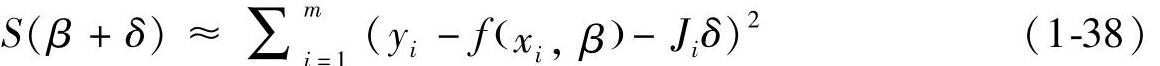
或者是向量表达：

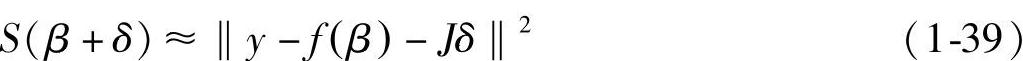
关于δ求导并将结果设为0得

（J^TJ）δ=J^T[y-f（β）] （1-40）

其中，J是雅可比矩阵，J的行i和J_i的相同，相对地，f和y是以f（x_i，β）和y_i组成的向量，这是一个可以解出δ的线性方程组。Levenberg的分布就是为了用一种阻尼版本来代替这个公式：

（J^TJ+λI）δ=J^T[y-f（β）]其中I是单位矩阵，作为δ的增量来对估计参数向量β。非负的衰减向量λ在每一步迭代中反复调整，如果S的衰减比较快，那么一个更小的值就会被使用，然后引导算法靠近高斯牛顿算法，其中如果有一步的迭代没有给出足够的衰减，λ会增加并且靠近梯度下降的方向，注意S对于δ的梯度等于-2（J^T[y-f（β）]）T，因此，为了λ的大值，这一步取在近似梯度的方向。如果计算步骤的长度δ或者是序列和的衰减β+δ低于预设的阈值，迭代将会停止，而最终的参数向量β则看成问题的解。

Levenberg的算法在阻尼因数λ过大时会导致反向的（J^TJ+λI）不起作用，Marquardt提出根据曲率计算出梯度的每个部分从而在原本梯度较小的方向上有较大的移动，这就避免了在小梯度上的缓慢收敛，因此，Marquardt使用J^TJ的对角元素组成的对角矩阵来替代单位矩阵I，形成了Levenberg-Marquardt算法^[17]：

（J^TJ+λdiag（J^TJ））δ=J^T[y-f（β）] （1-41）

基于Levenberg-Marquardt算法，在Matlab上进行编程获得了β向量值如下：β=（3.0111，0.8449，0.9908，119.2557，-0.0018，-0.0038，1.0001）；拟合结果如图1-46所示。

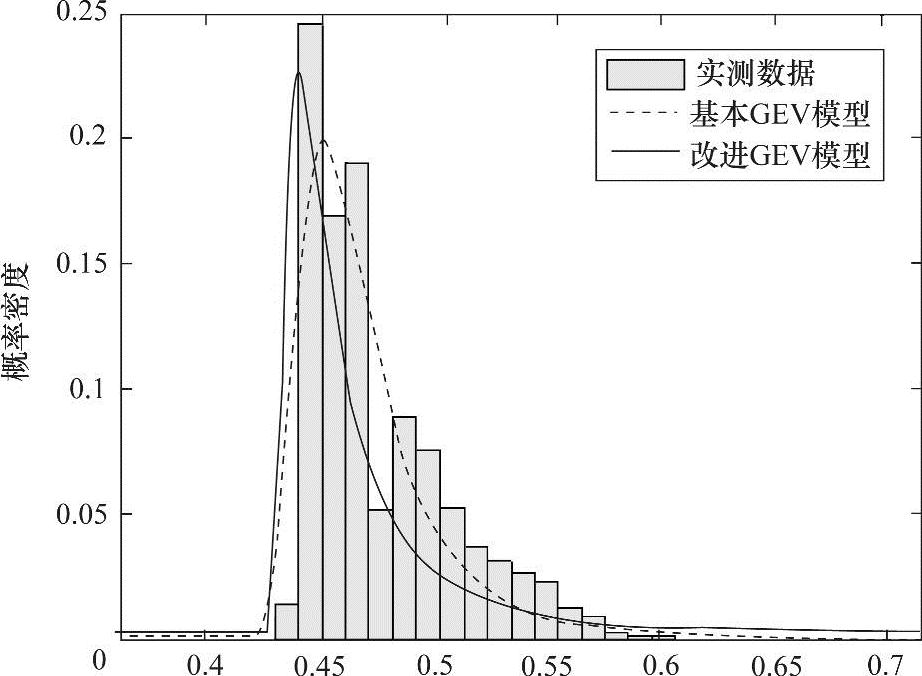
图1-46 实测数据与两种模型传输时延对比

如图1-46所示，灰色柱状图为试验测得的端对端传输时延的试验数据的频率分布图，虚线即改进后的GEV模型，它的拟合效果明显优于实线，能够更好地刻画端到端的传输时延，至此，试验所得的时延的数据已经可以用本书所改进的GEV模型进行模拟，为DSRC时延分布的刻画提供了较好的理论工具，而这种由实际数据所得的模型比其他模型也更有说服力。

利用改进后的GEV模型，可以评估DSRC网络服务质量（QoS），验证网络运营商与客户之间的服务等级协议[18]，也能用来研究有效的DSRC通信协议的拥塞控制机制，根据获得的时延模型，预测时延的变化情况来调整传输策略，这样使得到的算法、设定的参数更符合实际网络运行规律^[19]，也可作为度量DSRC网络路径性能的指标（Metric），用以进行路由优化和路由动态更新，还可用作DSRC网络优化的依据，据其制定负载均衡策略，同时能给新的网络应用，如CDN（Contention Distribution Network）提供支持^[20]。