汽车车身噪声、振动控制的调制度、波动度、粗糙度

调制度、波动度和粗糙度是一个概念。调制是两个不同频率和/或不同幅值的波叠加后的效果。由于调制频率不一样，人的主观感受也不一样，就有了波动度和粗糙度之分。当调制频率低时，人感受到的波像波浪一样，这时的调制度叫波动度。当调制频率高时，人感受到的波很粗糙，像颠簸一样，这时的调制度叫粗糙度。

1.调制度

当两个频率不同或者幅值不同的纯音波叠加在一起的时候，就产生了调制效应。假设两个纯音信号分别表达为

两个信号合成后，表达为

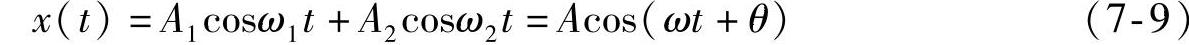
式中，A为两个信号的合成幅值；ω为合成信号的角速度，分别表达为

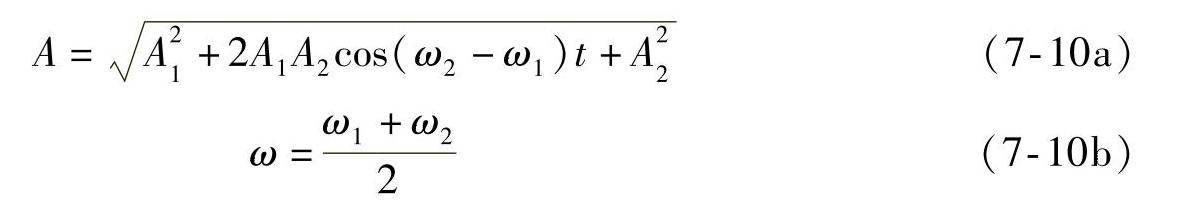
为了画出两个单频信号的叠加情况，这里给出例子A₁=10，f₁=20Hz；A₂= 15，f₂=23Hz。图7-9所示为这两个单音信号的时域和频域图。

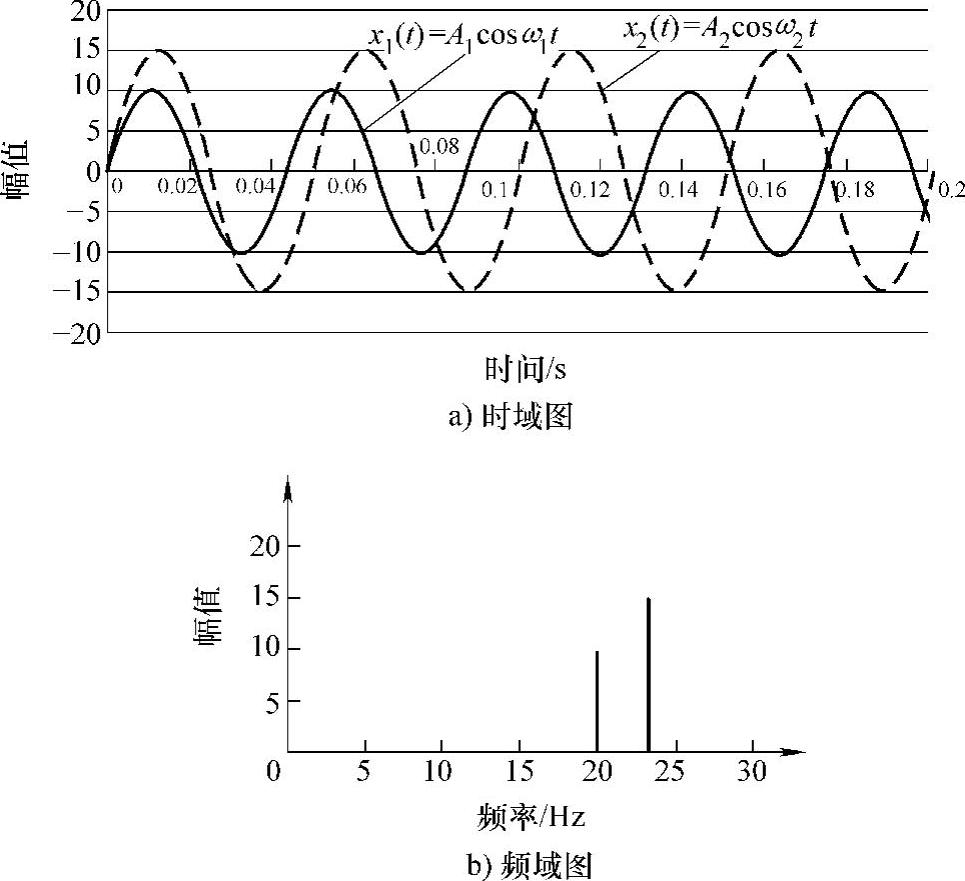
图7-9 两个单音信号的时域图和频域图

根据式（7-9），绘制出两个信号叠加的波形，如图7-10所示。

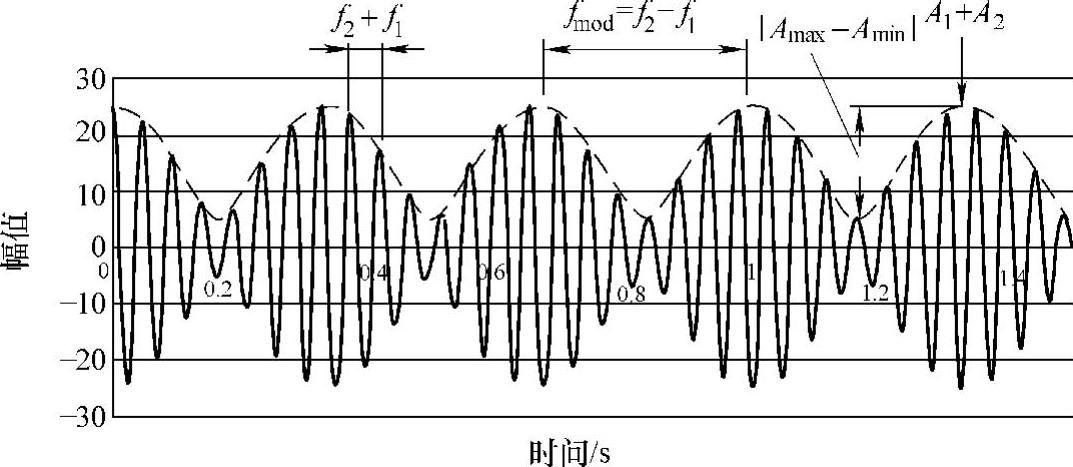
图7-10 两个频率和幅值不同的单音信号的叠加图

两个信号叠加后，会以新的幅值和频率进行波动，这种现象被称为调制。调制信号的最大幅值和最小幅值分别为：A_max=A₁+A₂，A_min=A₁-A₂。调制信号在A_max和A_min之间波动。将调制的最大值和最小值之间的差值称为调制深度，用D表示

调制信号从最大值到最小值变化，再从最小值到最大值变化，这种变化呈现周期性，用调制频率f_mod来表示，为

考虑两种特殊情况：

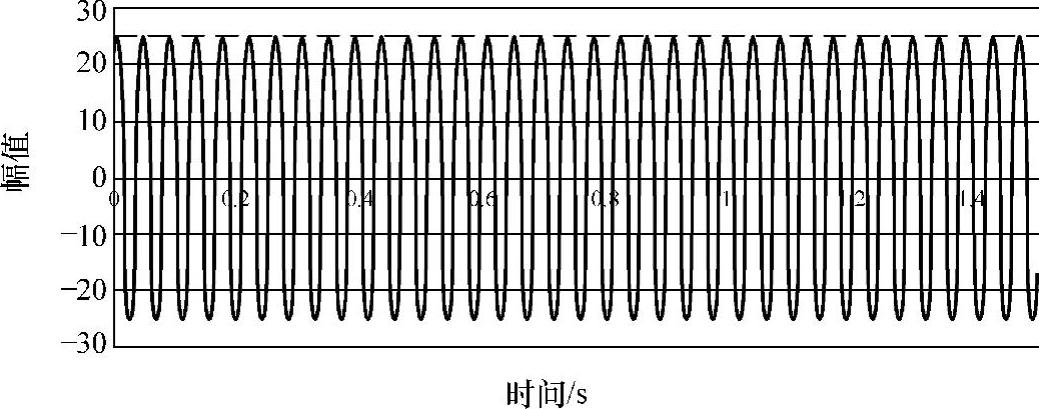
①两个信号的频率相同而幅值不同，即f₁=f₂，A₁≠A₂。对于上述例子，两个信号叠加后的曲线如图7-11所示。由于频率相同，叠加后仍然是一个单音信号，只是幅值是两个信号幅值的叠加。对这种情况，不存在调制现象。

(www.xing528.com)

图7-11 频率相同而幅值不同的两个信号叠加

②两个信号的幅值相同而频率不同，即A₁=A₂，f₁≠f₂。对于上述例子，得到叠加后的曲线如图7-12所示。由于幅值相同，调制的最小幅值为零，即A_min=A₁-A₂=0，最大幅值为单一信号幅值的两倍，即A_max=A₁+A₂=2A₁。

按照调制频率的大小，调制度又分为波动度和粗糙度。当调制频率小于20Hz 时，叠加的声音或振动表现为波动（Fluctuation），相应的调制度就成了波动度。当调制频率为20～300Hz时，叠加的声音或振动表现为粗糙（Roughness），相应的调制度就成了粗糙度。当调制频率大于300Hz以上时，人可以分辨两个频率的声音，就把它们当成纯音信号。

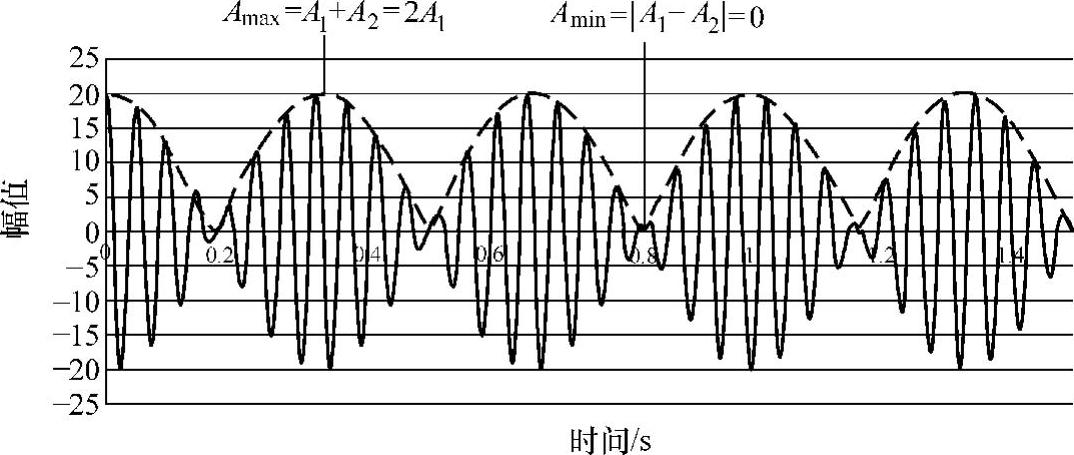
图7-12 幅值相同而频率不同的两个信号叠加

2.波动度

波动度是描述调制频率为0.5～20Hz的声音或振动变化带给人的听觉感受。声音波动最典型的例子就是两个不同频率的音叉放在一起，它们分别发出各自频率的声音。当它们的频率接近，人听到的信号就是两个纯音叠混的声音，声音时高时低，形成一种波浪起伏的状况。

再举一个在不平路面上驾驶汽车的例子来说明振动波动度。汽车自身以一个频率作垂向运动，假设将起伏路面看成是一个正弦波，它有一个频率。人感受到的垂向运动是这两个运动的叠加，即两个频率的运动形成了调制效果。由于路面起伏的频率和汽车垂向运动的频率都很低，而且频率差比较小，行驶在这样的路面就有随波荡漾的感觉，好像被海上的波浪缓慢托起又被慢慢地放下，即感受到的是“波动”。

波动的强弱可以用波动度来表示。波动度的单位用Vacil表示。频率为1000Hz和声压级为60dB的纯音，其调制频率为4Hz以及调制深度为100%的调幅信号，定义这样的波动度为1Vacil。波动度F的计算公式为

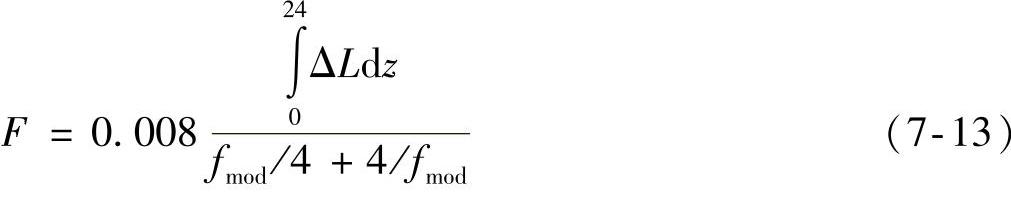
式中，f_mod是调制频率；ΔL是掩蔽深度，通过信号的响应谱计算得到。掩蔽深度是人感受到的声音幅值的变化，它比实际声音的变化要缓和。掩蔽深度和调制深度是两个概念，掩蔽深度可以从时域掩蔽效益中得到。

影响波动强度的因素有波动的频率、声压级大小和波动的深度。调制频率为4Hz时，波动度最大；调制频率小于4Hz时，波动度随着调制频率的增加而增加；调制频率大于4Hz后，波动度随着频率的增加而减小，如图7-13所示。波动度越大，人听起来越不舒服。

3.粗糙度

当调制频率大于20Hz，人就分辨不出声音强度的每次变化，而听到的声音是“粗糙”的。下面以汽车通过缓冲带为例来说明振动的粗糙度。缓冲带由很多彼此之间距离很近的条带组成，这样缓冲带路面的“频率”很高，这个频率与汽车垂向频率相差比较大，使得“调制频率”很高。行驶在这样的路面上，人没有上下起伏的感觉，反而觉得路面“粗糙”。

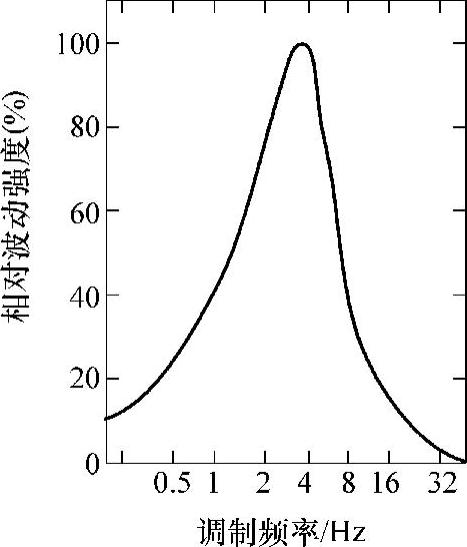
图7-13 波动度随调制 频率的变化曲线

粗糙度是声音信号快速调制带给人的听觉感受。粗糙度的调制频率范围从20Hz到300Hz，单位是Asper。对1000Hz、60dB的纯音进行调制，调制频率为70Hz，调制深度为100%幅值，被调制后的声音的粗糙度定义为1Asper。粗糙度可以用式（7-14）计算：

从式（7-14）来看，影响粗糙度的因素有调制频率和掩蔽深度。70Hz时，粗糙度最大。粗糙度越大，听起来就越不舒服。

粗糙度不限于纯音的调制，宽带、窄带声音的调制也可以产生粗糙度。