汽车车身噪声与振动控制：原点动刚度

1.动刚度的概念

对于线性系统，用施加在系统上的力除以位移，即得到了刚度。刚度是系统固有的特征，与外界施加的力和响应没有关系，即“静止”状态就存在的，所以称之为静刚度。在静止状态下，在系统上施加力并测量位移，就可以得到静刚度。式（5-20）中的k就是单自由度系统的静刚度。

在外力的作用下，系统运动起来，其刚度特性随着输入的频率而发生变化。将速度和加速度与位移的关系代入式（5-20），得到系统的刚度为

此时的刚度是激励频率（ω）的函数，即刚度是随着频率而变化的，而不是一个固定值。此时的刚度被称为动刚度，其幅值为

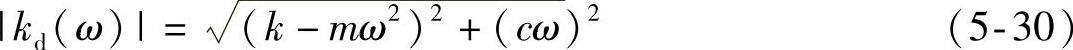
动刚度取决于系统的质量、阻尼和静刚度。图5-30显示了一个单自由度系统的动刚度曲线，它对应的质量为2kg，阻尼为10N·s/m，静刚度为2000N/m。

式（5-29）或式（5-30）中，当系统静止时，即ω=0时，k_d=k，即动刚度就是静刚度。因此，可以说静刚度是动刚度的一种特殊情况。

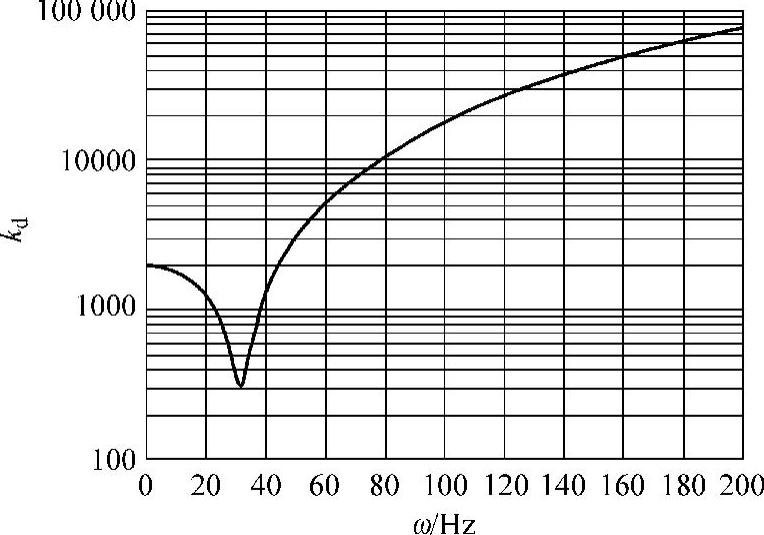
图5-30 一个单自由度系统的动刚度曲线

将式（5-30）和式（5-23）进行比较，发现这两个公式的表达式是一样的。也就是说，动刚度就是位移阻抗，即

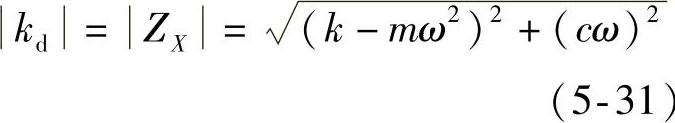(www.xing528.com)

2.原点动刚度

在一个系统中，若激励力的点和响应点是同一点，则得到的刚度就被称为原点动刚度。“原点”是指响应和激励为同一点。对图3-45这样的单自由度系统，激励点和响应点是同一点，因此，式（5-29）表示的动刚度就是原点动刚度。

多自由度系统或者连续体系统中，施加力的点和响应点可能很多，如图5-31所示。

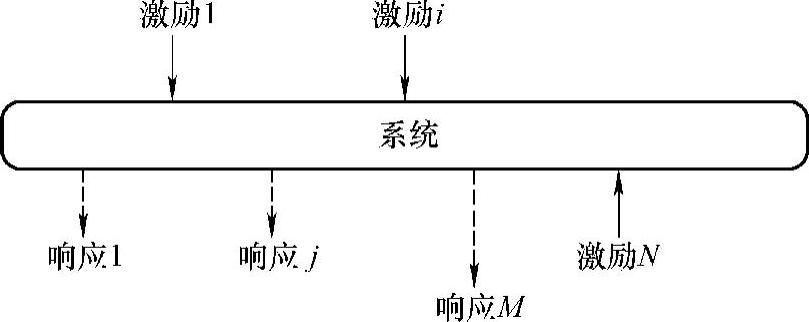
图5-31 多自由度或连续系统的激励点和响应点示意图

在第二章模态分析基础部分，详细介绍了多自由度的模态分析理论以及单点激励和单点响应的传递函数。式（2-55）给出了响应点（l点）与激励点（p点）之间的传递函数，即

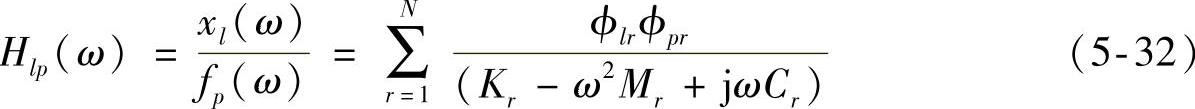
式（5-32）就是单点激励下的系统位移导纳。

当响应点与激励点为同一点时，假设都是在l点，就得到

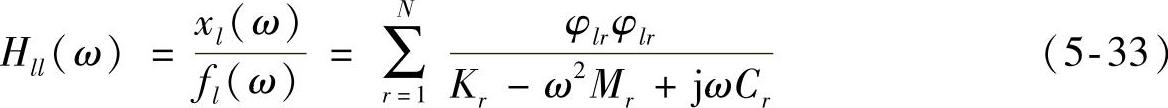
式（5-33）就是同一点的位移导纳，或者称为原点导纳。由于导纳与动刚度（或阻抗）互为倒数，因此原点动刚度就是原点导纳的倒数。根据式（5-33）得到了原点导纳，就得到了原点动刚度。