汽车车身噪声与振动控制：统计能量分析

1.能量平衡

系统的统计能量分析是以系统间流入、流出和损耗能量之间的平衡为基础的。图4-75表示一个系统由两个耦合在一起的子系统组成。

对第一个子系统来说，它的能量流由四部分组成：

①外界输入的功率：外界对子系统做的功，用Π₁来表示。

②第二个系统输入到第一个系统功率，即第二子系统通过流出的形式而损耗的能量，Π₂₁，表示为

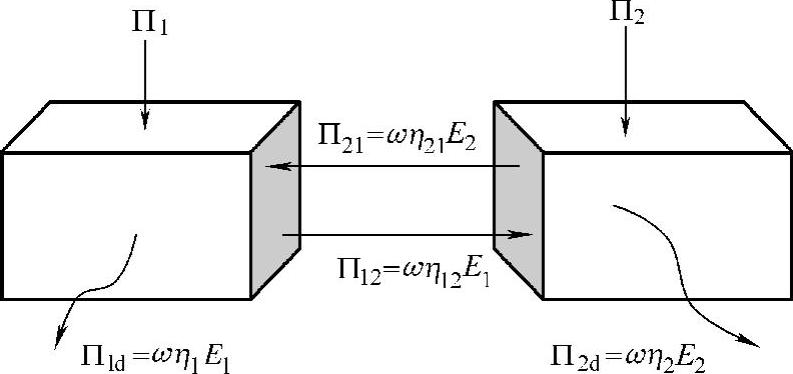
图4-75 由两个子系统组成的耦合系统

式中，η₂₁为第二个系统对第一个系统的耦合损耗因子；E₂为第二个系统的能量。

③内部消耗的功率：由于系统存在阻尼，内部要消耗掉一部分能量，并转化成其他形式的能量。对于黏性阻尼而言，其消耗的功率为

式中，c₁为第一个系统的阻尼系数；η₁为第一个系统内部损耗因子；E₁为第一个系统的能量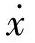； 为振动速度；ω为子系统的固有频率。

④第一个系统输出到第二个系统的功率，即第一个系统通过流出的形式而损耗的能量，Π₁₂，表示为

式中，η₁₂为第一个系统对第二个系统的耦合损耗因子。

对于一个保守系统来说，流入的能量等于内部消耗的能量加上流出的能量。对第一个子系统来说，流入的功率包括外部输入的功率和从第二个系统输出的功率。因此，这个子系统的能量平衡方程可以表达为

将式（4-55）～式（4-57）代入式（4-58），得到(www.xing528.com)

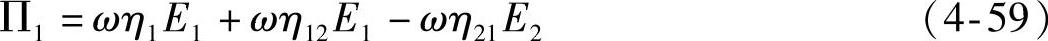
2.系统的能量平衡方程

图4-75中的第二个系统也可以写出与第一个系统同样的功率平衡方程式，表

达为

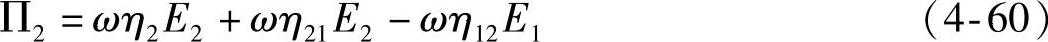
式中，Π₂是外界对第二个系统的输入功率；η₂是第二个系统的内部损耗因子。

将式（4-59）和式（4-60）写在一起，就得到图4-75所示的由两个子系统组成的整个系统的功率流方程组，表示为

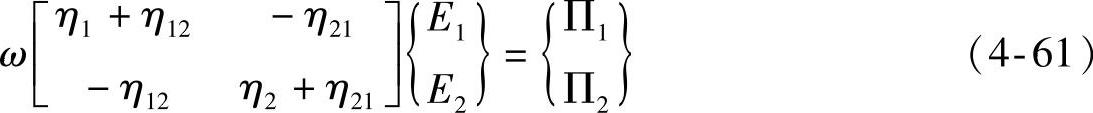
将这种功率流的分析方法推广到由N个子系统组成的系统，如图4-76所示。对于每个系统，输入的能量等于内部消耗的能量加上对外输出的能量。

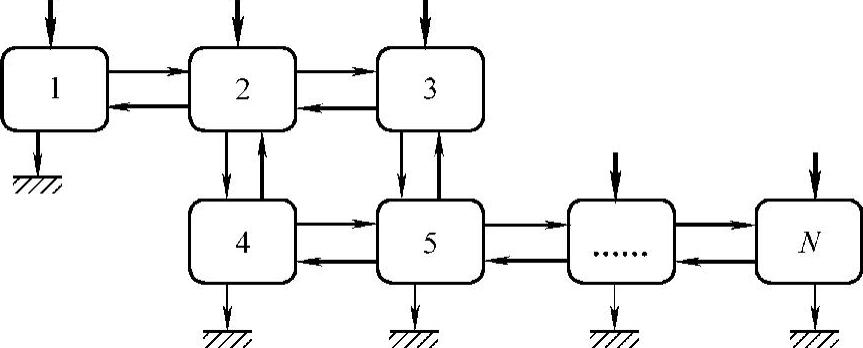
图4-76 由N个子系统组成的系统

对于N个子系统的大系统，功率流方程组表示为

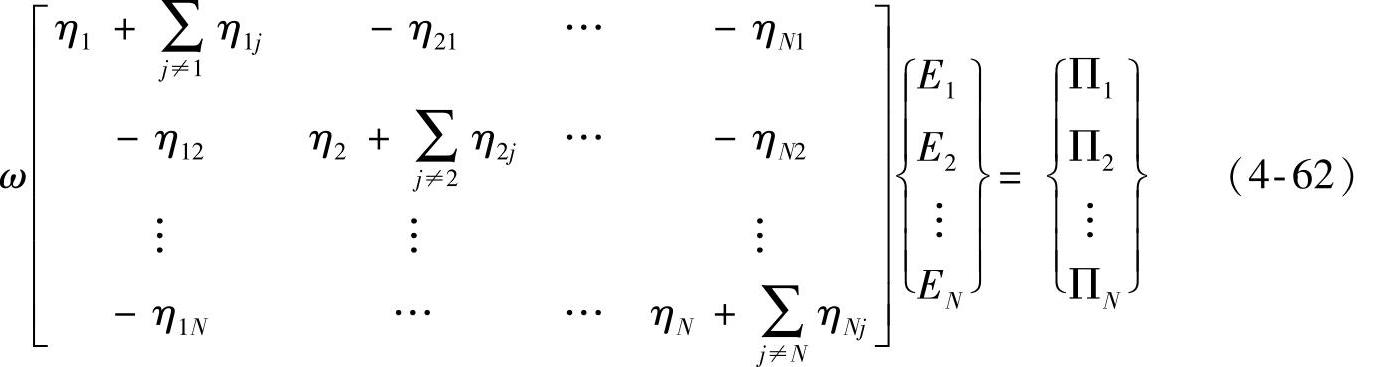
式（4-62）可以简单地改写成

从式（4-62）或式（4-63）来看，给定了输入功率{Π}和系统的损耗因子[η]，就可以求得系统的能量{E}。得到了系统的能量之后，根据式（4-52）或式（4-54），就可以得到系统的振动速度或声压。