汽车振动控制：统计能量分析简介

统计能量分析是从“统计”和“能量”两个角度来分析振动和噪声问题。下面先解释一下这两个概念。

1.统计的概念

图4-74为一个典型的汽车车内噪声振动响应图谱。在低频时，响应（如速度、声压等）的曲线非常清晰，每个峰值的大小和对应的频率都可以清楚地读出来。在中间频率时，响应的峰值密度增加，有的可以辨别出来，有的就难以分辨了。进入高频区域，响应的峰值非常密集，每个峰值的大小和对应的频率已无法分辨。

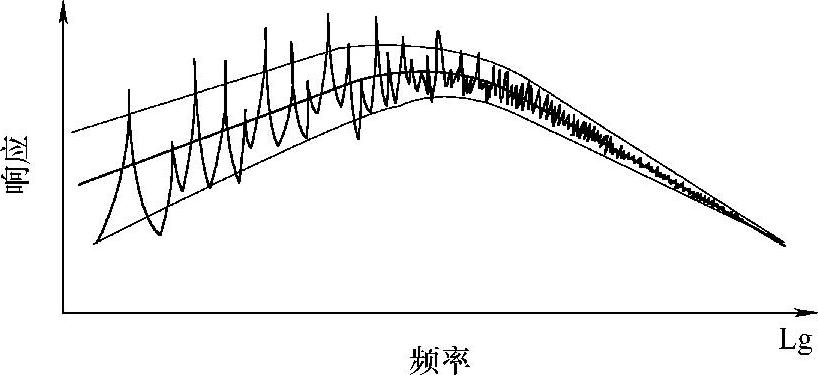
图4-74 典型的汽车车内噪声振动响应图谱

对低频响应，由于可以清晰地分辨出响应，因此，就可以用传统的、清晰的解析方法来分析，得到每个位置、每个频段具体的速度值和声压值等。在高频区域，由于模态密集，无法得到每个响应具体的值，因此，只有用统计的方法来描述某个频段的响应平均值。对于高频密集的振动与噪声信号，“统计”就是很好的分析方法。

2.能量的概念

当一个系统的振动模态非常密集时，系统的动能和势能相当。系统的总能量（E_V）可表示为：

式中，M为系统的质量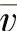； 为平均速度。

将式（4-51）改写为(www.xing528.com)

式（4-52）用来表征结构振动的速度与系统能量之间的关系。

对于一个声腔系统来说，当声腔模态密度足够大时，声能（E_S）与声腔空间的平均声压 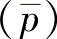的平方成正比，表达为

式中，V_i为声腔的体积；ρ₀为空气密度；c为声速。

式（4-53）改写为

式（4-54）用来表征声音的声压信号与系统能量之间的关系。

由式（4-52）和式（4-54）可知，对于模态密度高的高频系统，表征振动信号的速度和表征声音信号的声压可以用能量来表示。即对于高频密集的振动与噪声信号，“能量”是一种很好的分析方法。

将“统计”的分析方法和“能量”的分析方法结合到一起，来分析高频噪声和振动问题，就是统计能量分析的基础。