阻尼模型及其在汽车振动控制中的作用

1.阻尼模型的种类

车身上存在阻尼的地方很多，如车身板件自身的阻尼、阻尼材料的阻尼、隔振元件带来的阻尼等。车身阻尼可以分为三类：第一类是结构本身的内部阻尼，如车身板、黏弹性材料等；第二类是相邻部件之间摩擦产生的阻尼；第三类是运动时受到的空气阻尼。

为了研究结构和材料的阻尼，人们建立了很多阻尼模型，包括黏性阻尼模型、结构阻尼模型、比例阻尼模型等。与车身阻尼分类相对应，阻尼模型也分成三类：

第一类是结构体阻尼模型，主要有黏性阻尼模型、迟滞阻尼模型和结构阻尼模型。车身板结构、阻尼材料等属于此类。本章重点介绍黏弹性阻尼模型。

第二类是干摩擦阻尼模型，主要是库伦阻尼模型。库伦阻尼是描述具有相对运动或者有运动趋势的物体界面间的阻尼。摩擦力（F_d）与表面的正压力（N）成正比，与运动的方向相反，与速度幅值无关，即F_d=-μN，μ为摩擦系数。车身金属板之间、金属板和橡胶之间、连接部位等地方都存在着摩擦力。

第三类是空气阻尼模型，主要是空气动力阻尼模型。汽车运动时，受到空气的阻力，这属于外部阻力。其阻力（F_d）与汽车运动速度的平方成正比，即

式中，β为空气摩擦阻尼系数，v为车速。

由于本章讲述的阻尼是车身板的阻尼，阻尼是用来控制板结构的振动和噪声辐射，所以涉及的阻尼属于第一类。

下面用单自由度系统来描述带阻尼的系统方程，如图3-45所示。系统的运动方程可以表达为

式中，F_d为系统的阻尼力；m为系统的质量；k为系统的刚度，x为系统的位移；f为外界施加的力。

应用图3-45的模型，下面就第一类阻尼模型（黏弹性模型、迟滞模型和结构阻尼模型）进行简单的描述。

2.黏性阻尼模型

黏性阻尼模型是所有模型中最常用的。黏弹性阻尼力与物体运动速度成正比，即F_d=c 其中c为阻尼系数。黏性阻尼模型表达为

引入临界阻尼c_cr的概念，即c_cr=2ω_n m=2√ km。ω_n=√k/m，为系统的固有频率。定义阻尼比（ξ）为

对自由振动的情况，式（3-54）改写为

工程中，绝大部分阻尼是欠阻尼，即0<ξ<1。求解方程（3-56），得到系统的自由振动响应为

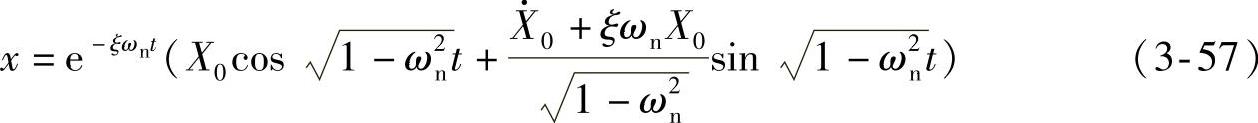
式中，X0是系统的初始位移值。(www.xing528.com)

图3-46表示这个欠阻尼系统自由振动的位移随时间变化的曲线。其振动幅值随着时间逐步衰减，起衰减作用的是阻尼比ξ。为了评价阻尼对幅值衰减的快慢，可以用相邻两个周期内振幅的对数比来表示，即对数衰减率δ：

图3-45 带阻尼的单自由度系统

图3-46 欠阻尼系统自由振动的位移随时间变化的曲线

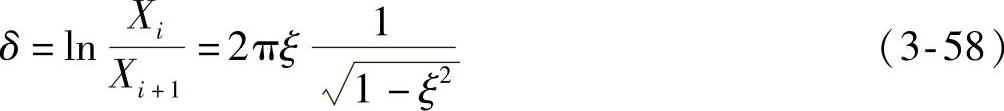
对小阻尼情况，即ξ<<1，式（3-58）可以简化为

从式（3-58）或式（3-59）可以看出，阻尼比决定了自由振动幅值的衰减快慢程度。

黏性阻尼模型是最简单的阻尼模型，阻尼力是线性的。应用这个模型来处理和求解振动运动方程非常方便，其他复杂阻尼模型可以经过等效能量损耗的方式来简化成黏弹性阻尼模型。

3.迟滞阻尼模型

黏性模型中，阻尼消耗的能量与振动频率成正比（将在本节后续内容介绍）。这个结论与一些结构振动能耗情况不相符，于是引入迟滞阻尼模型，以消除频率的影响，即迟滞阻尼力为F_d= h为迟滞阻尼系数。迟滞阻尼模型为

4.结构阻尼模型

结构阻尼是假设结构内部的阻尼与弹性力成正比，与速度同相位，即阻尼力为F_d=ivkx，其中v为结构阻尼系数。结构阻尼模型为

将式（3-61）中的阻尼力和弹性力合并为一项，形成总的内力，表示为

（1+iv）k被称为系统的复刚度。

5.比例阻尼和等效阻尼

当一个阻尼系统非常复杂时，采用以上的阻尼模型都难以得到振动的解析解，人们就将它们简化。通常被简化的模型有比例阻尼模型和等效阻尼模型。将阻尼看成是与质量和刚度成比例的关系，即将阻尼项分解到质量项和刚度项。由于质量项和刚度项满足正交原理，对多自由度系统来说，通过模态转换，方程可以变成离散的多个单自由度方程。