声腔模态理论分析和测量方法

1.声腔模态的计算

声腔模态的计算是基于经典的声学理论。在理想流体分析中有几条假设：流体是可以压缩的；介质是连续的和均匀的；没有声扰动的时候，介质是静态的；声音在传播过程中，介质的稠密和稀疏过程是绝热的；介质中传递的是小振幅声波，即声压远小于静态声压。在这些条件下，对介质建立三个方程：运动方程、连续方程和理想气体方程。将这三个方程结合在一起，就得到了三维声波方程

式中，c是声速；t是时间；p是声压，声压是时间和空间的函数，即p（x，y，z，t）；Δ 为拉普拉斯算符，表达如下：

对于封闭空间，空气有一定的质量、刚度和阻尼，通过Galerkin方法将式（3-23）的表达式进行离散化处理，将封闭空间分成若干个小的有限单元。流场内的波动方程可以写成有限元矩阵方程，为

式中，M_f为流体等效质量矩阵；C_f为流体等效阻尼矩阵；K_f为流体等效刚度矩阵。

与结构模态分析类似，求解式（3-25），可以得到声腔模态的声压分布形态，即声腔模态。式（3-25）中没有外界的激励输入，它是空腔自由运动方程。

声腔是非常复杂的结构，理论计算很难实现。计算声腔模态基本上是采用有限元方法。采用声学流体单元建立空腔的有限元模型，如图3-16所示，这是一个不带座椅的模型。单元越密，计算精度越高，但是计算时间就越长。在最大分析频率对应的声波波长内，保证有68个声学单元。

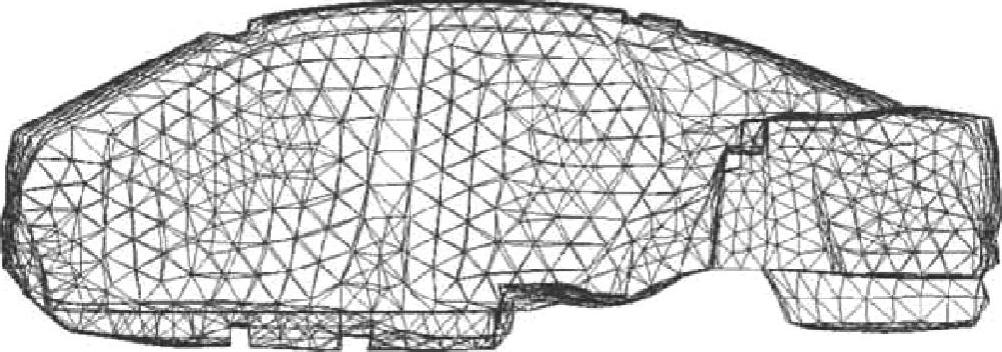
图3-16 车身空腔有限元模态（见彩插）

图3-17是某车没有座椅的前五阶声腔模态。图3-17a是第一阶声腔模态，频率为57Hz，其运动形式沿着汽车的纵向（x轴）传递。声压沿着x轴变化，有的声压变大，有的变小，而在中间某个部位声压为0。在同一横截面上，压力基本不变，即压力在横向（y轴）和垂向（z轴）方向压力不变。在纵向，声压的变化看上去像拉手风琴一样，因此，这种形状的模态称为纵向声腔模态。第一阶声腔模态称为第一阶纵向声腔模态。当声腔受到外界激励时，声压变化大的地方响应大，即灵敏度大，反之也一样。而在声压没有变化的地方，外界激励不引起任何变化，这些地方就形成了声腔模态的节点、节线和节面。

图3-17b为第二阶声腔模态，频率为102.5Hz，也是纵向模态，被称为第二阶纵向模态。其形状特征与第一阶声腔模态类似。

图3-17c为第三阶声腔模态，频率为119.5Hz。这个模态显示声压变化在纵向（x方向）和垂向（z方向）的很小，而主要是沿着汽车的横向（y方向），因此这种形式的模态被称为横向模态。由于是第一次出现的横向模态，因此图3.17c的模态被称为该车的第一阶横向模态。与纵向模态一样，其声压有的变大，有的变小，有的不变。不变的地方就形成了第一阶横向模态的节点、节线和节面。

图3-17d为第四阶声腔模态，频率为141.4Hz。这个模态显示声压在纵向x和横向y都有变化，其形态是纵横变化交织在一起。

图3-17e为第五阶声腔模态，频率为153.6Hz。通常，从第五阶模态起，它们的声腔模态变得复杂。

汽车声腔模态中，第一阶模态都是纵向模态；第二阶模态也是纵向模态（少数情况除外）；第三阶模态基本上是横向模态；第四阶呈现纵向和横向交织在一起的形式；从第五阶模态开始，高阶模态的形式就趋向复杂，形成了纵向、横向和垂向交织在一起的模态。

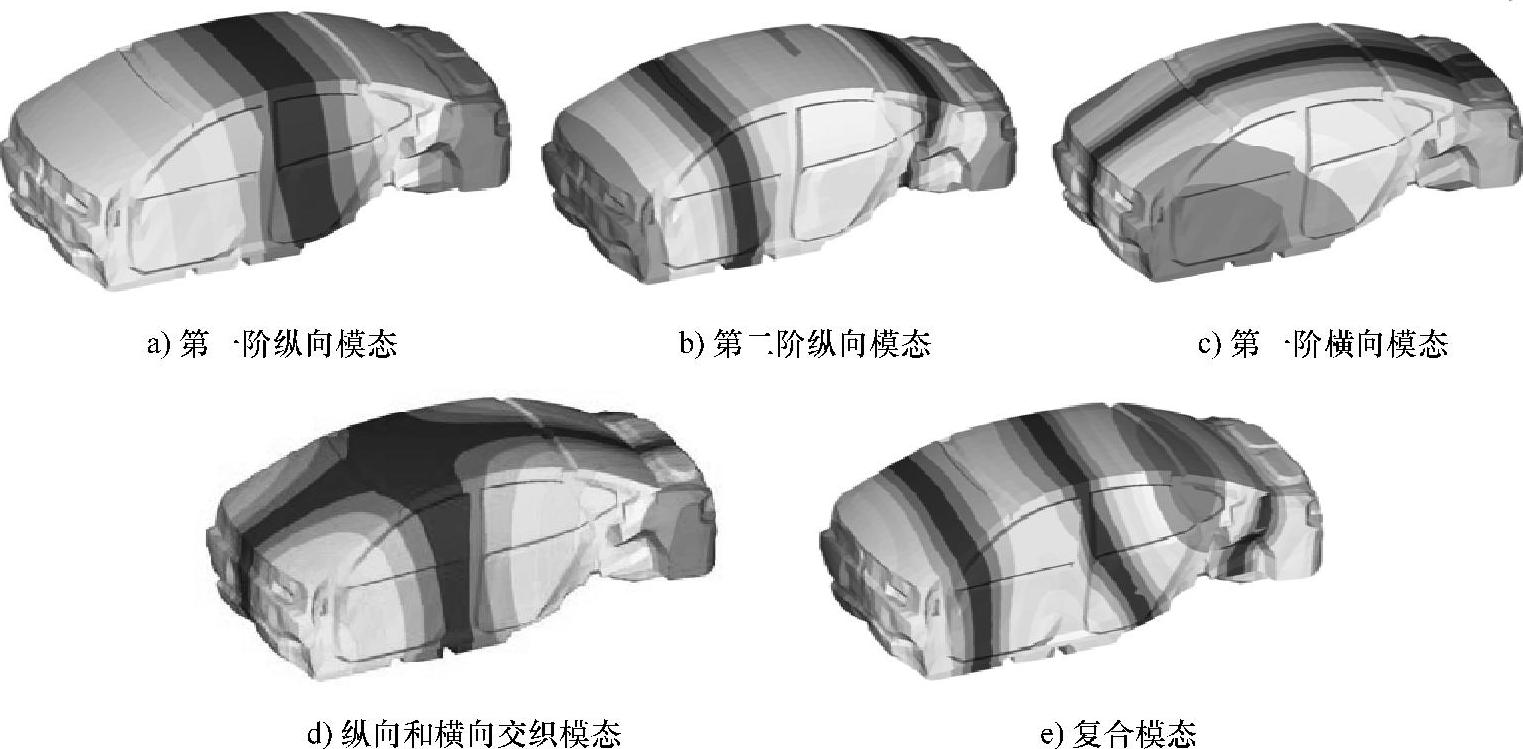
图3-17 某款车的前五阶声腔模态（见彩插）

2.声腔模态的测量

除了通过有限元分析获取声腔模态外，通过测量也可以得到声腔模态。

首先画出声腔轮廓，并确定好传声器布置的位置。将一系列传声器安装在车内，传声器之间的距离为2030cm，以确保有足够高的测量精度。传声器的安装有两种方式。

第一种是将68个传声器绑在一根横杆上，如图3-18所示，横杆可以前后和上下移动。测试时，首先将横杆放置在一个位置进行测量，然后前后移动横杆到不同的位置测量，再上下移动横杆到不同位置再测量。经过多次移动横杆和多次测量后，得到整车空腔内的声压。

传声器的第二种安装方式是在整个车内按照2030cm的间距，在前后、横向、上下布满传声器，形成传声器阵列，如图3-19所示。一次测试就得到了整个声腔内的声压分布。与第一种安装方式相比，第二种方式测试时间短、速度快，但是需要的传声器数量多，成本高。

图3-18 安装在横杆上的 传声器

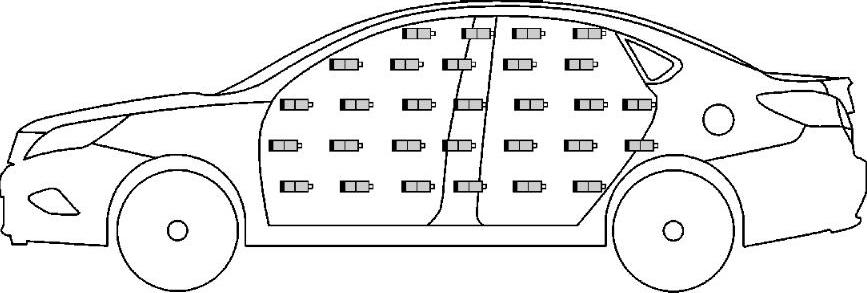
图3-19 车内传声器阵列

测试声腔模态的激励源通常采用体积声源，如图3-20所示，以便有足够的能量激起所需的声腔模态。另一种激励方式是使用高质量的低频扬声器。体积声源的位置不能放置在模态节点地方。在不能确定节点位置之前，可以尝试地将声源放置在不同的地方，然后通过检查传声器测量的响应与体积声源的激励之间的相关函数来确定合适的激励位置。

通过测量得到了响应声压和激励源之间的传递函数，便可以得到声腔模态和频率。图3-21为测量某车身的第一阶声腔模态，声压沿着车身的纵向变化，这与计算结果是一致的。

(www.xing528.com)

图3-20 体积声源

图3-21 测试的声腔模态

3.座椅对声腔模态的影响

图3-22是有座椅的声腔有限元模型。图3-23是有座椅的前五阶声腔模态，将之与图3-17中无座椅的声腔模态振型比较，可以看到它们对应的振型只有微小差别，但是振型形状基本一致，即第一阶和第二阶是纵向模态，第三阶是横向模态，第四阶是纵横交错的模态，第五阶是复合模态。

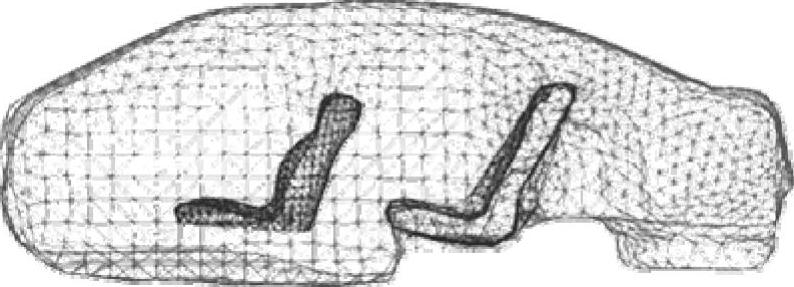
图3-22 有座椅的声腔有限元模型（见彩插）

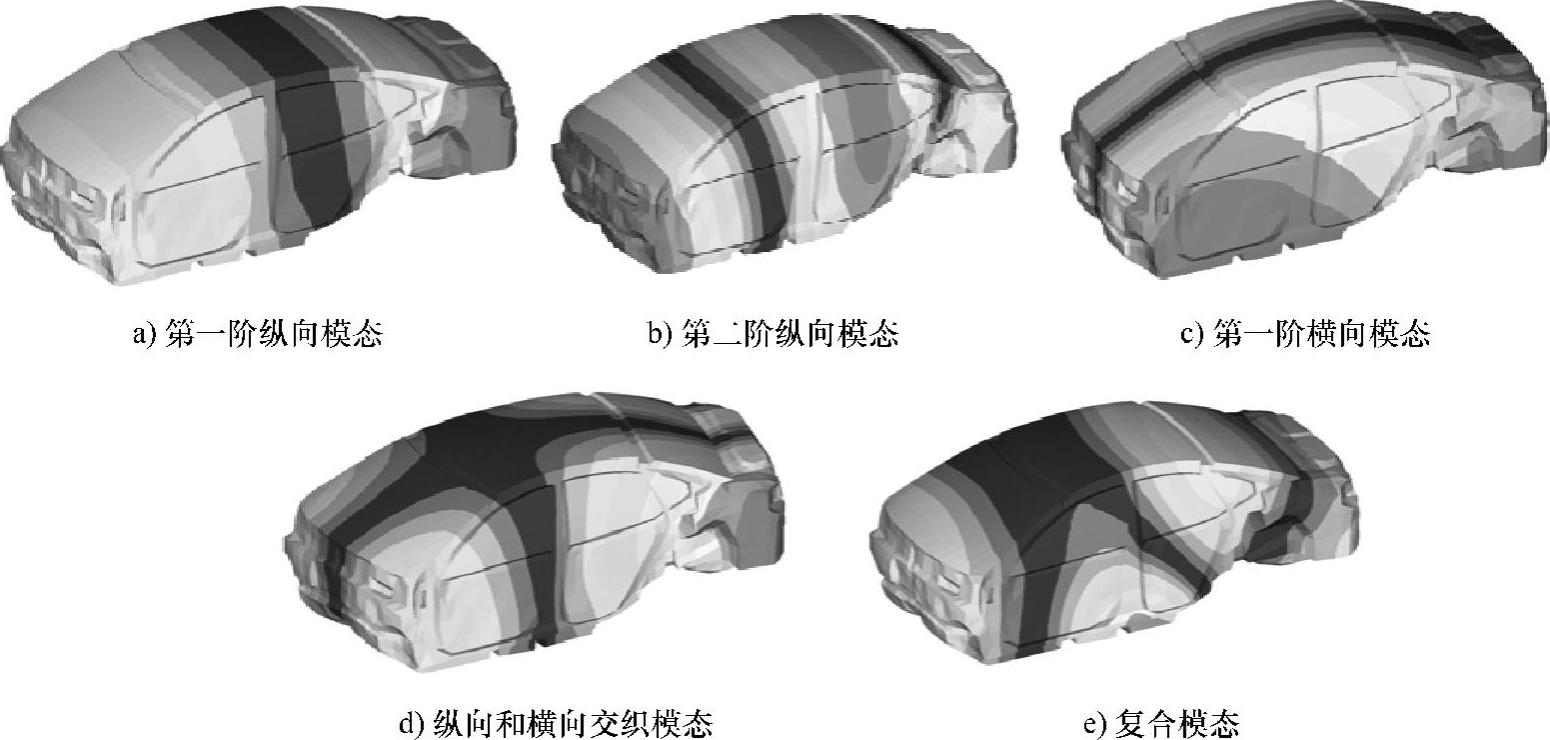
图3-23 有座椅的前五阶声腔模态（见彩插）

将无座椅和有座椅的声腔模态频率列入表3-8中，比较加入座椅后声腔模态频率的变化。加入座椅后，第一阶声腔模态频率从57Hz降低到50.1Hz，第二阶声腔模态频率从102.5Hz降低到96.2Hz，第三阶声腔模态频率从119.5Hz降低到118.4Hz，第四阶声腔模态频率从141.4Hz降低到139.8Hz，第五阶声腔模态频率从153.6Hz降低到150.8Hz。也就是说，座椅使车身的声腔模态频率变低，而且对低阶模态频率的影响高于高阶模态。

座垫和靠背由泡沫材料组成。这些泡沫材料里面充满着空气，形成了一个特殊的腔体。当泡沫腔体与车身的空气腔体耦合在一起时，它们共同组成的腔体模态频率就降低。因此，在分析声腔模态时，应该考虑座椅的影响。人如坐汽车内，声腔模态的频率会进一步降低。

表3-9给出了声腔模态常见的形式和频率范围。了解了声腔模态的振型和频率范围后，在分析车内轰鸣声时，可以将它们与车身板的结构模态对比，从而找出产生轰鸣声的板。

表3-8 没有座椅和有座椅的声腔模态频率

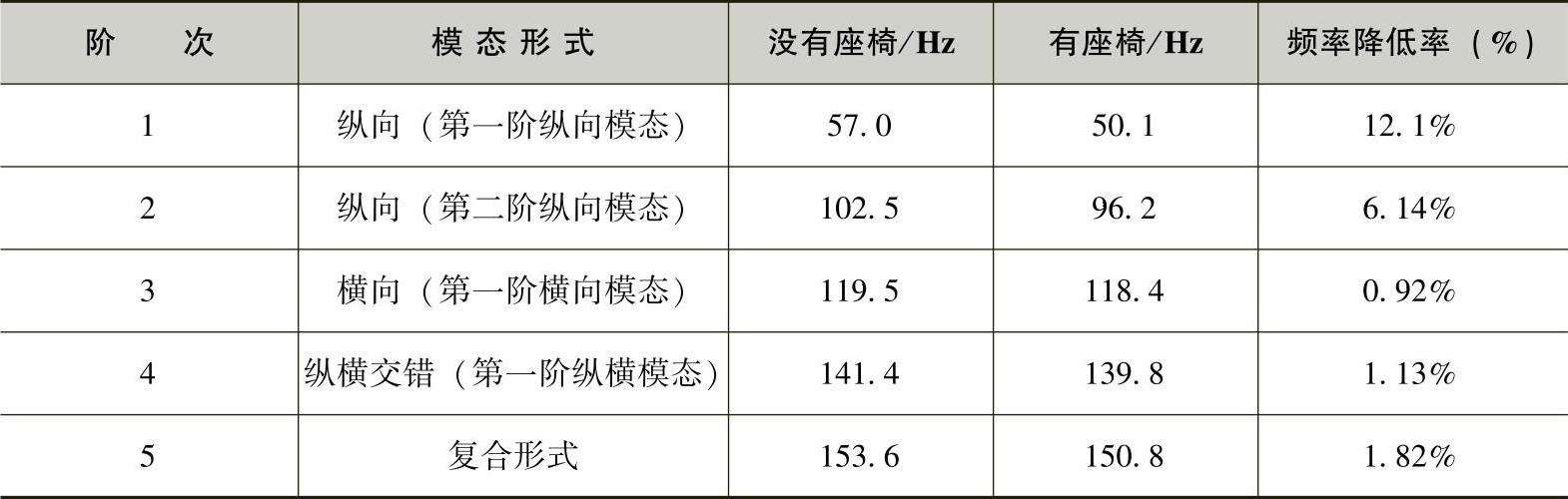
表3-9 声腔模态常见的形式和频率范围

由于大多数车内轰鸣声集中在30100Hz，因此分析声腔模态时，主要关心前三阶模态。纵向模态引起的轰鸣声是最常见的情况，因此在分析结构模态与声腔模态引起的轰鸣声问题时，需要重点分析车身上垂直于纵轴（x方向）的板结构。这些板的振动方向与声腔压力变化的方向是一致的，都沿着纵向。

当一辆车的尺寸确定后，其声腔模态的形式和频率就基本定了，因此要改变车身的声腔模态频率几乎是不可能的，但是可以通过一些调整来改变节点位置，使人耳尽可能接近节点位置。

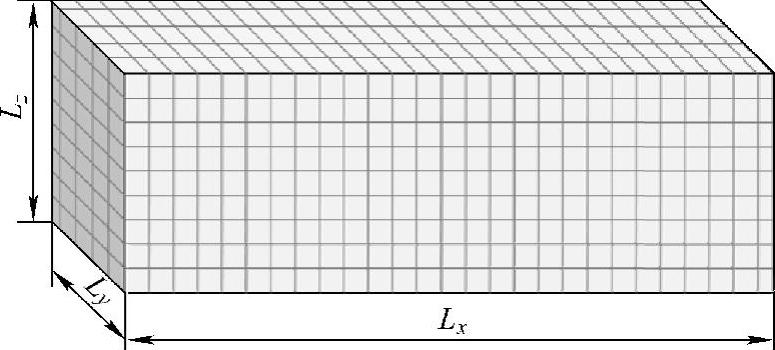
图3-24 长方体声腔

4.声腔模态频率的简单计算公式

声腔模态的有限元方法能给出其模态形式和频率。汽车开发过程中，当需要快速预估声腔模态频率时，可以将声腔简化成一个长方形的盒子（图3-24），从而预估出其模态频率，计算公式为

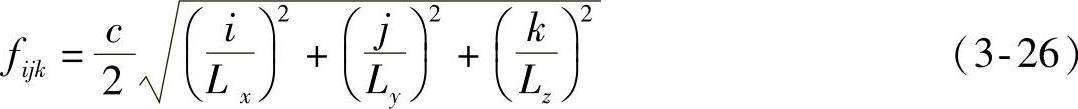
式中，c是声速；L_x、L_y和L_z分别是声腔在x、y和z三个方向的长度；i、j和k分别是x、y和z三个方向的模态阶数。

声腔模态振型可以用下面的简单公式来表示：

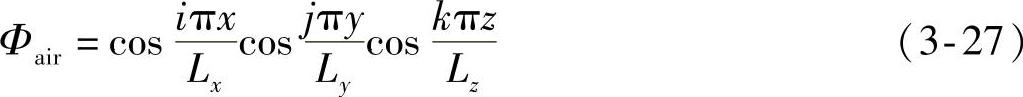
将图3-16的有限元模型进行简化，取三维方向最大尺寸，使之变成一个矩形，如图3-24所示。图3-16所示模型的三个方向最大尺寸分别为：L_x=3248mm、L_y= 1491mm，L_z=1282mm。建立这个矩形的有限元模型并计算出模态频率，然后与式（3-26）计算值及真实声腔有限元计算值比较，前三阶模态频率的比较见表3-10。

表3-10 用有限元方法和用公式计算的矩形声腔模态频率的比较（单位：Hz）

用简单公式与矩形有限元模型计算的值是一致的，但是与真实声腔模型计算的值有一定差距，其原因是公式计算或矩形模型与真实模型是不一样的。在一个方向（如x方向）上，矩形模型从一端到另一端的尺寸相同，而真实模型不一样，这样就使它们的计算值出现不同。用简单公式或矩形模型来计算，第二阶纵向模态频率是第一阶纵向模态频率的一倍，而真实模型不存在这种关系，原因是真实模型复杂而且并非完全对称。尽管有这种差距，但是用简单公式来计算车身声腔模态频率的方法还是有用，有三个原因：第一是它们的差别并不是太大；第二是计算结果的趋势是一致的；第三是简单计算可以快速地估算声腔模态频率，对快速进行工程问题的判断有帮助。