板结构声辐射分析及介绍

在研究板的声辐射之前，先来分析点声源的辐射。点声源（图3-12）是一个单极子声源，它对空中辐射的声压，p（r，t），表达为

式中，r是点声源到辐射点的距离；ρ₀是空气密度；ω是频率；Q是体积速度；k是波数。

jωρ₀ Q被称为“单极子声源强度”。

将式（3-6）中的一部分定义为自由空间格林（Green）函数，G（r，ω），表达为

将式（3-6）代入式（3-7），可以得到格林函数的另外一个表达式，为

从式（3-8）中可以解读格林函数的意义，它表示为辐射到远场的声压与体积声源之间的传递函数。这个意义对理解车身板的声辐射非常重要。

如结构的振动计算一样，声辐射的计算也只能针对简单结构和特殊的边界条件。与结构的振动计算相比，声辐射的计算更加复杂。目前，板的声辐射解析分析只是针对矩形板、圆形板这样的简单结构，而且板的四周用无限的障板包围，即将有限的矩形板或者圆形板（如活塞）放置在无限的障板之中。

本书以在无限大障板中的矩形板（图3-13）的声辐射来介绍板件声辐射的一些概念和问题，如辐射效率、声强等。矩形板的长宽分别是a和b。

矩形板可以分解成许多小块。每个小块可以看成是一个点声源，面积为δS。假设第n块板的法向速度为u_n，小块辐射的体积速度则为u_nδS。板振动产生声波向两边辐射。如果只考虑声音向单面辐射，则体积速度为

图3-12 点声源对空中声辐射

图3-13 无限大障板中的矩形板对空中声辐射

把式（3-9）代入式（3-6），矩形板中的一个点声源（x，y）对空中任意一点（x′，y′，z′）的辐射声压可以写成

式中，u_n（r_s）是板件表面的振动速度；r_s为板件振动表面位置（x，y）矢量，r为观察点位置（x′，y′，z′或r，θ，ϕ）对原点的矢量，R是r-r_s的模，即R=r-r_s。当观察点的距离远远大于矩形板的尺寸时，即R>>a，b，R≈r-xsinθ cosϕ-ysinθsinϕ。

板向单面辐射是所有“点”单元辐射的集合，根据Rayleigh公式，可得到板辐射空间的声压为

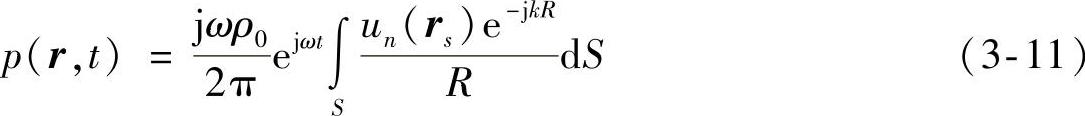
对式（3-3）微分，可以得到简支矩形板的法向速度分布，表达为

u_n（x，z）=jωA_ij sin（iπx/a）sin（jπz/a） sin(jπz/b)e^jwt（3-12）(www.xing528.com)

将式（3-12）代入式（3-11），得到空间任意一观察点（x′，y′，z′）的辐射声压为

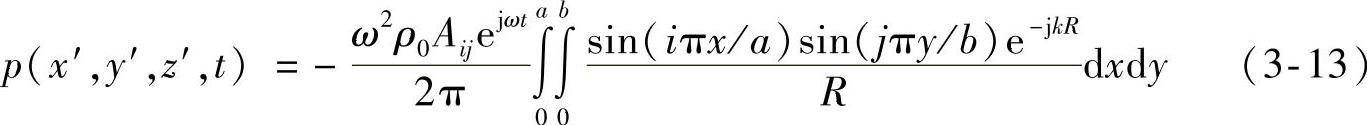
在远场，质点速度与声压的关系为

空中R位置的声强为

式中，∗表示共轭复数。

无限大障板中简支矩形板做简谐振动，在远场，R>>a，b，它的辐射声强可以表示为

式中，α=kasinθcosϕ；β=kbsinθsinϕ。

当i取奇数、j取偶数时，项取cos cos ；当i取偶数、j取奇数时，取cos sin ；当i取偶数、j取奇数时，取sin cos ；当i、j取偶数时，取sin sin 。当声波频率很低、波长很长（远大于板的尺寸）时，可得远场声强最大值为

模态辐射声功率可由远场声强对无限大障板一面的半球面积分得到，即

辐射效率定义为空中辐射的声能量与板的振动能量比值，表达为

式中 为板的均方振速。对于四边简支矩形板，其均方振速为

将式（3-18）和式（3-20）代入式（3-19），得四边简支矩形板模态辐射效率为

若声波频率很低，波长很长（大于板的尺寸），此时，α<<iπ，β<<jπ，并且当i、j取奇数时，辐射效率为