汽车车身噪声于振动控制：简支结构振动

板结构的振动非常复杂，只有对一些简单的板结构，如简支的矩形板，才能得到解析解。车身板与纵梁和横梁相连接，由于梁的刚度远远大于板的刚度，板在与梁连接处的变形远小于板其他部位的变形，所以此处的变形接近于零。在连接处的挠度和弯矩的边界条件比较难确定，如果挠度和转角接近于零而弯矩不接近于零，那么可以近似为固定边界条件；反之，如果挠度和弯矩接近于零而转角不接近于零，则近似为简支边界条件。车身板的实际边界条件介于简支和固定之间，但是更接近于简支边界。下面就以简支板来说明板的振动问题。

图3-10 矩形板

薄板中的振动传播主要呈现弯曲波的形式，下面来分析板的振动特征。图3-10是一个矩形板，长度为a，宽度为b，厚度为h。

薄板振动方程为

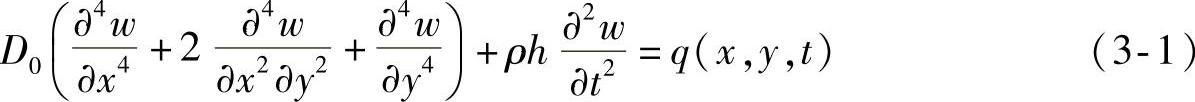
式中，ρ为密度；w为z方向的位移；q为表面载荷；D₀为薄板弯曲刚度，表示为

式中，μ是波松比；E是杨氏模量。

对于四边简支的矩形板，其振型函数为

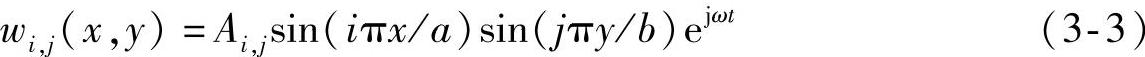
式中，A_i，j为振型幅值；i、j分别是沿着x和y方向的模态数，i，j=1，2，3，…。

这个振型函数满足四边简支的边界条件，即

(www.xing528.com)

将振型函数和边界条件代入方程（3-1），可以解得系统的固有频率，为

车身板由许多小块板组成，梁可以看成是板的边界。这些小板的边长通常为300400mm，厚度在1mm左右。下面就以一个边长为300mm和400mm、厚度为1mm的矩形简支板为例，来说明它的振型和频率。表3-5列出了板的几何尺寸和物理参数。板的振动分析可以用解析方法，也可以用数字方法（如有限元）。表3-6列出了根据式（3-5）计算和用有限元分析得到了该板的前10阶频率。有限元分析的结果比理论值低，但是前几阶模态频率非常接近。随着分析频率的增加，两种方法计算值之间的误差加大，这是由于有限元网格的划分使得板的刚度降低所致。

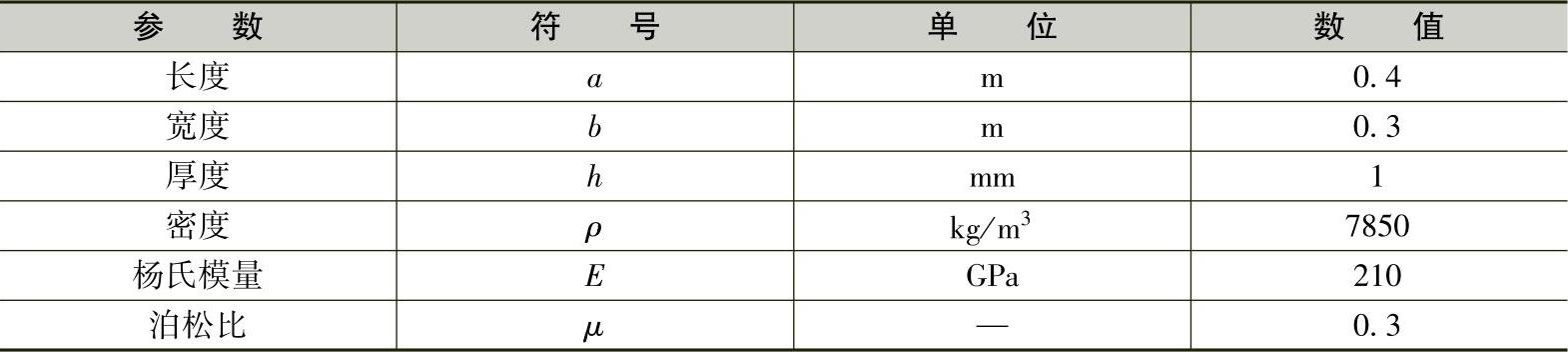
表3-5 矩形板的几何尺寸和物理参数

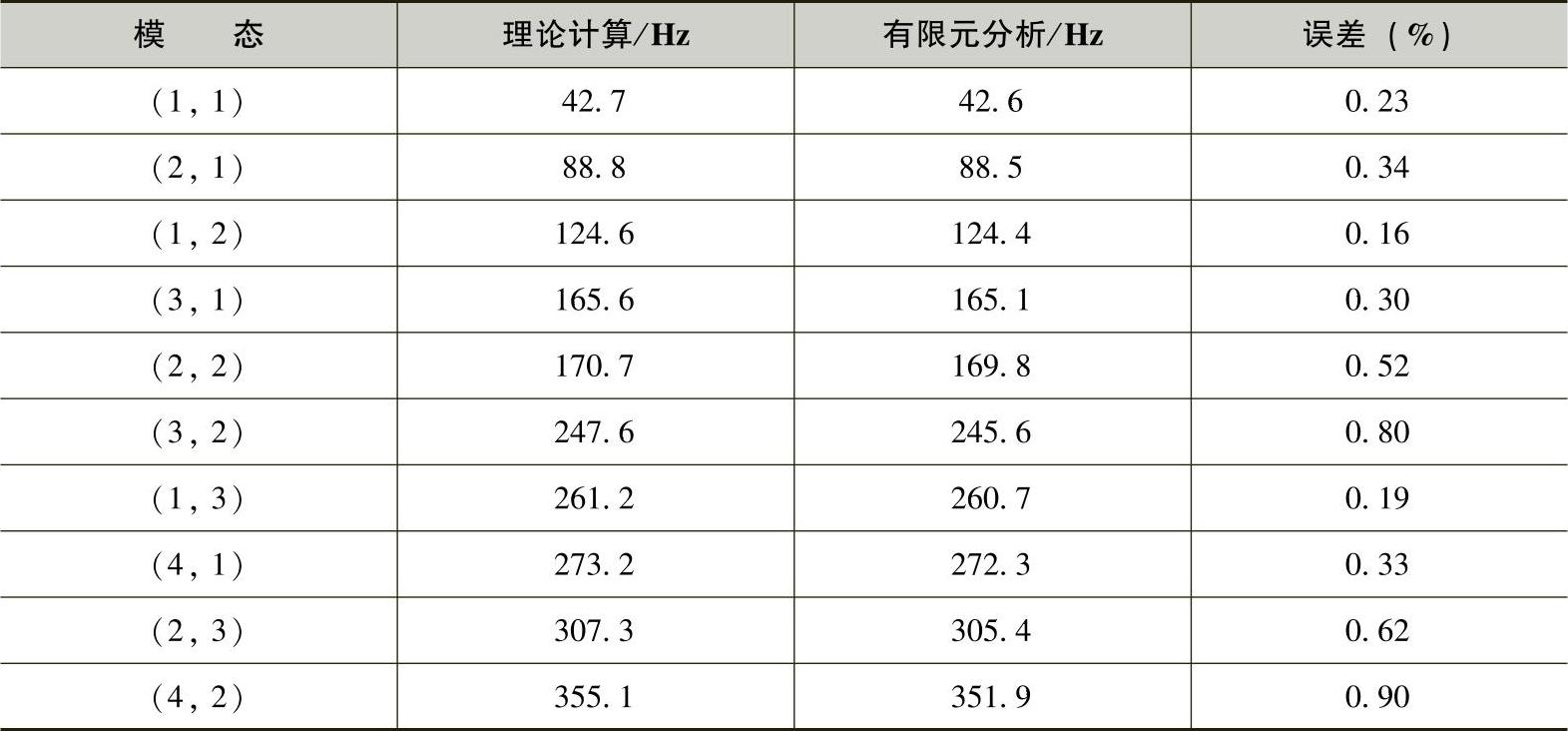
表3-6 矩形板的理论计算和有限元分析频率

图3-11为用有限元计算的矩形简支板的前10阶振型。振型呈空间分布，每一阶振型用两个数字来表达，如（3，2）阶振型。括号中的第一个“3”代表x方向的振型，第二个“2”代表y方向的振型。

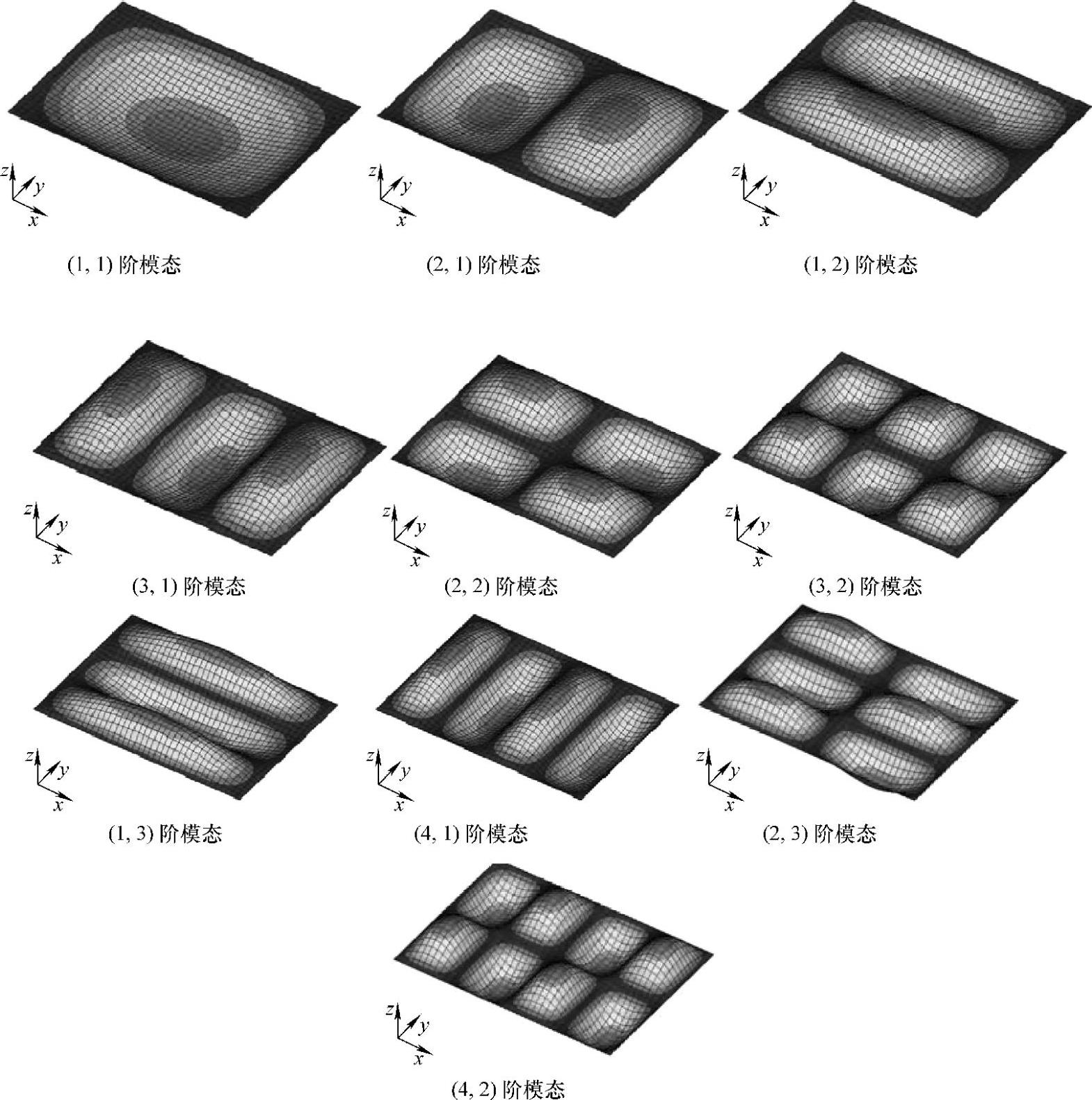
图3-11 矩形薄板的前10阶模态振型（见彩插）

这个矩形板最基本的振型是（1，1）阶振型，它对应的频率为42.6Hz。它是一个以中心为对称点、在x和y方向对称、上下运动的振型。振型最大幅值出现在中间。（2，1）阶的频率是88.5Hz，振型是以y轴的中线为对称轴线，轴线上的振型位移始终是0，即它是一条节线。在轴线的左右两边，板的振型分别做向上和向下运动，相位相差180°。（1，2）阶的频率是124.4Hz，其振型与（2，1）阶类似，只是对称轴线沿着x轴。随着阶次的增加，振型变得越来越复杂。

了解板的振型有助于声辐射的控制。比如，（1，1）阶振型类似于一个单自由度质点振动，可以将它视为一个单极子声源。（2，1）阶振型像两个相反运动的物体，可以把它看成相位相差180°的两个声源，即双极子声源，它们在远场产生的声音相互抵消。从远场声辐射的角度来看，（1，1）阶的振动模态必须控制，而（2，1）阶的振动模态可以不控制。

对于简支矩形板这样的简单规则结构，可以用解析方法得到模态频率和振型，但是对于复杂的结构，用解析法来求解是不可能的，只能采用数字方法，如有限元。对于车身这样复杂的结构，求解结构振动特征和响应几乎都是用有限元方法。在得到了车身结构的振型后，就可以分析每阶振型可能带来的声辐射，从而从结构上来控制板的振动，如加筋、加质量、加阻尼，等等。