汽车车身模态计算成果-阻尼忽略验证

车身是一个非常复杂的弹性连续体，通过数字解析分析来得到车身模态是不可能的。目前，最常用的方法是有限元法。有限元法是将车身这样的弹性连续体简化成有限个自由度的离散体，通过建立有限个自由度离散方程组来求解系统的模态参数。

车身自身的阻尼很小，而且对模态频率和模态振型的贡献很小，因此在用有限元进行模态计算时，通常将阻尼忽略。不过，在计算响应和频响函数时，需要考虑阻尼的影响。式（2-33）可以简化为

建立车身有限元模型是分析的第一步。车身有限元模型的建立是以CAD三维数据为基础，进行网格划分；然后，确定车身的边界条件为自由边界，即不施加任何约束；最后，采用合适的方法进行计算，得到结果。有限元的模态计算方法有很多，如子空间法、兰索斯（Lanczos）法、模态浓缩法等。

车身的主要模态频率在100Hz以内，但是与车身相连的系统的模态频率或者激励频率会超过100Hz，同时考虑到局部模态的频率范围，因此，通常将分析频率设为250Hz；当频率再高时，计算的工作量会大大增加，同时精确度下降；当频率高到一定时，系统的模态难以区分清楚，需要用统计方法来计算。

图2-51是用有限元法计算出的某个车身的第一阶弯曲模态和第一阶扭转模态。

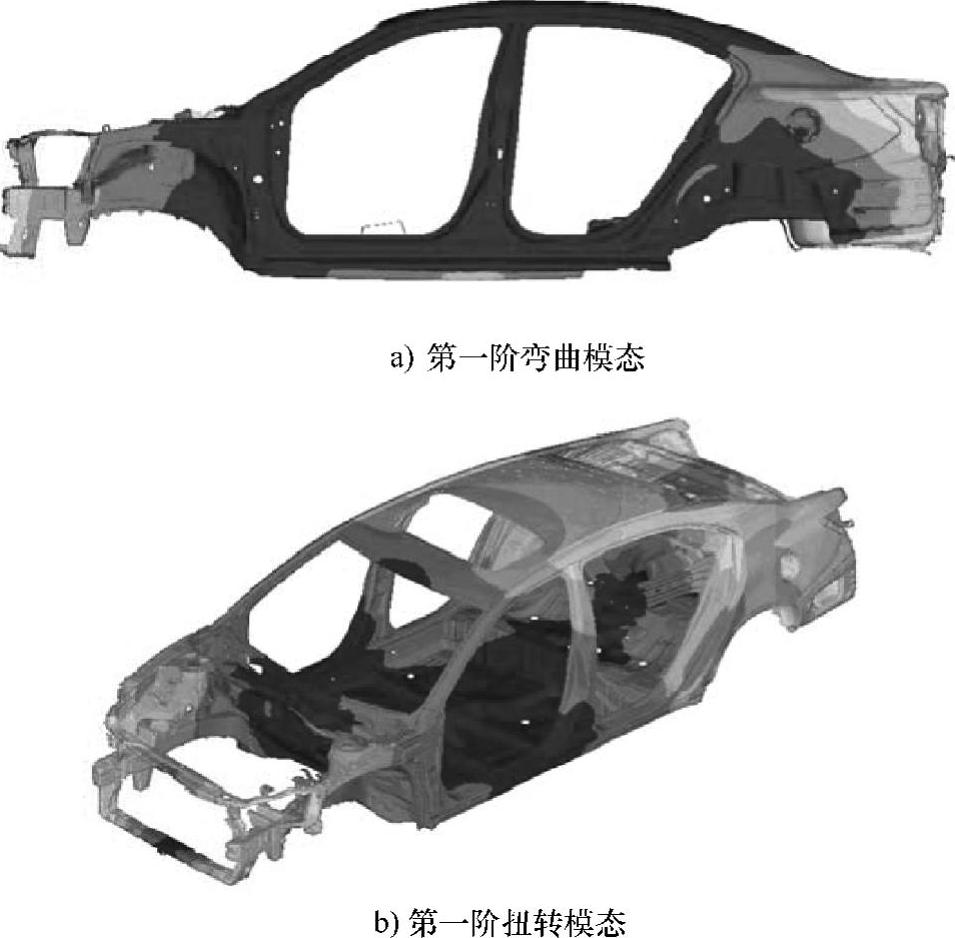
图2-51 有限元法计算的白车身的第一阶弯曲模态和第一阶扭转模态（见彩插）

为了验证有限元法计算的模态的准确性，可以将计算模态值与测试模态值进行比较，以便对计算模态进行修正。这种比较从固有频率、振型的视角、模态置信因子、频响函数等几个方面进行。(www.xing528.com)

首先是固有频率比较。将计算的和测试的固有频率列在一张表上，比较相关的频率。对车身模态来说，计算频率和测试频率之间的百分比误差在3%之内，就表明是同一模态频率。

第二是视角比较。以动画的形式显示出测试模态振型和计算模态振型，观察它们振型的形状和运动形式，来确定两者之间的关联性。

第三是计算模态置信因子。由于计算模型的自由度远远大于试验模型自由度，因此需要将计算模型进行模型减缩，使它与试验模型自由度相同。模型减缩的方法有很多，但是必须保证减缩后的模态与原始有限元模态特征一致。

将测试模态向量ϕ_t和计算模态向量ϕ_c进行比较，定义模态置信因子（MAC）为

当ϕ_t和ϕ_c为同一模态时，MAC≈1；当ϕ_t和ϕ_c为不同模态时，MAC≈0。MAC在0～1之间。MAC值越大，表明两个模态越相关。通常相关模态的MAC值大于0.8。可以将所有试验模态和计算模态的MAC值计算出来，构成一个MAC（i，j）矩阵。如果试验模态和计算模态的一致性好，那么MAC对角线上的值都接近于1，而非对角线上的值接近于0。

第四是频响函数比较。在计算频响函数时，必须考虑阻尼。将计算的和测试的频响函数绘制在一张图上，比较它们的形状、频率和峰值等方面的差异，以判断计算与测试值的可信度。