【摘要】：减振器压缩阀开阀前油路，如图9-7所示。根据对速度特性的要求，压缩阀片所承受的压力应满足式，即利用压缩阀常通节流孔压力与流量关系及油液连续性定理，可得压缩阀常通节流孔的面积为式即为压缩阀常通节流孔面积的数学模型。同理可知，设计速度点不同，则压缩阀常通节流孔面积设计值不同，即压缩常通节流孔设计面积具有非线性。
减振器压缩阀开阀前油路，如图9-7所示。
图9-7中，Qt为减振器在某一时刻的总流量，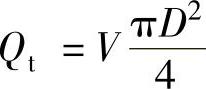
，同时也等于流向到腔流量Qh与流到下腔的流量Qg之和，即Qt=Qh+Qg。
设在压缩行程初次开阀前的任意速度Viy∈（0，Vk1y]点，流通阀压力为pLi，根据流通阀的速度、流量和节流压力以及阀片变形量之间的关系，可得流通阀的压力方程为
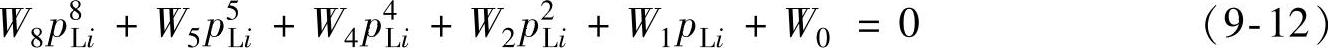
式中，W8=b2D；W5=2bcD；W4=2abD+bC；W2=c2D；W1=2acD+cC-1；W0=aC+a2D。其中，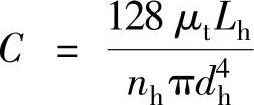
，
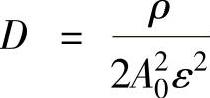，a=ShViy，b=-kQl，c=-kQH，kQH=
，
。
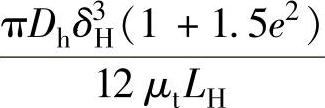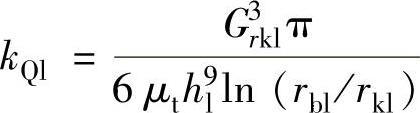因此，利用流通阀压力方程式（9-12），可以得到压缩行程开阀前流通阀的节流压力pLi。
在压缩行程初次开阀前的任意速度Viy时，压缩阀座孔的节流压力可表示为
(www.xing528.com)
式中，Sg为活塞杆面积，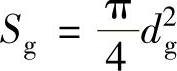
；Ahy为压缩阀座孔的面积，
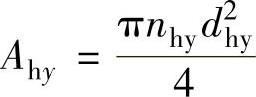，其中，dhy为压缩阀座孔的直径；nhy为压缩阀座孔的个数。
根据对速度特性的要求，压缩阀片所承受的压力应满足式（9-14），即
利用压缩阀常通节流孔压力与流量关系及油液连续性定理，可得压缩阀常通节流孔的面积为
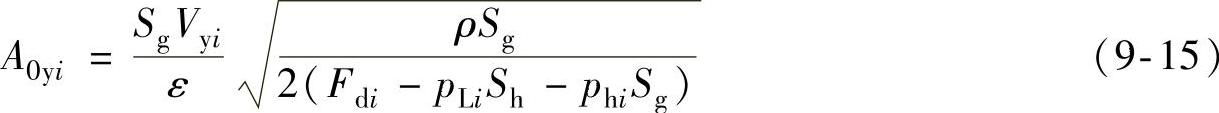
式（9-15）即为压缩阀常通节流孔面积的数学模型。同理可知，设计速度点不同，则压缩阀常通节流孔面积设计值不同，即压缩常通节流孔设计面积具有非线性。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
