汽车减振器设计与特性仿真：环形集中力下的阀片应力数学模型

根据弹性力学原理，阀片在半径r位置上、下表面（z=±h/2，z为阀片轴向位置坐标）处的应力最大。由应力与内力之间的关系，可得阀片上、下表面上的径向应力和周向应力分别为

将式（8-54）和式（8-55）分别代入式（8-56）和式（8-57），可得

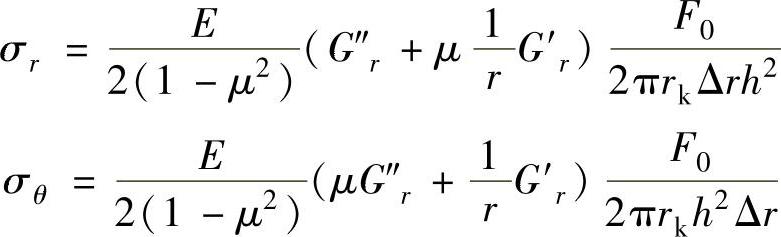
令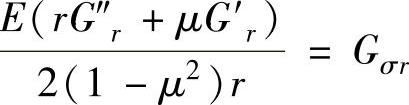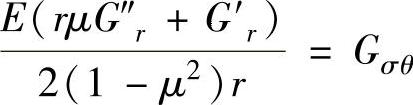，，则上两式可表示为

式中，Gσr为阀片径向应力系数；Gσθ为周向应力系数，单位为m²或mm²。二者均为阀片应力“长城”系数。

根据第四强度理论，阀片所受的复合应力为

(www.xing528.com)

将式（8-58）和式（8-59）代入式（8-60），可得

式中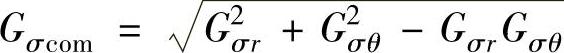，为节流阀片在非均布压力下的复合应力系数，即阀片复合应力“长城”系数。

阀片在弹簧预紧力下的应力“长城”系数，不仅与阀片的结构、弹性模量和泊松比有关，还与弹簧半径大小有关。例如，某环形节流阀片的内半径r_a=5.0mm，外半径r_b=8.5mm，弹性模量E=200GPa，泊松比μ=0.3，在半径r_k=7.0mm的弹簧作用下，阀片在任意半径r处的各向应力“长城”系数，如图8-22所示。

由图8-22可知，对于给定弹簧半径r_k的情况下，可求得环形阀片在半径r处的径向应力、周向应力和复合应力“长城”系数，利用式（8-58）、式（8-59）和式（8-60），便可分别解析计算节流阀片任意半径r处的径向、周向和复合应力。

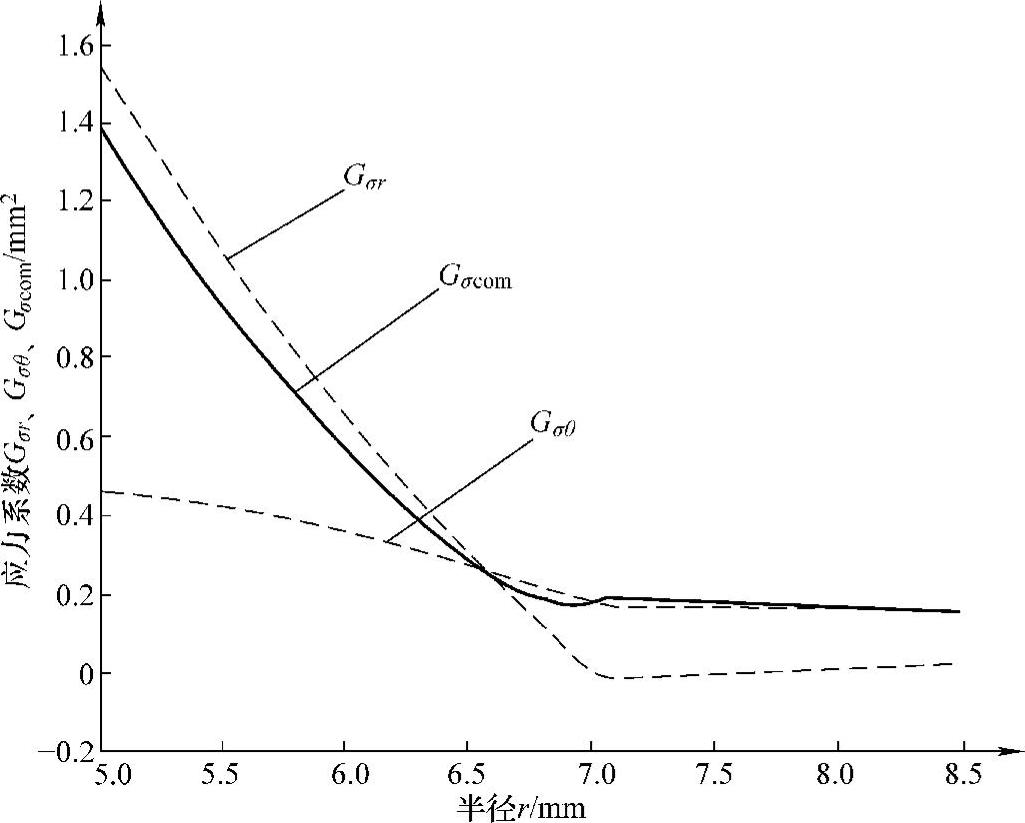
图8-22 阀片在弹簧力作用下的应力系数