设计仿真：汽车减振器阀片压力引发的非均布变形

1.阀片变形曲面方程

由图8-9可知，阀片所受的线性非均布压力可表示为

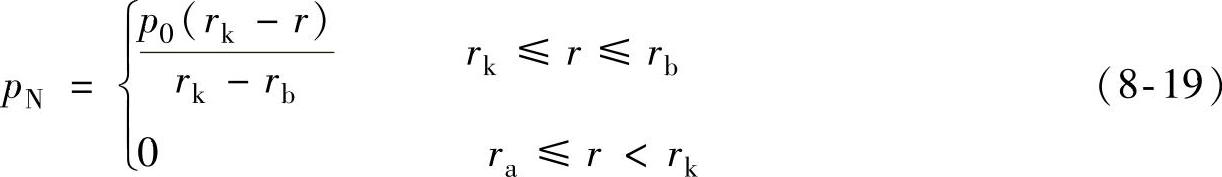
由于阀片的结构和载荷都绕z轴对称，所以根据弹性力学可得节流阀片线性非均布压力作用下的变形曲面微分方程可表示为

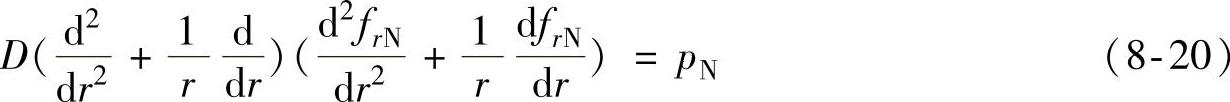
式中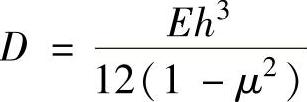，；E是阀片材料弹性模量；μ是阀片材料泊松比。

2.曲面方程的解

将式（8-19）代入式（8-20），可得上述阀片在非均布载荷作用下的变形曲面微分方程[式（8-20）]的通解为

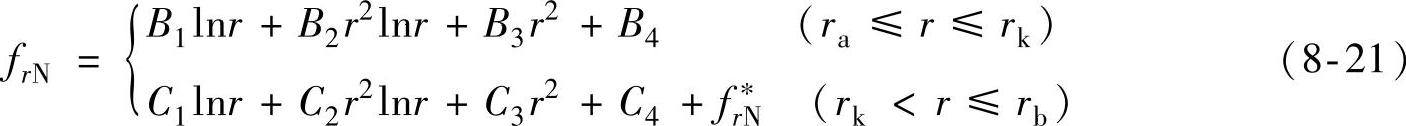
式中，f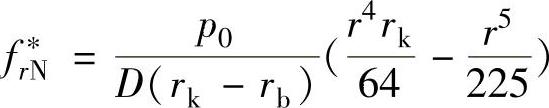；B₁、B₂、B₃、B₄、C₁、C₂、C₃和C₄为8个常数，可由节流阀片在内圆和外圆处的边界条件，以及半径r_k处的连续性条件所确定。

1）内圆处的变形量等于零，即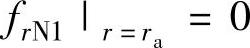，根据阀片变形曲面的通解（8-21）可得

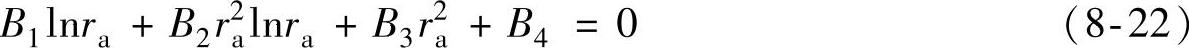
2）内圆处的变形斜率等于零，即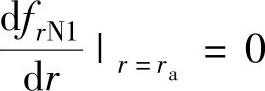，可得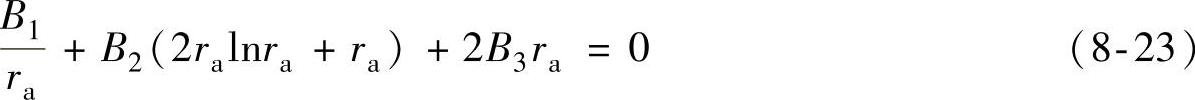

3）外圆处的力矩等于零，即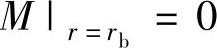，可得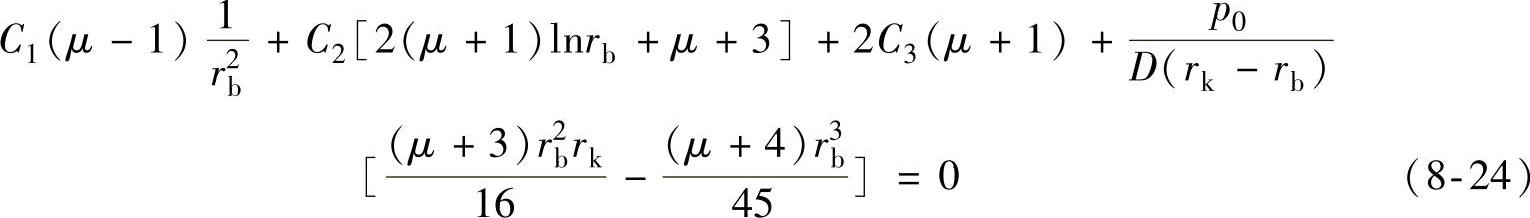

4）外圆处的剪切力等于零，即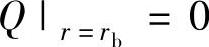，则可得

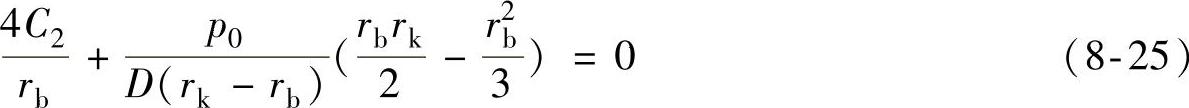(https://www.xing528.com)

5）阀片半径r_k处的变形连续，即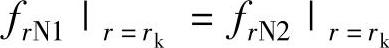，可得

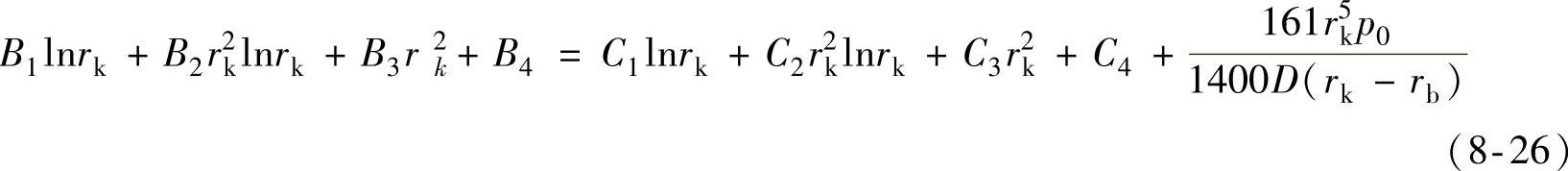
6）阀片半径r_k处的变形斜率相等，即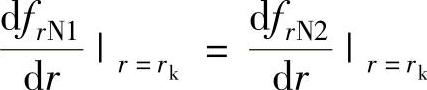，因此可得

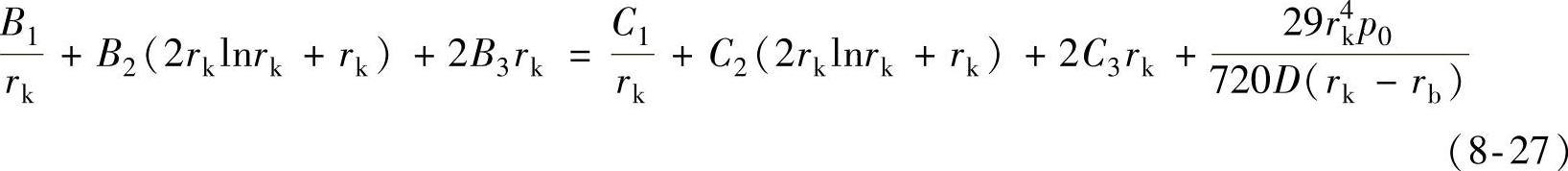
7）阀片半径r_k处的弯矩相等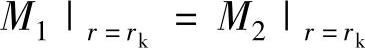，，可得

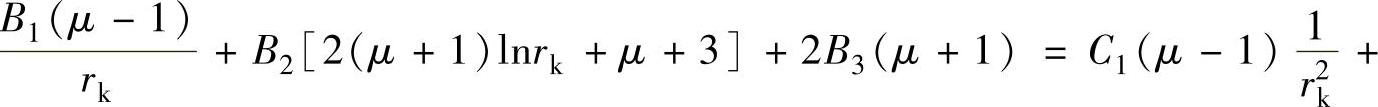
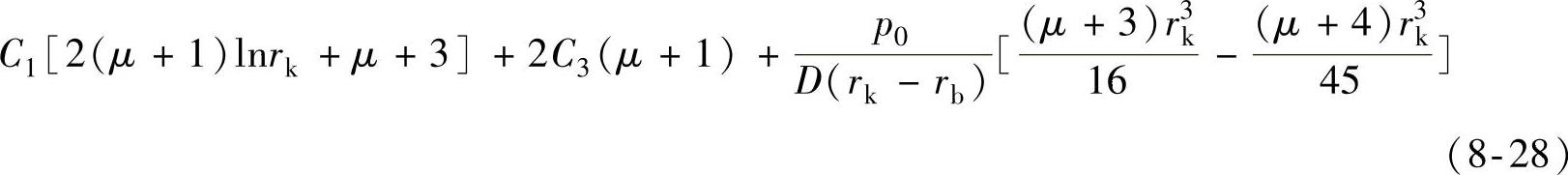
8）阀片半径r_k处的剪切力相等，即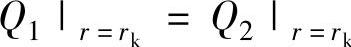，因此可得

通过联立式（8-22）～式（8-29），可求得环形节流阀片在线性非均布载荷作用下的弯曲变形微分方程通解的8个常数，即B₁、B₂、B₃、B₄、C₁、C₂、C₃和C₄，从而得到在线性非均布载荷下阀片弯曲变形微分方程通解表达式。

3.阀片变形解析计算式

根据上述边界条件和连续性条件，可得8个常数，将它们代入阀片变形曲面微分方程的通解[式（8-21）]，便可得到在线性非均布压力下，节流阀片在任意半径r处的变形解析式。由分析可知，阀片变形解的各项都含有一个公因子p₀/h³，对式（8-21）提取公因子p₀/h³，将剩余项归结为一个常数G_rN，即阀片在半径r位置处的变形系数，则阀片在半径r处的变形量可表达为

式中，G_rN即为阀片在线性非均布压力作用下，在半径r处的变形系数，即阀片变形“长城”系数，它不仅与阀片的结构、弹性模型、泊松比、半径位置有关，还与线性非均布载荷的加载位置有关。