汽车减振器设计与特性仿真：解析阀片变形曲面微分方程

汽车减振器节流阀片为圆环形弹性阀片，内半径r_a是固定约束，外半径r_b是自由约束，节流阀片在载荷p的作用下将产生变形。根据阀片的结构和受力特点，所建立的阀片力学模型如图8-1所示。

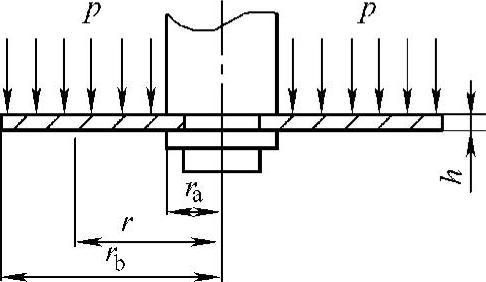
图8-1 节流阀片力学模型

节流阀片的结构和受力均是对称的，因此，可以节流阀片圆心为极点建立极坐标系。边界绕z轴对称，这样载荷和变形量只是半径r的函数。由于减振器开阀压力比较小，节流阀片大多时间处于小挠度变形状态，根据弹性力学原理，可建立节流阀片变形曲面微分方程为

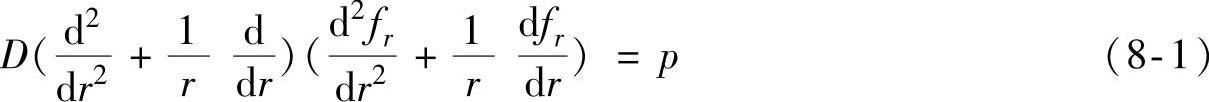
式中，常数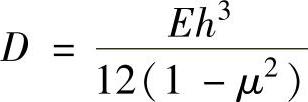；r为极半径，r∈[r_a，r_b]；f_r为阀片在半径r处的变形量，它是半径r的函数；h为阀片厚度；E为阀片弹性模量；μ为阀片材料泊松比。

对于厚度为h、弹性模量为E、泊松比为μ的给定阀片，D为常数。因此，微分方程（8-1）的通解可表示为

f_r=C₁lnr+C₂r²lnr+C₃r²+C₄+f_r^* （8-2）式中，f_r*为方程特解，C₁、C₂、C₃和C₄为方程解的常数，由阀片边界条件决定。

由于微分方程中的D和p均与半径r无关，因此设微分方程特解为f_r*=Br⁴，将其代入常微分方程，得(www.xing528.com)

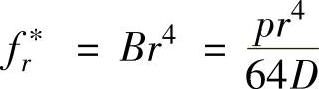
因此有

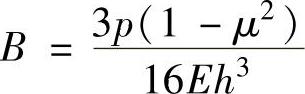
阀片内圆是固定约束，外圆是自由约束，环形阀片边界条件可表示为内圆：f_r|_r=r_a=0；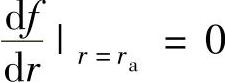

外圆：；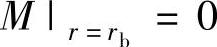

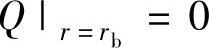
利用上述阀片的4个边界条件，可确定方程解中4个待定常数C₁、C₂、C₃和C₄。将所求得微分方程解的常数C₁、C₂、C₃和C₄代入阀片变形微分方程的通解，便可以得到节流阀片在半径r处的变形解析表达式，即

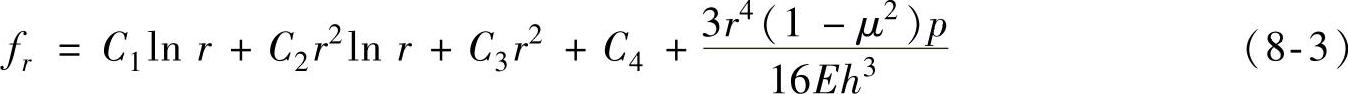
式（8-3）即节流阀片的变形曲面方程。利用此方程可以求得在给定压力下，阀片在任意位置半径r∈[r_a，r_b]处的变形量。