液体流经缝隙的流量模拟

在液压元件中，合理的间隙是零件间正常相对运动所必需的。间隙对液压元件的性能影响极大。讨论液流在间隙中的流动特性，对液压元件的设计、制造、性能分析以及计算泄漏量等都具有实际意义。

液压装置的各零件之间，特别是有相对运动的各零件之间，一般都存在缝隙（或称间隙）。油液流过缝隙就会产生泄漏，这就是缝隙流量。由于缝隙通道狭窄，液流受壁面的影响较大，流速较低，因此缝隙液流的流态均为层流。

通常来讲，缝隙流动有三种状况，一种是由缝隙两端压差造成的流动，称为压差流动；另一种是形成缝隙的两壁面作相对运动所造成的流动，称为剪切流动；还有一种是这两种流动的组合，即在压差和剪切联合作用下的流动。下面讨论在压差作用下的流量计算。

1.流经平面间隙的流量计算

图6-7所示为平行平板缝隙间的流动情况。设缝隙高度为δ，宽度为b，长度为l（一般l＞＞δ和b＞＞δ），设缝隙两端的压力分别为p₁和p₂，其压差Δp=p₁-p₂。假定上平板向右运动的速度为u₀，液体自左向右运动，从缝隙中取出一微小的单元，其左右两端面所受的压力分别为p和p+Δp，上下两侧面所受的摩擦切应力分别为τ和τ+dτ，方向如图6-7所示。

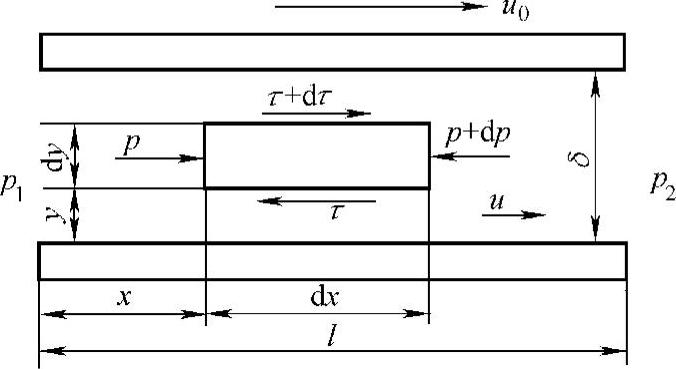
图6-7 平行板缝隙流量计算简图

恒定流动时微单元在水平方向上的受力平衡方程为

pbdy+（τ+dτ）bdx=（p+dp）bdy+τbdx

（6-51）

整理后得

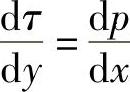
将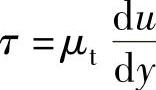代入可得

对式（6-52）积分两次得

式中，C₁、C₂都是积分常数。

当两平行平板的相对速度为u₀时，利用边界条件，即y=0、u=0和y=δ、u=u₀，代入式（6-53）可得

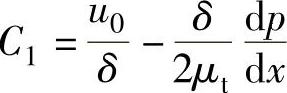
C₂=0

另外，液体作层流时压力只是距离（长度）的线性函数，即

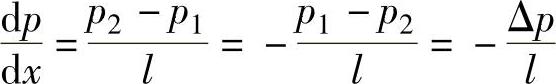
把这些关系式代入式（6-53）并考虑到运动平板有可能反向运动，可得

由此可求出液体在平行平板缝隙中的流量为

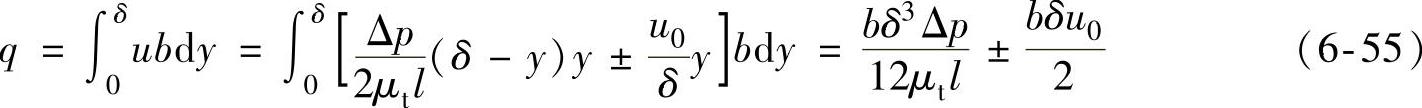
对于式（6-55）中“±”号的确定方法为：当动平板移动的方向和压差方向相同时，取“+”号；方向相反时，取“-”号。

当平行平板间没有相对运动时（u₀=0），流量为

当平行平板两端没有压差时（Δp=0），流量为

如果将通过缝隙中的流量理解为液压元件缝隙中的泄漏量，则可以看到，通过缝隙的流量与缝隙值的三次方成正比，这说明液压元件内缝隙的大小对其泄漏量的影响是很大的。此外，这些泄漏所造成的功率损失可写为

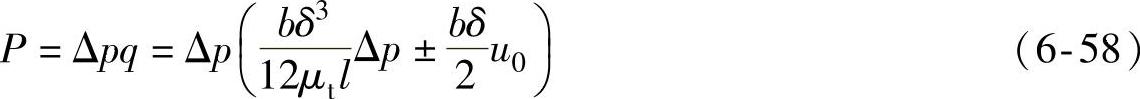
由此可得出结论：缝隙δ越小，泄漏功率损失也越小，但是并不是δ越小越好。δ的减小会使液压元件中的摩擦功率损失增大，缝隙δ有一个使这两种功率损失之和达到最小的最佳值。

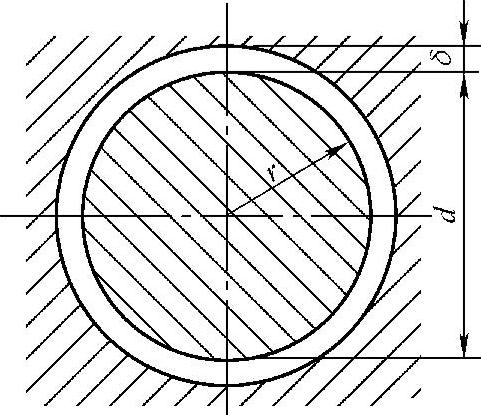
图6-8 环形缝隙(www.xing528.com)

2.同心环状缝隙的流量计算

在液压缸的活塞和缸筒之间，液压阀的阀芯和阀套之间，都存在着圆环缝隙。图6-8所示为同心环状间隙，圆柱直径为d，环形缝隙大小为δ，缝隙长度为l。

当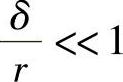（相当于液压元件配合间隙的情况）时，可将环形缝隙沿圆周方向展开，相当于一个平行平板缝隙。因此只要将b=πd代入式（6-55），就可得出内外表面之间有相对运动的同心环形缝隙流量公式，即

当相对运动速度u₀=0时，有

式（6-60）即内外表面之间无相对运动的同心圆环缝隙的流量公式。

3.偏心环状缝隙的流量计算

液压元件在实际工作过程中，圆柱体与孔的配合很难保持同心，往往带有一定偏心距，如活塞与液压缸不同心时就形成了偏心环状缝隙，如图6-9所示。

通过此偏心圆形缝隙的流量为

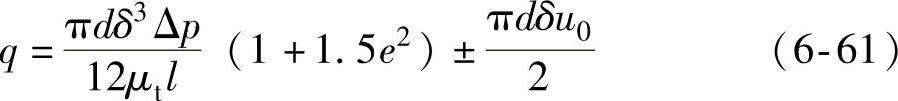
式中，δ为内外圆同心时的缝隙值；e为相对偏心率，。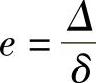

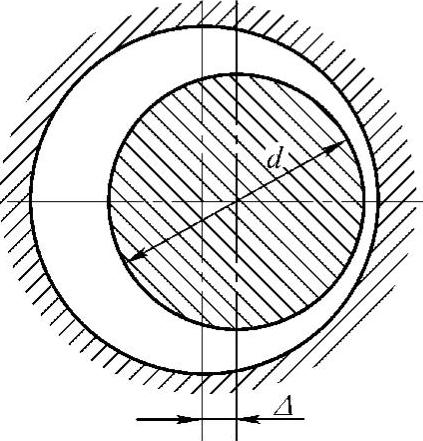
图6-9 偏心环形缝隙

当内外圆表面没有相对运动时，即u₀=0，其流量公式为

从式（6-62）可知，通过同心圆环形缝隙的流量公式是偏心环形缝隙流量公式在ε=0时的特例。当完全偏心时，即e=δ和e=1时，有

可见，完全偏心时的流量是同心时的2.5倍，在实用中可估计约为2倍。为了减小偏心环状缝隙产生的泄漏，在液压元件的设计制造和装配中应采取适当措施，如在阀芯上加工一些压力平衡槽以达到阀芯和阀套同心配合的目的，从而保证较高的配合同轴度。

4.圆环平面缝隙的流量计算

图6-10所示为一种在静压支承中（如轴向柱塞泵滑履中）的平面缝隙流动，液体自圆环中心向外辐射流出。

根据式（6-54），令u₀=0，则可得在半径为r且距离下平面为z处的径向速度u_r为

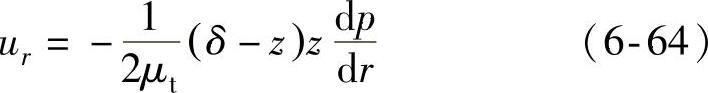
流过的流量为

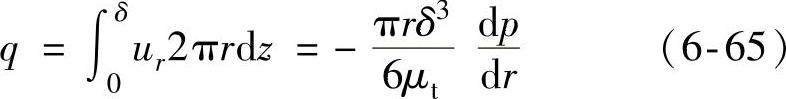
即

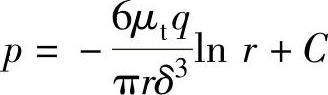
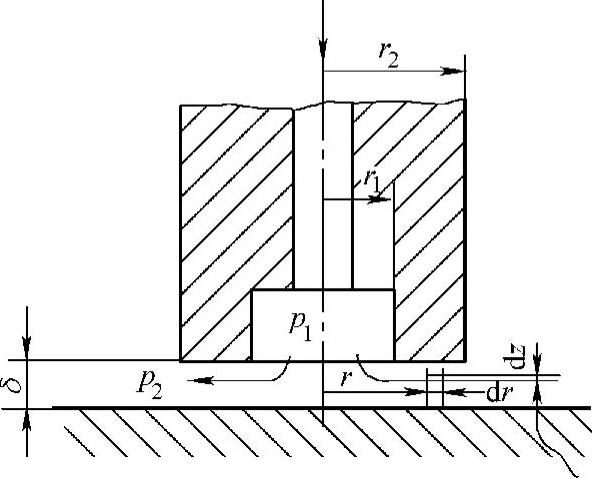
图6-10 圆环平面缝隙间的液流

当r=r₂时，p=p₂，求出C，代入得

又当r=r₁时，p=p₁，所以可得

对锥阀来说，如阀座的长度较长而阀芯移动量很小，使在锥阀缝隙中的液流呈现层流时，就可设想将它展开变成圆缺的环形平面缝隙液流，利用式（6-68），将式中的π代之以πsinϕ，以得出流经锥阀缝隙的流量。