汽车减振器设计与振动评价

车辆振动性能的评价指标，包括以下三个方面的内容：

1）车身振动强度K，反映舒适性。

2）车轮动载F_d，反映安全性。

3）悬架动挠度Δz_d，间接反映舒适性。

一般通过选取适当的加权因数，来获得总的评价指标，即

式中，F_d为车轮载荷变化（即动载）的有效值，代表行驶安全性的尺度；K为车身振动强度；w_F和w_K分别为车轮动载和车身振动强度指标的加权因数。

对于赛车，w_F大而w_K小；对于轿车，通过在行驶安全性和舒适性之间的协调选取w_F和w_K。加权因数确定后，就可以对悬架的弹簧和减振器进行优化设计和布置。

1.车轮动载

车轮载荷即车辆法向力F_z，简称“轮荷”，可作为车辆振动的评价指标，它涉及行驶安全性和道路应力。F_z是由静态垂直载荷F_zs和动态垂直载荷F_d两部分组成，如图3-16所示。

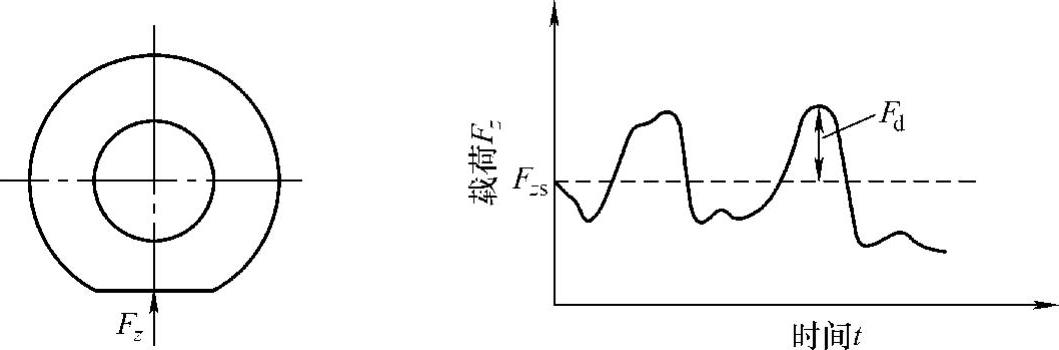
图3-16 静态载荷F_zs与动态载荷F_d的说明图

由图3-16可知，车轮载荷F_z等于静态垂直载荷F_zs与动态垂直载荷F_d之和，即

F_z（t）=F_zs+F_d（t） （3-79）车轮载荷F_z的方差σ²_Fz为

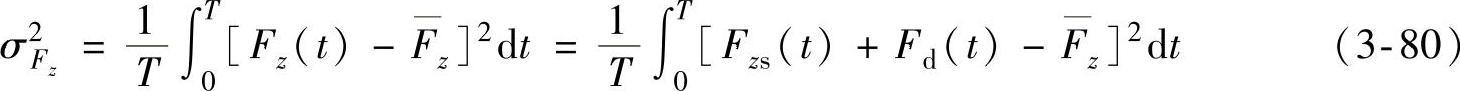
式中，F_z为车轮平均载荷。因为，车轮载荷的平均值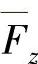一般应等于静态垂直载荷F_zs，即

所以按照功率谱密度的定义，车轮动载的功率谱密度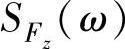可表示为

曾经用响应的谱密度计算其有效值，即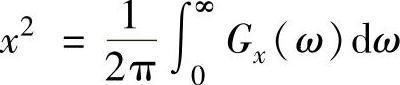。若考虑到车轮动载的均值近似为0，则有

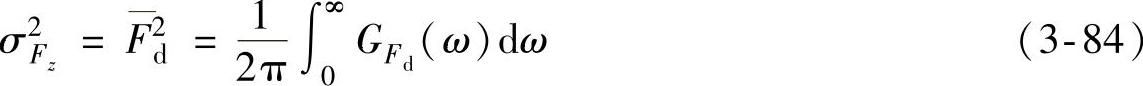
如果按不平度的谱密度计算车轮动载的方差，则为

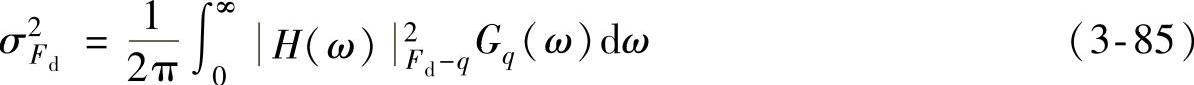
式中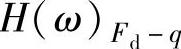，为频率响应函数。

在极端情况下，F_zs=-F_d，此时F_z=0，车轮不能传递水平力。如果这种情况出现在所有车轮上，车辆就丧失了驾驶的可能性，即使是一个车轮或某一车轴的两个车轮的附着力恶化，也会对汽车的行驶性能带来不利影响。因此，为了获得较高的安全性能，车轮法向力变化幅度应较小，这一点也表征为车轮法向力具有较小的标准差。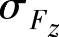

考虑到不同车辆的F_zs差异较大，车轮法向力的变化系数k_Fz应尽可能小，其定义为

如果要求各种载荷情况下行驶安全性大致相同，须有

最大车轮法向力F_zmax的大小不仅对道路应力有重要影响，而且对车轮和轮毂轴承的应力和使用寿命也有重要影响。定义车轮法向力冲击系数n_Fz为

当F_dmax取为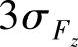时，则式（3-88）可表示为

车轮法向力冲击系数的值，比按式（3-89）所计算值大的概率仅为0.15%。

2.弹簧挠度

（1）座椅弹簧挠度 座椅弹簧总的挠度Δz由静挠度Δz_s和动挠度Δz_d所组成，如图3-17所示，即

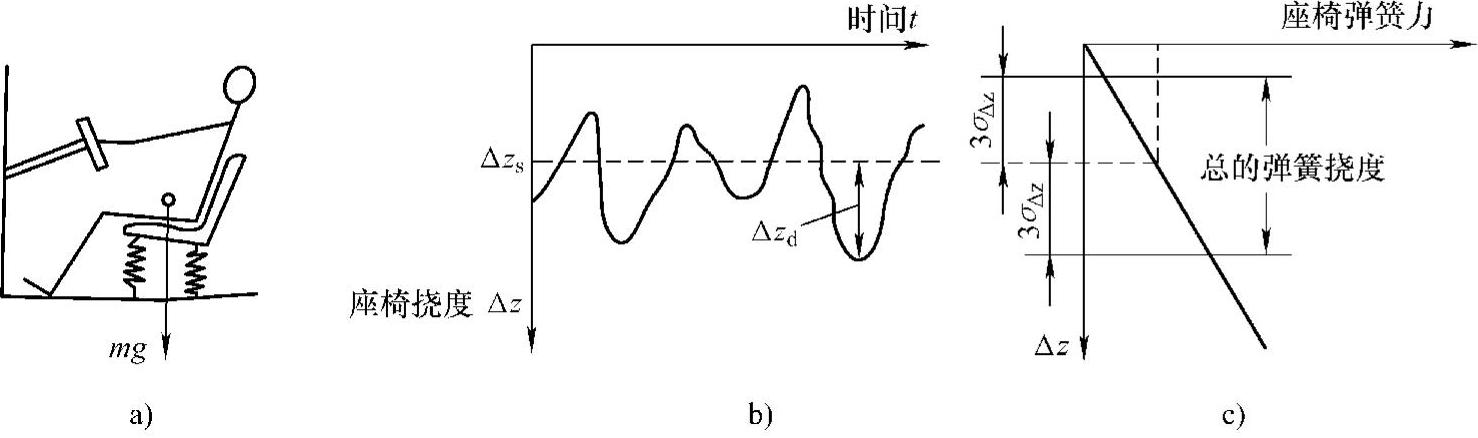
图3-17 座椅弹簧的挠度

a）座椅承受人体载荷 b）座椅弹簧的静挠度Δz_s和动挠度Δz_d c）结构设计时预留的动态弹簧挠度6σ_Δz

Δ_z（t）=Δz_s+Δz_d （3-90）当弹簧刚度为k、座椅上的静载质量为m时

考虑到无阻尼固有圆频率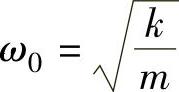，则式（3-91）化为

(www.xing528.com)

取g=980cm/s²，则当ω₀/2π=1Hz时，Δz_s=25cm；当ω₀/2π=0.5Hz时，Δz_s=100cm；当ω₀/2π=3Hz时，Δz_s=2.8cm。

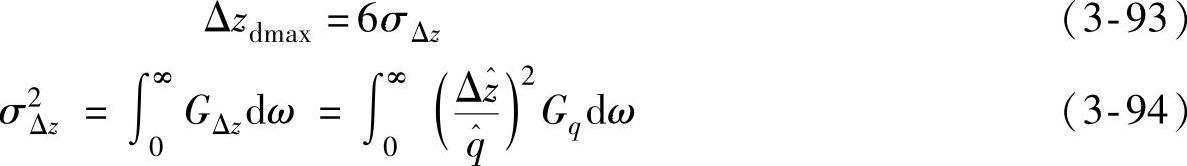
式中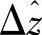，为座椅弹簧总挠度Δz的傅里叶变换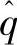；为路面激励q的傅里叶变换。

Δz_d不能过大，否则手和脚会出现误操作。

（2）悬架弹簧挠度 悬架弹簧的挠度如图3-18所示。

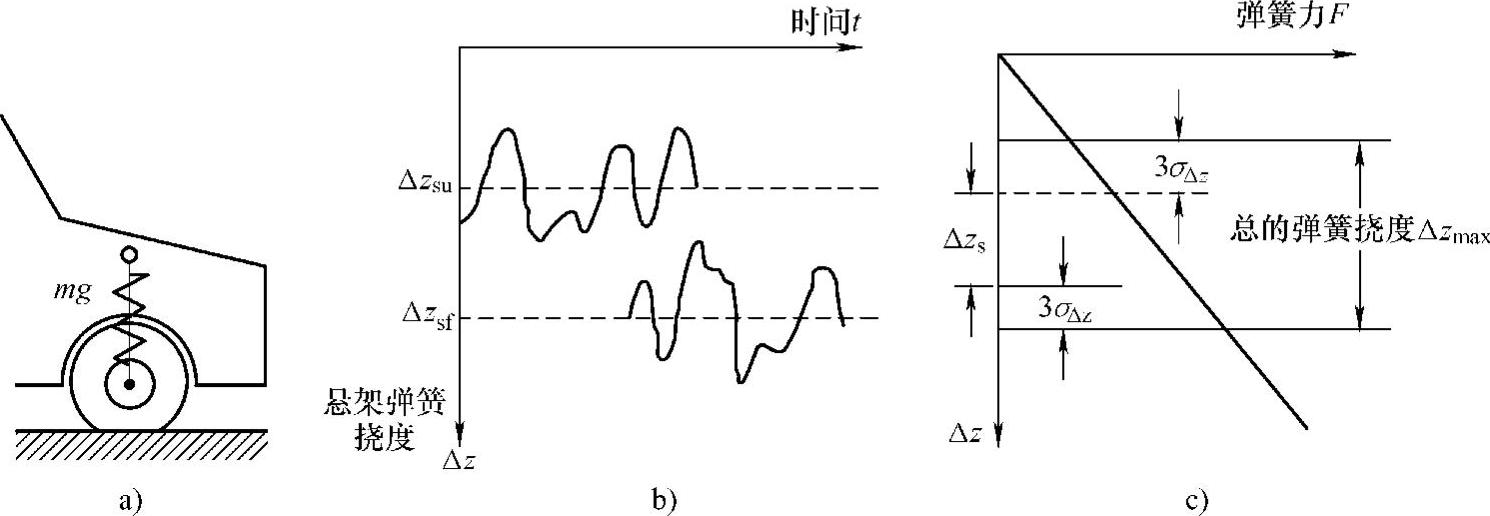
图3-18 悬架弹簧的挠度

a）车轮和车身之间弹簧所受静载荷 b）空载与满载车辆围绕静平衡位置的弹簧位移 c）用空载与满载车辆间动态弹簧压缩量差值和标准差来表示的弹簧挠度

因此，悬架弹簧的总挠度可表示为

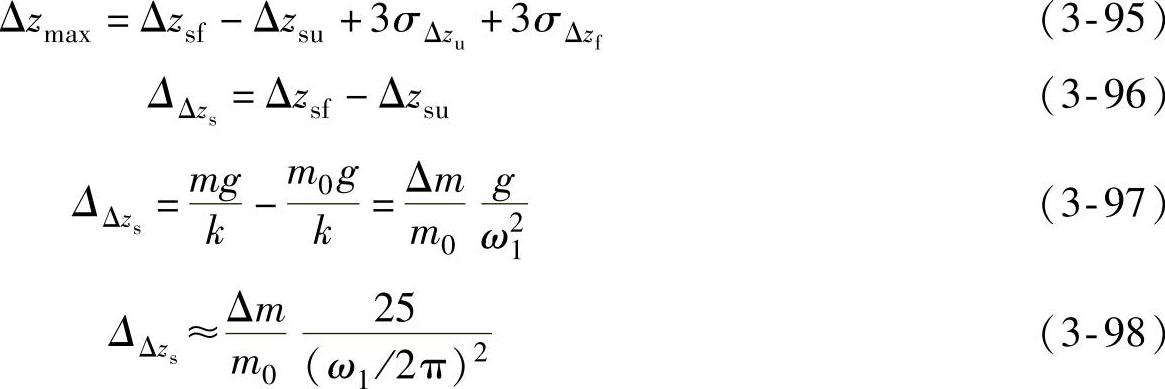
3.舒适性评价

舒适性是人的主观感受，对振动作用的评价不是只根据其强度，如不是单独根据加速度振幅的大小，而是对于同样强度但不同频率、部位和方向的振动有不同的感受。

（1）用以评价的振动强度、评价函数 为寻求评价的途径，让被试人员坐在振动椅上。振动座椅只能以单正弦波振动，但其频率和振幅可以用KZ表示“用以评价的振动强度”。它分成若干个等级，按主观感受“没有感觉”、“刚有感觉”、“有感觉”、“感觉强烈”、“感觉很强烈”进行划分，如图3-19所示。“KZ”中的“K”表示舒适，“Z”表示方向。

为了便于计算，引入评价函数为

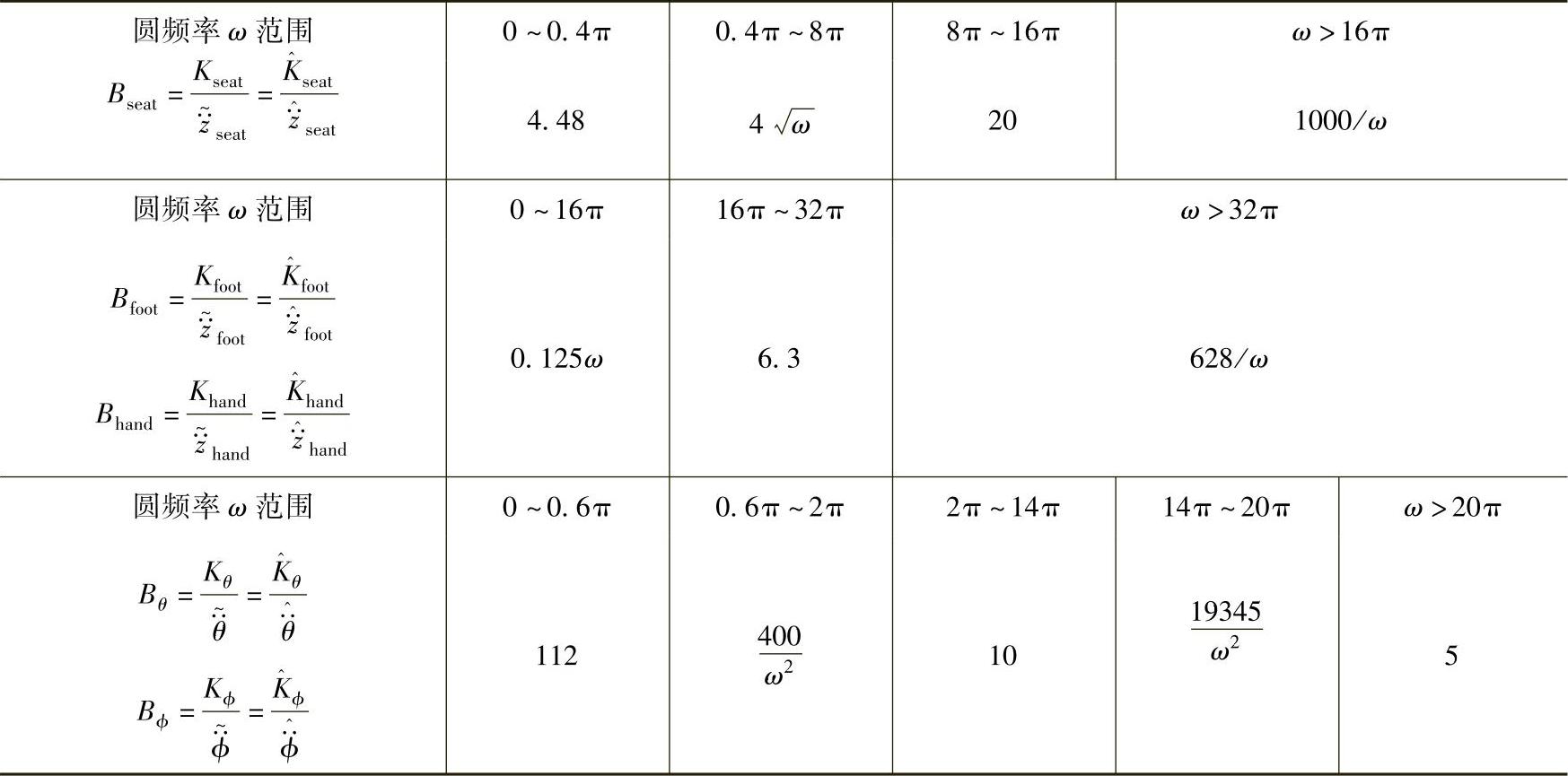
B_seat的曲线如图3-20所示。

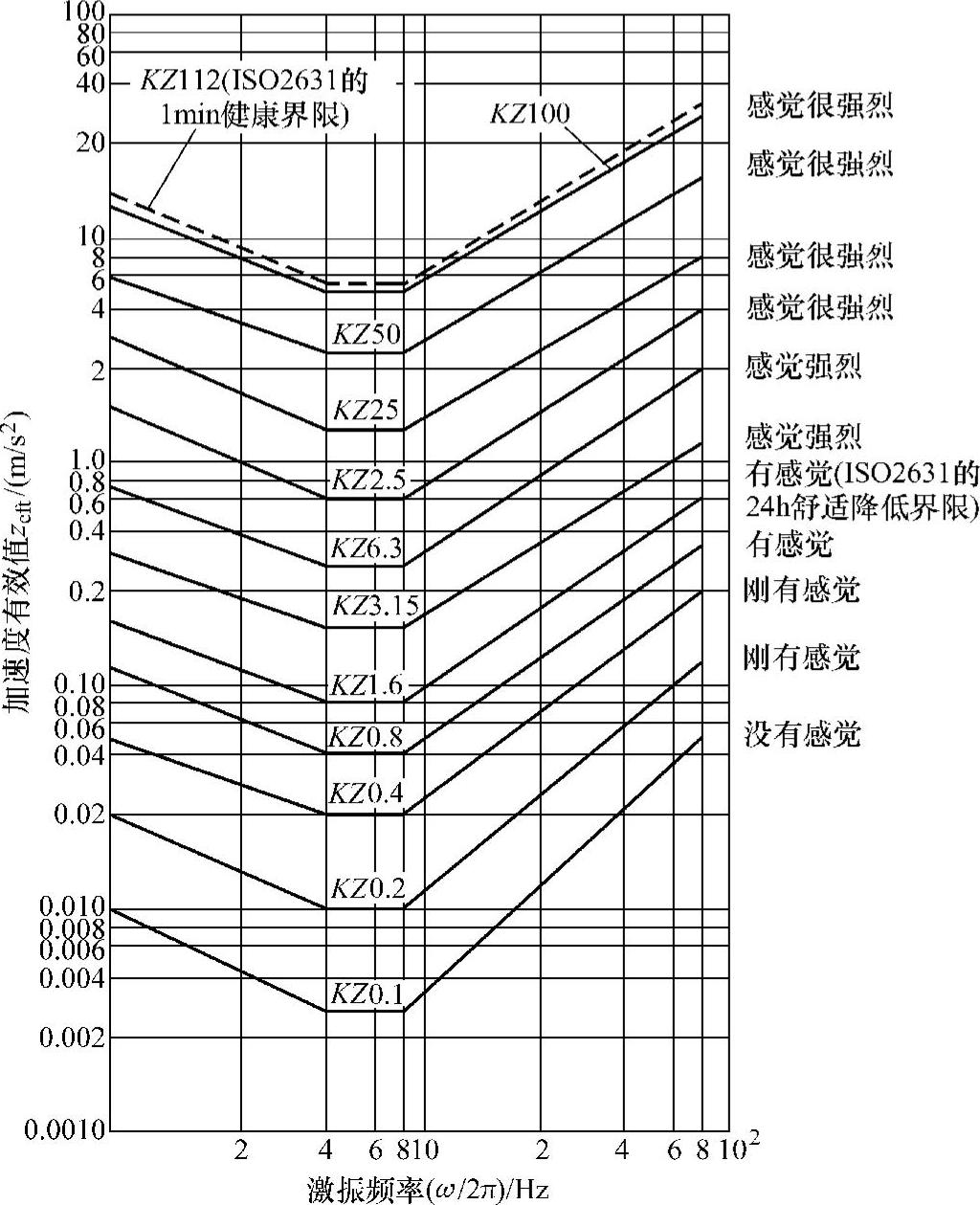
图3-19 KZ等值曲线与立姿、坐姿人体Z方向振动加速度和频率之间的关系

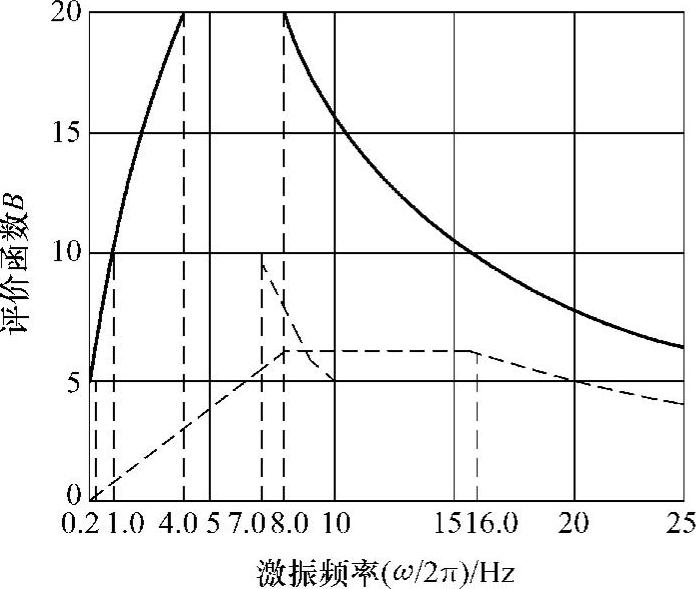
图3-20 车内人体所受振动的评价函数

计算公式见表3-5，表中还给出一些其他评价指标，如f=1Hz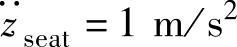，，K_seat=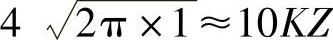，对应的主观感受为“感觉非常强烈”。

表3-5 评价函数的计算公式

人体最敏感的频率范围是：

1）对座椅上的人体承受垂直振动频率为4～12.5Hz。

2）侧倾运动振动频率应低于7Hz，特别是频率低于1Hz。

3）对双手和双脚的振动频率为8～16Hz。

（2）振动强度K的计算 如果振动中存在几个频率成分，则

当振动存在于一个频率范围内时，可利用傅里叶变换和谱密度等概念来求振动强度K。

即

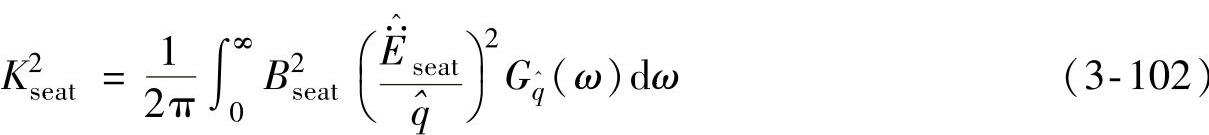
这里B_seat的定义与式（3-99）实质相同，但采用略有不同的形式，为

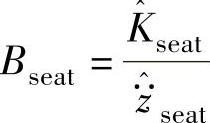
总的振动强度K_t为

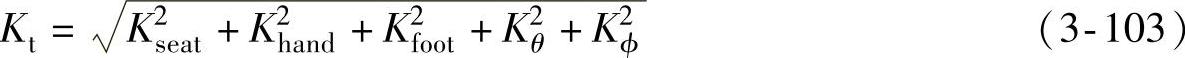
（3）作用时间 舒适程度可由舒适度降低界限、疲劳降低工作效率界限以及健康界限这三个界限来评价。这三个界限都是由振动强度K值和作用时间T共同决定的，如图3-21所示。

由如图3-21可知，在1～10min内，作用负荷是一样的。时间较长时，服从如下的分配规律

KT²=常数 （3-104）

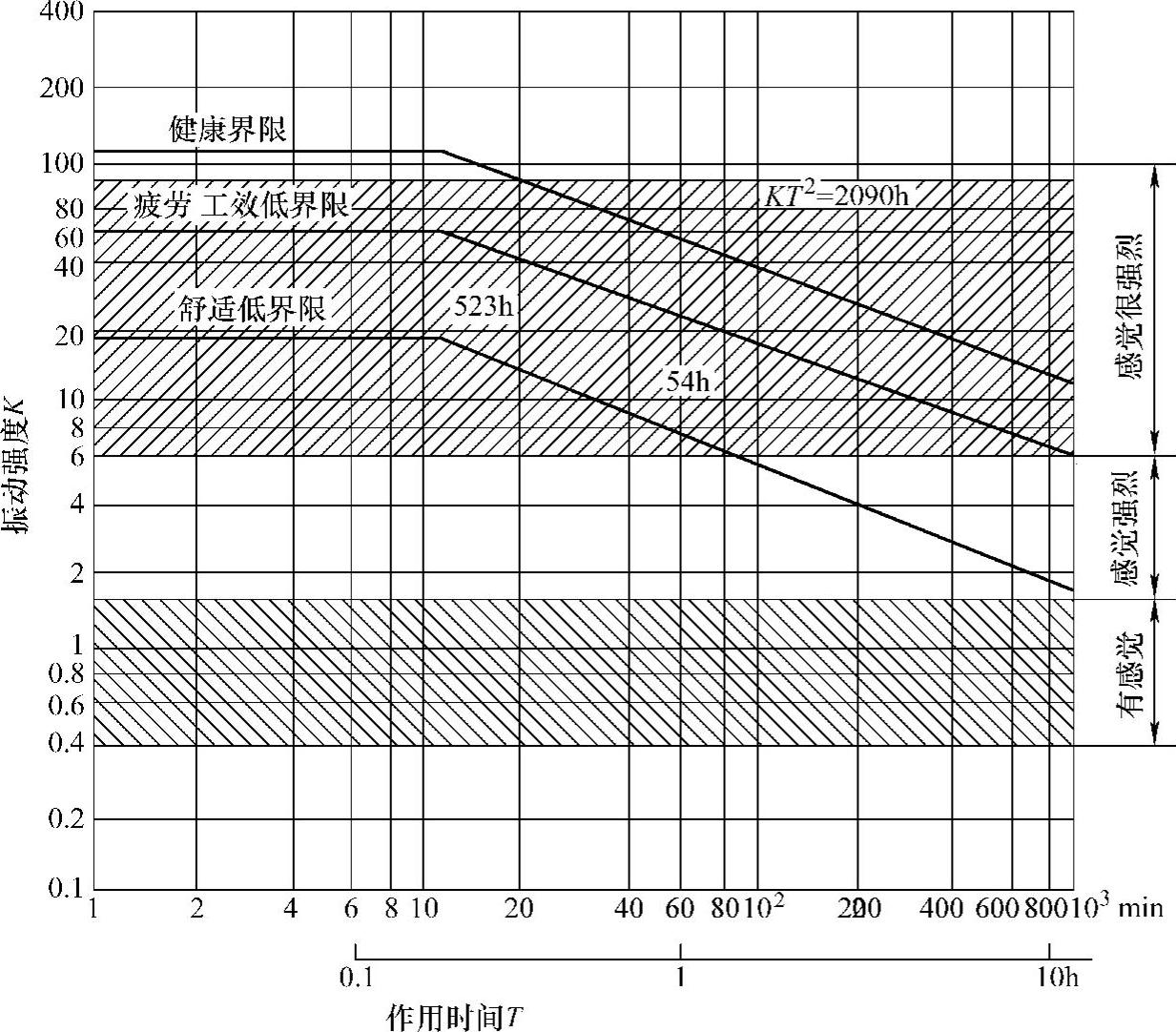
图3-21 按三个界限画出的振动强度与作用时间的关系