双质量系统参数对车辆平顺性的影响分析

为了分析双质量系统车身部分固有频率f₀、悬架阻尼比ξ、刚度比r_k和质量比r_m这四个参数对振动系统响应车身振动加速度、悬架动挠度δ_d和车辆相对动载F_d的影响，采用上述数值积分的方法，在B级路面、车速v=20m/s的情况下，对车身振动加速度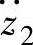、悬架动挠度δ_d和车辆相对动载w_d对路面激励速度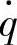的幅频特性和均方根值分别进行了计算。分析系统时的参数取值见表3-3。

表3-3 分析系统时的参数取值

1.车身固有频率f₀的影响分析

图3-9a、b、c所示为车身部分固有频率f₀分别为0.5Hz、1.0Hz、2.0Hz三种不同值（此时所对应的车轮部分的固有频率f_t=10f₀，相应分别为5Hz、10Hz和20Hz）、车轮阻尼比ξ_t=0.25为常数且其他参数保持不变时，车身振动加速度、悬架动挠度δ_d和车辆相对动载w_d对路面激励速度的幅频特性曲线。振动响应量的均方根值随固有频率f₀变化的曲线如图3-9d所示。

由图3-9可知，随着固有频率f₀的增加，车身振动加速度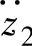和车辆相对动载w_d对路面激励速度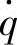的幅频特性，沿着斜率为+1的方向向右上方平移，而悬架动挠度δ_d路面激励速度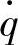的幅频特性沿着斜率为-1的方向向右下方平移。三个振动响应量的均方根值随着固有频率f₀的变化曲线如图3-9d所示。这表明，三个振动响应量对系统固有频率的变化是很敏感的。

图3-9 固有频率f₀对响应量的影响

2.车身阻尼比ξ的影响分析

图3-10a、b、c所示为车身部分阻尼比ξ分别为0.125、0.25、0.5三种不同值，其他参数f₀=1.0Hz、质量比r_m=10、刚度比r_k=9.0保持不变时，车身振动加速度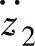、悬架动挠度δ_d、车辆相对动载w_d对路面激励速度的幅频特性曲线。此时，车轮部分的固有频率f_t=10Hz，ξ_t=ξ。振动响应量的均方根值随阻尼比的变化曲线，如图3-10d所示。

由图3-10可知，随着阻尼比ξ的增大，在低频共振区范围内的幅频特性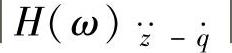、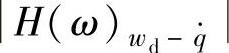的峰值均下降；而在低频和高频两个峰值之间，幅频特性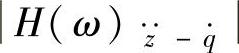、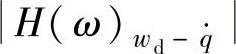的幅值都增大；在高频共振区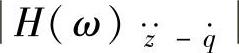，的幅值变化很小，而的幅值有明显的下降。当阻尼比ξ增大时，动挠度δ_d的幅频特性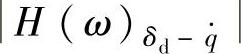在高频和低频两个共振区均显著下降，而在两个共振峰值之间变化比较小。

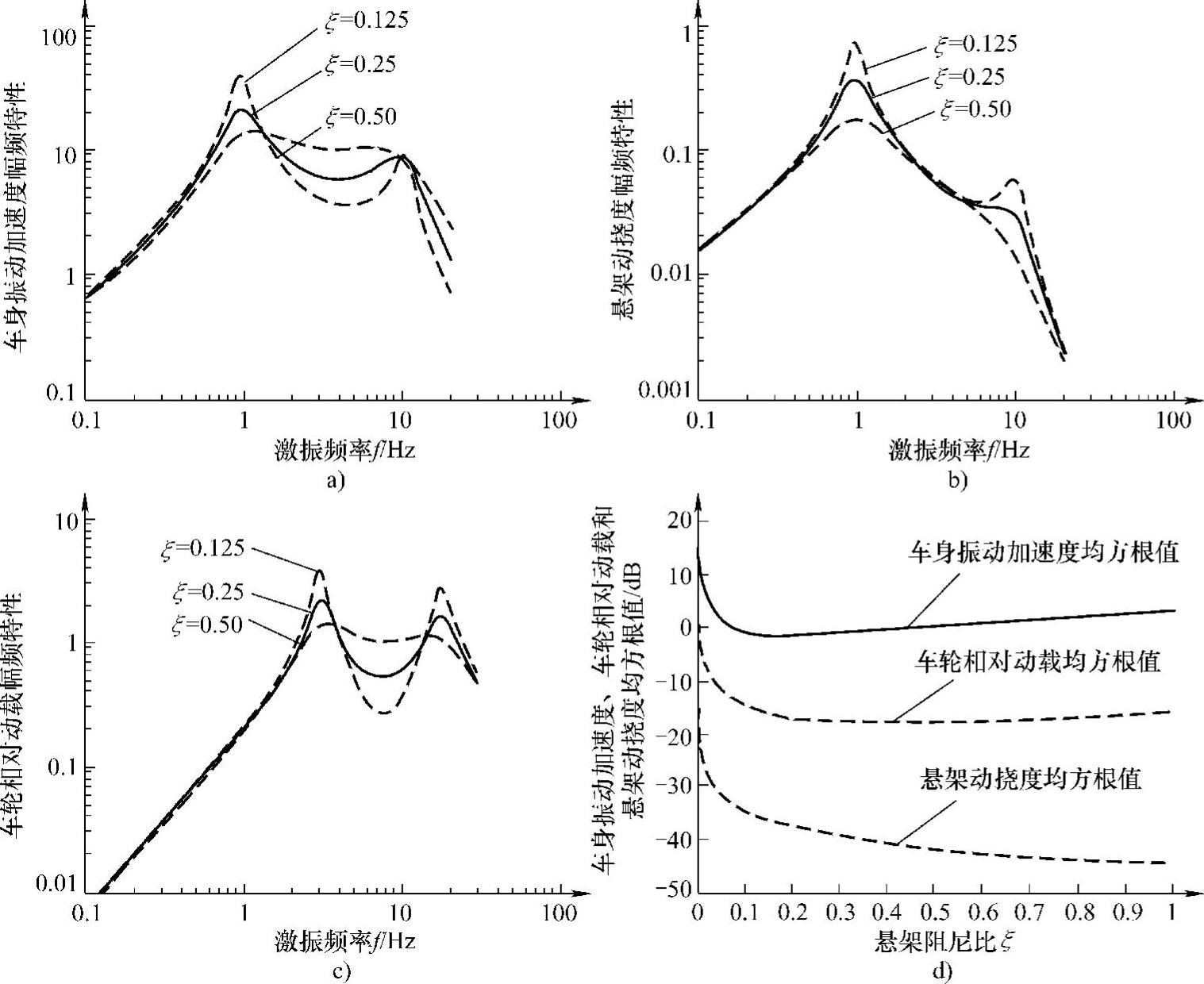
图3-10 车身阻尼比ξ对响应量的影响(www.xing528.com)

3.车身与车轮质量比r_m的影响分析

图3-11a、b、c所示为车身与车轮质量比r_m分别为5.0、10、20三种不同值，其他参数固有频率f₀、阻尼比ξ、刚度比r_k均保持不变时，车身振动加速度、悬架动挠度δ_d、车辆相对动载w_d对路面激励速度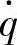的幅频特性曲线。

由图3-11a、b、c可知，当车身质量m₂一定时，质量比r_m改变相当于车轮部分质量m₁改变，则影响车轮部分的固有频率f_t和阻尼比ξ_t。r_m增大，相当于减小m₁，由车轮部分固有频率f_t和阻尼比ξ_t的计算公式可知，此时，f_t和ξ_t均提高，从而使三个响应量的幅频特性的高频共振峰值向高频方向移动，而峰值降低。由图3-11d中质量比r_m对车身振动加速度、悬架动挠度δ_d、车辆相对动载w_d三个响应量均方根值的关系曲线可以看出，质量比r_m增大，车身振动加速度均方根值和车轮动挠度均方根值σ_δd略有减小，主要是车轮相对动载的均方根值σ_wd变化较大。

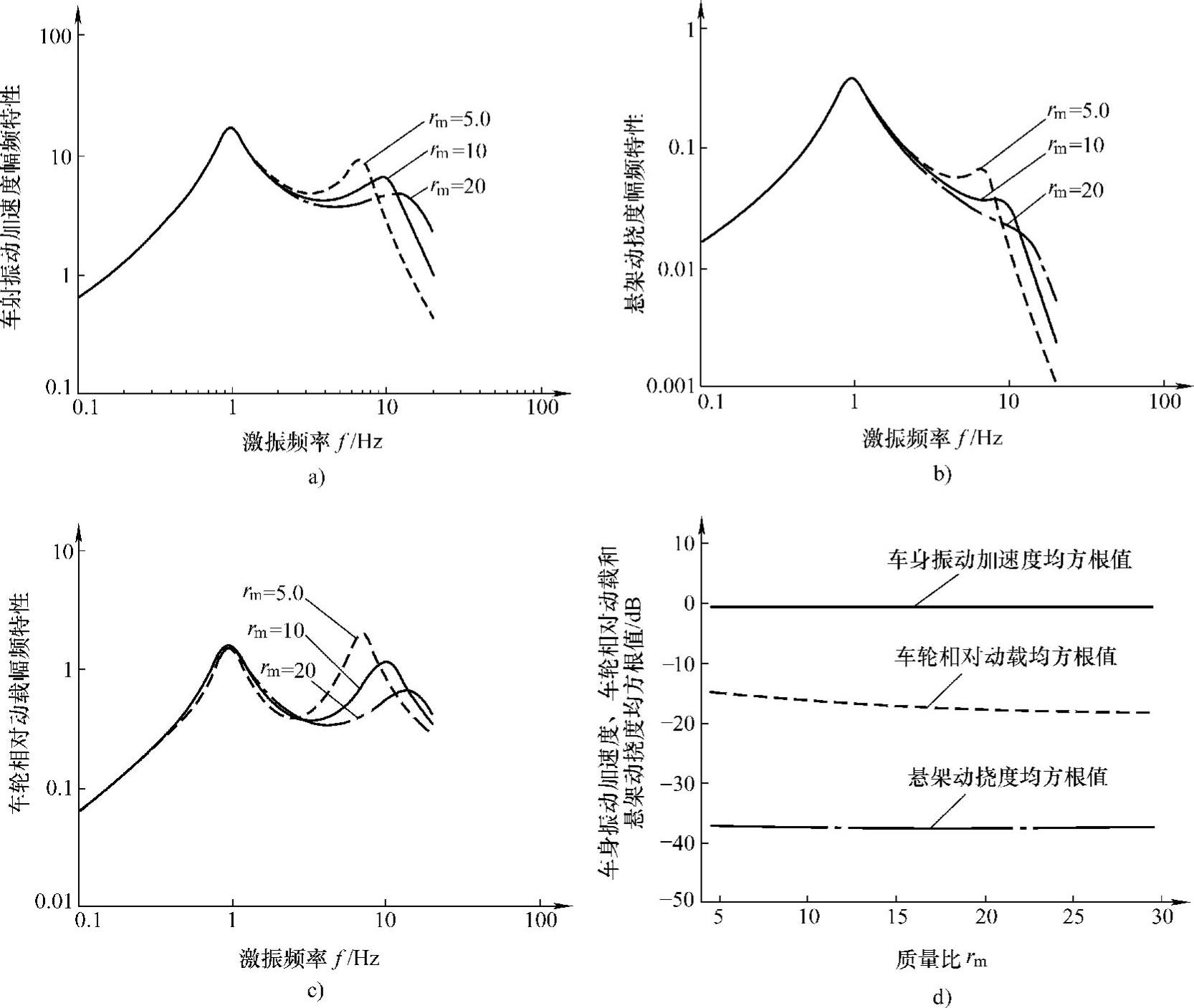
图3-11 车身与车轮质量比r_m对响应量的影响

4.悬架与轮胎刚度比r_k的影响分析

图3-12a、b、c所示为悬架与车轮刚度比r_k分别为4.5、9.0、18三种不同值，其他参数固有频率f₀、阻尼比ξ、刚度比r_k均保持不变时，车身振动加速度、悬架动挠度δ_d、车轮相对动载w_d对路面激励速度的幅频特性曲线。此时，悬架与车轮刚度比r_k增大，相当于悬架刚度k不变而轮胎刚度增大，从而使车轮部分系统参数变化，即车轮部分固有频率f_t提高，而阻尼比ξ_t下降，从而引起系统三个振动响应量的幅频特性高频共振峰值向右移动，且峰值提高。

其中，车轮相对动载w_d对路面激励速度的幅频特性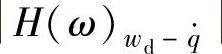变化最大，车身振动加速度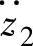对路面激励速度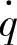的幅频特性次之，而悬架动挠度δ_d的幅频特性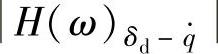的变化最小。

由图3-12d可知，悬架与车轮刚度比r_k对车轮相对动载w_d影响比较大，当刚度比r_k减小时，车轮相对动载降低，这表明，采用软的轮胎可改善平顺性，尤其是可以改善车轮的附着性能，提高车辆行驶安全性。

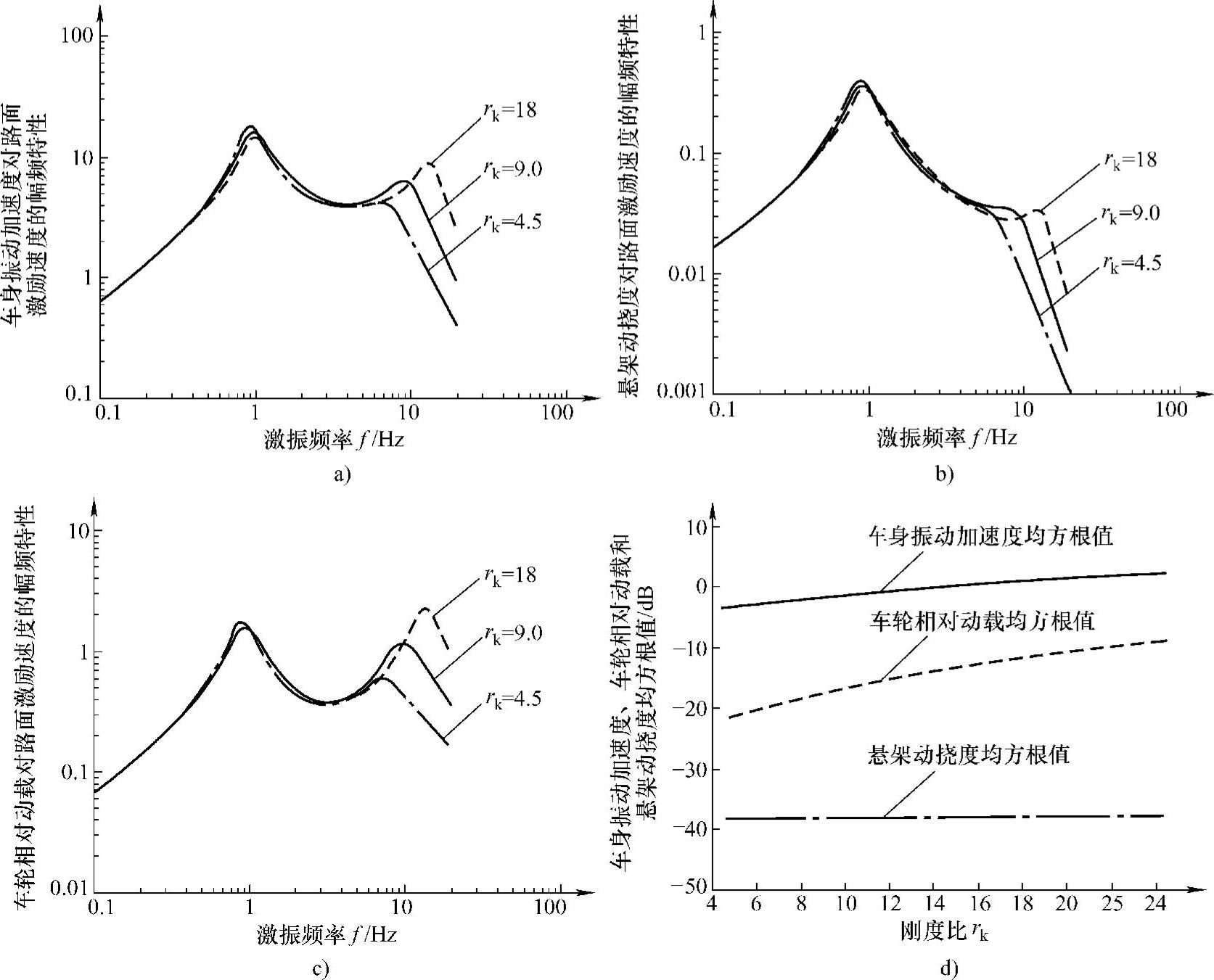
图3-12 悬架与轮胎刚度比r_k对响应量的影响