汽车减振器设计及特性仿真：提升车辆平顺性

1.双质量系统振动响应量的幅频特性

（1）车身振动加速度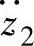对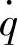的幅频特性 车身振动加速度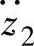对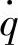的幅频特性为

车身m₂的振动响应z₂对路面激励位移q的幅频特性为

式中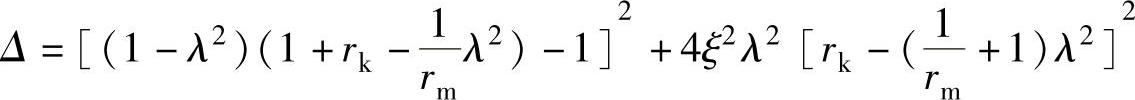，；λ为频率比，λ=ω/p₀；p₀为悬架固有圆频率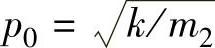，；r_k为刚度比，r_k=k_t/k；r_m为质量比，r_m=m₂/m₁。

将式（3-53）代入式（3-52），可得车身振动加速度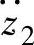对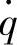的幅频特性应为

（2）相对动载F_d/G对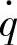的幅频特性

1）车轮动载为：F_d=k_t（z₁-q）。

2）车轮静载为：G=（m₂+m₁）g=m₁（r_m+1）g。

3）相对动载为：。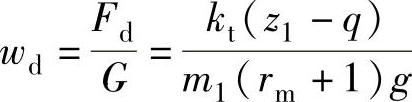

因此，相对动载w_d对路面激励位移q的频率响应函数为

车轮响应z₁对路面激励位移q的频率响应函数为

式中，A₁=jωc+k=k（1+2jξλ）；A₂=k-ω²m₂+jωc=k（1-λ²+2jξλ）；A₃=k+k_t-ω²m₁+jωc；N=A₃A₂-A²₁。

因此，车轮响应z₁对路面激励位移q的幅频特性为

将式（3-56）代入式（3-55），可得相对动载w_d对路面激励位移q的频率响应函数为

根据H（ω）_wd-q，可得到相对动载w_d对路面激励速度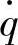的频率响应函数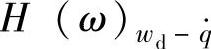，即

即

所以，车轮相对动载w_d对路面激励速度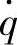的幅频特性为(www.xing528.com)

（3）悬架动挠度δ_d对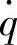的幅频特性 悬架动挠度δ_d对路面激励位移q的频率响应函数为

即

将式（3-56）和式（3-53）代入式（3-62），可得悬架动挠度δ_d对路面激励位移q的频率响应函数为

即

因此，悬架动挠度δ_d对路面激励速度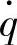的频率响应函数为

所以，悬架动挠度δ_d对路面激励速度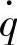的幅频特性为

2.双质量系统振动响应量的功率谱与均方根值

同理，根据单质量系统振动响应量的功率谱和均方根值的求解方法，可求得双质量系统振动响应量的功率谱与均方根值。具体计算过程为，按式（3-54）、式（3-61）、式（3-64）和悬架系统具体参数，求出振动响应量车身振动加速度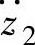、车轮动载荷w_d和悬架动挠度δ_d对路面激励速度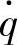的幅频特性，然后将由路面不平度系数G_q（n₀）和车速v所求得的路面激励速度的功率谱密度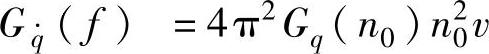，代入式（3-28）便求得车身振动加速度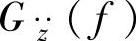、车轮相对动载荷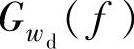和悬架动挠度的功率谱密度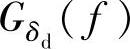，它们分别为

即

即

即

将式（3-65）～式（3-67）代入式（3-29），可求得振动响应量车身振动加速度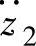、车轮相对动载荷w_d和悬架动挠度δ_d的均方值，分别为

式中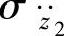，为车身振动加速度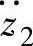的标准差，均值为零时等于均方根值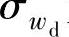；为车轮相对动载w_d的标准差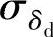；为悬架动挠度δ_d的标准差。

下面以振动加速度为例，计算汽车以速度v行驶时车身振动加速度的均方值。

将路面功率谱密度式（3-65）代入式（3-68），可得车身振动加速度的均方值为

由上式可以看出，当由系统参数所确定的车身振动加速度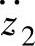对路面激励速度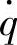的幅频特性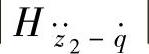一定时，车身m₂垂直振动响应加速度的均方值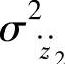与路面不平度系数G_q（n₀）以及车速v成正比。因此，不同路面的不平度系数和车速下的均方值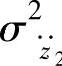，可以按G_q（n₀）和v数值变化的比例推算得出。