1.单质量系统振动响应量的幅频特性
(1)车身振动加速度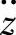 对
对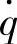 的幅频特性
的幅频特性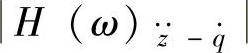 由定义可知,单质量车身振动加速度
由定义可知,单质量车身振动加速度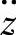 对
对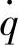 的幅频特性
的幅频特性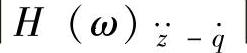 为
为
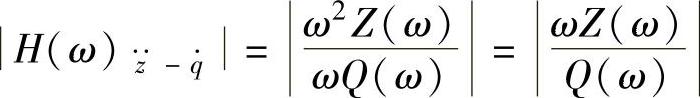
式中,Z(ω)为单质量车身振动响应位移z(t)的傅里叶变换;Q(ω)为路面激励位移q(t)的傅里叶变换。
由于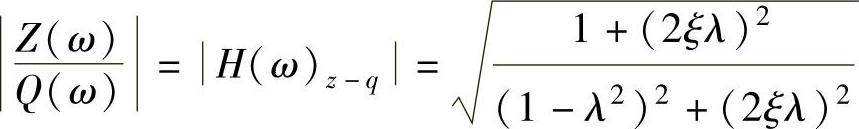 ,所以单质量车身振动加速度
,所以单质量车身振动加速度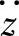 对q·的幅频特性
对q·的幅频特性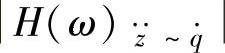 可化为
可化为
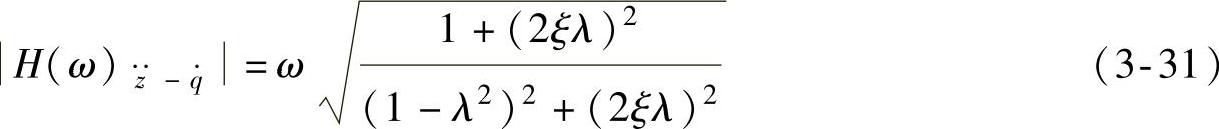
图3-5所示为两种不同固有频率ωn和阻尼比ξ情况下的车身振动加速度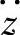 对
对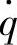 的幅频特性曲线。由曲线可以看出,随固有频率p0的提高,
的幅频特性曲线。由曲线可以看出,随固有频率p0的提高, 在共振段和高频段都成正比例提高。在共振时,激振频率ω等于系统圆频率p0,将ω=p0的代入式(3-31),可得
在共振段和高频段都成正比例提高。在共振时,激振频率ω等于系统圆频率p0,将ω=p0的代入式(3-31),可得
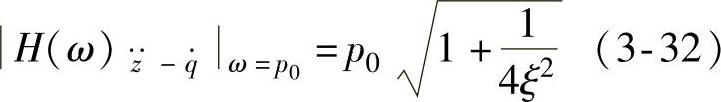
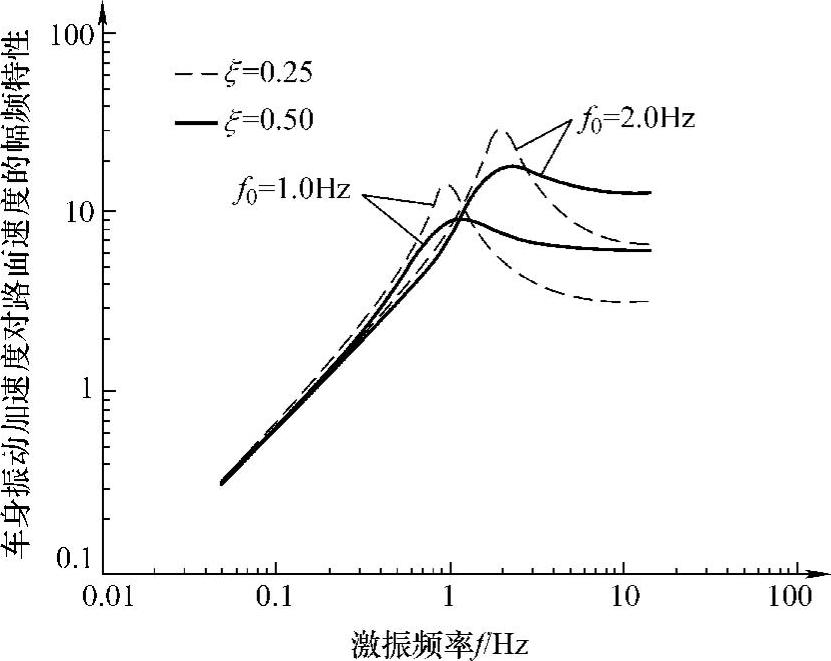
图3-5 单质量系统的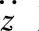 对
对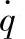 特性曲线
特性曲线
由此可知在共振点,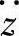 的均方根值谱与固有圆频率ωn成正比;在共振段,阻尼比ξ增大,
的均方根值谱与固有圆频率ωn成正比;在共振段,阻尼比ξ增大,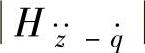 减小;在高频段,ξ增大,
减小;在高频段,ξ增大,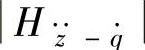 也增大,故ξ对共振段与高频段的效果相反。综合考虑,取单质量悬架系统的阻尼比ξ为0.2~0.4比较合适。
也增大,故ξ对共振段与高频段的效果相反。综合考虑,取单质量悬架系统的阻尼比ξ为0.2~0.4比较合适。
(2)车轮相对动载wd对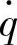 的幅频特性
的幅频特性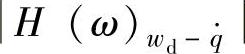 车轮与路面间的动载Fd与车轮作用于路面的静载G之比值Fd/G,称为相对动载wd。因此,单质量系统的车轮相对动载wd,可表示为
车轮与路面间的动载Fd与车轮作用于路面的静载G之比值Fd/G,称为相对动载wd。因此,单质量系统的车轮相对动载wd,可表示为

当相对动载wd>1时,车轮会跳离地面而完全失去附着,严重影响汽车的操纵稳定性和行驶安全性。
可见,单质量系统的车轮相对动载wd对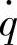 的幅频特性
的幅频特性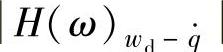 ,与
,与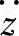 对
对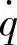 的幅频特性只相差系数1/g,其中g为重力加速度,即
的幅频特性只相差系数1/g,其中g为重力加速度,即
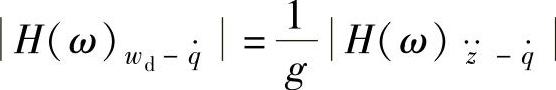
即
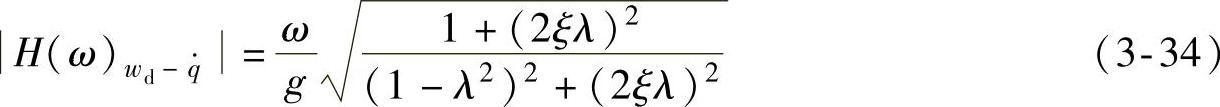
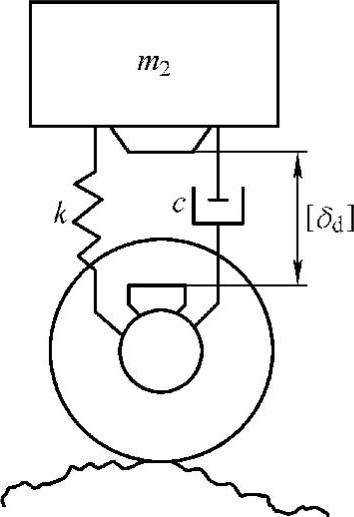
图3-6 限位行程示意图
因此,单质量系统固有频率ωn和阻尼比ξ对车轮相对动载的影响与上面讨论的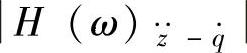 完全一样,在此不再赘述。
完全一样,在此不再赘述。
(3)悬架动挠度δd对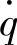 的幅频特性
的幅频特性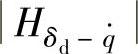 如图3-6所示,由车身平衡位置起,悬架允许的最大压缩行程就是其限位行程δd,动挠度δd必与限位行程[δd]应适当配合,否则会增加行驶中撞击限位的概率,使平顺性变坏。由图3-6可知,动挠度δd=z-q,所以动挠度δd对路面位移激励q的频率响应函数为
如图3-6所示,由车身平衡位置起,悬架允许的最大压缩行程就是其限位行程δd,动挠度δd必与限位行程[δd]应适当配合,否则会增加行驶中撞击限位的概率,使平顺性变坏。由图3-6可知,动挠度δd=z-q,所以动挠度δd对路面位移激励q的频率响应函数为
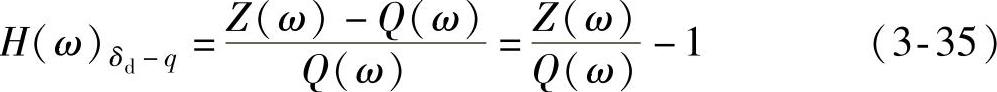
即

单轮响应的频响函数为

将式(3-37)代入式(3-36)得

因此,动挠度δd对路面位移激励q的幅频特性为
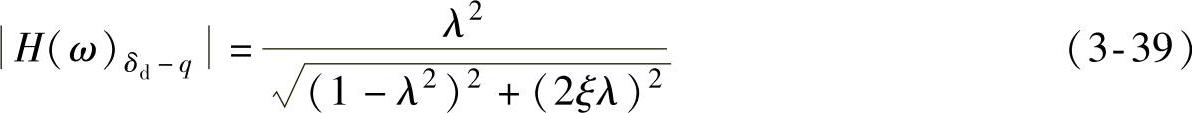
动挠度δd对路面位移激励q的幅频特性曲线如图3-7所示。
 (https://www.xing528.com)
(https://www.xing528.com)
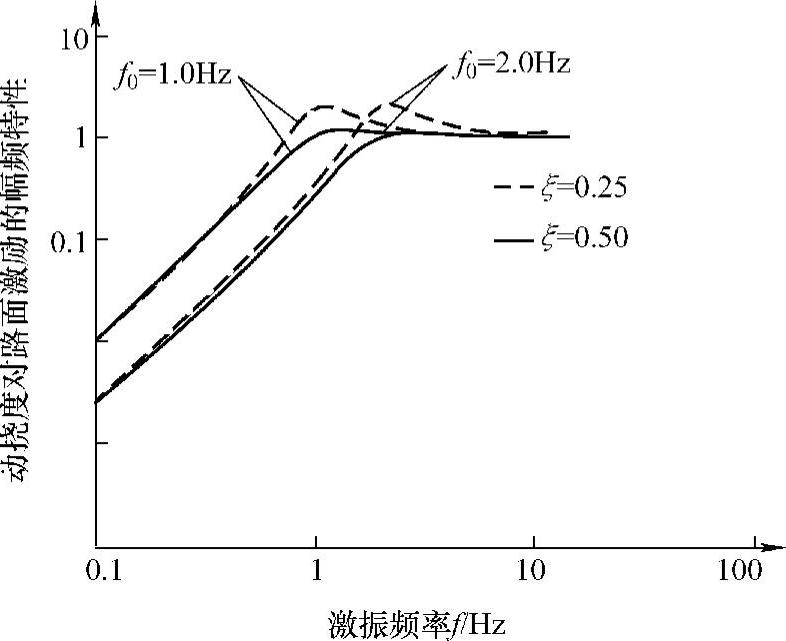
图3-7 δd对q的幅频特性曲线
由图3-7和式(3-39)可知:
1)在低频段,当λ<<1时,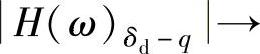 λ2对输入位移起衰减作用。
λ2对输入位移起衰减作用。
2)在高频段,当λ>>1时,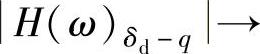 1,此时,车身位移z→0,即悬架变形与路面输入趋于相等。
1,此时,车身位移z→0,即悬架变形与路面输入趋于相等。
3)在共振段,当λ→1时,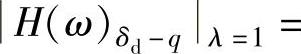
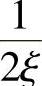 ,阻尼比对
,阻尼比对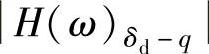 只在共振段起作用,而且当ξ=0.5时,
只在共振段起作用,而且当ξ=0.5时,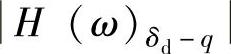 已不呈现峰值。
已不呈现峰值。
因为路面激励速度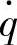 的傅里叶变换
的傅里叶变换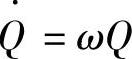 (ω),因此,动挠度δd对路面激励速度
(ω),因此,动挠度δd对路面激励速度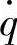 的幅频特性应为
的幅频特性应为
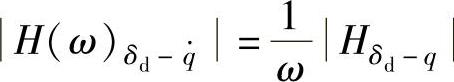
即

动挠度δd对路面激励速度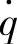 的幅频特性曲线如图3-8所示。图中给出了两种不同固有频率和阻尼比ξ情况下的
的幅频特性曲线如图3-8所示。图中给出了两种不同固有频率和阻尼比ξ情况下的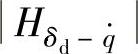 幅频特性曲线。
幅频特性曲线。
由图3-8曲线可以看出,随着固有频率p0的提高,幅频特性曲线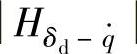 在共振段和低频段均与p0成正比例下降。
在共振段和低频段均与p0成正比例下降。
在共振时,激励频率ω等于悬架系统固有圆频率p0,即ω=p0,由式(3-39)和式(3-40)可得
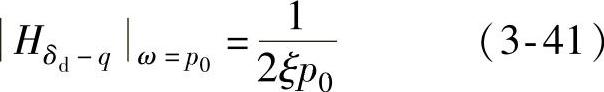
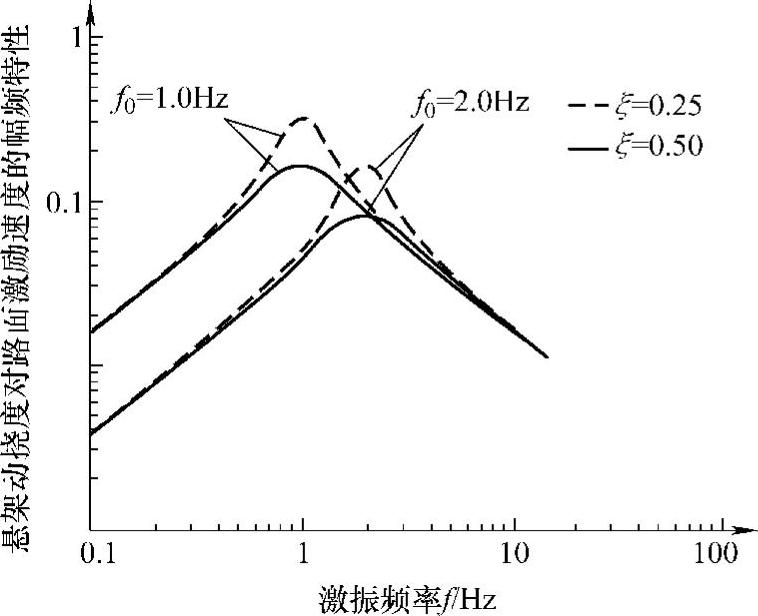
图3-8 δd对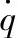 的幅频特性曲线
的幅频特性曲线
所以,共振点上δd的均方根值谱与悬架系统的固有频率p0和阻尼比ξ成反比,即共振点的动挠度随悬架弹簧刚度和减振器阻尼的增加而降低。
2.单质量系统振动响应量的功率谱与均方根值
当确定了路面不平度系数Gq(n0)和车速v之后,根据随机振动理论,可计算求得路面激励速度的功率谱密度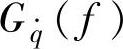
,即
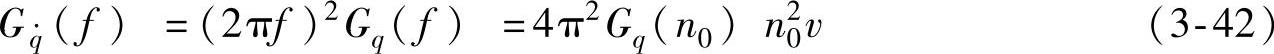
按式(3-31)、式(3-34)、式(3-40)和悬架系统具体参数,求出单质量系统的车身振动加速度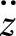 、车轮动载荷wd和悬架动挠度δd对路面激励速度
、车轮动载荷wd和悬架动挠度δd对路面激励速度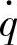 的幅频特性,然后将式(3-42)代入式(3-28),便求得单质量系统车身振动加速度
的幅频特性,然后将式(3-42)代入式(3-28),便求得单质量系统车身振动加速度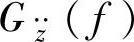 、车轮相对动载荷
、车轮相对动载荷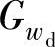 (f)和悬架动挠度的功率谱密度
(f)和悬架动挠度的功率谱密度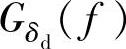 ,它们分别为
,它们分别为
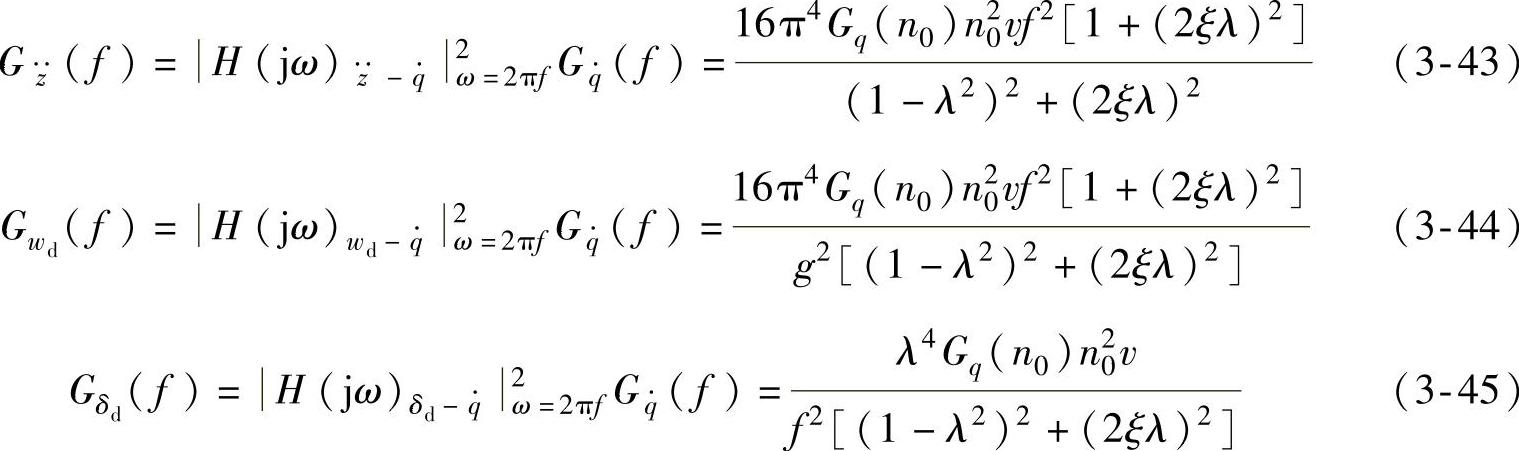
由于这三个振动响应量的均值为零,所以它们的方差都等于各自的均方值,而均方值可由其功率谱密度对频率积分式(3-29)求得。因此,将式(3-43)、式(3-44)和式(3-45)代入式(3-29),可求得单质量系统的振动响应量车身振动加速度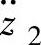 、车轮相对动载荷wd和悬架动挠度δd的均方值,分别为
、车轮相对动载荷wd和悬架动挠度δd的均方值,分别为
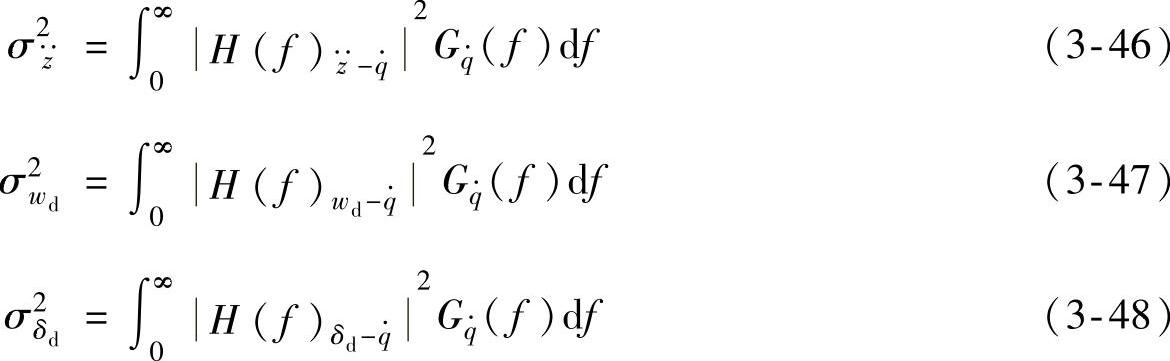
式中, 为单质量车身振动加速度
为单质量车身振动加速度 的标准差;σwd为车轮相对动载wd的标准差;σδd为悬架动挠度δd的标准差。
的标准差;σwd为车轮相对动载wd的标准差;σδd为悬架动挠度δd的标准差。
由于式(3-46)~式(3-48)中的幅频特性表达式相当复杂,一般难以用解析的方法直接进行积分,因此在工程上常采用数值积分的方法,即等间隔取N个离散频率值,频带宽度为Δf,因此,式(3-46)~式(3-48),可分别变为
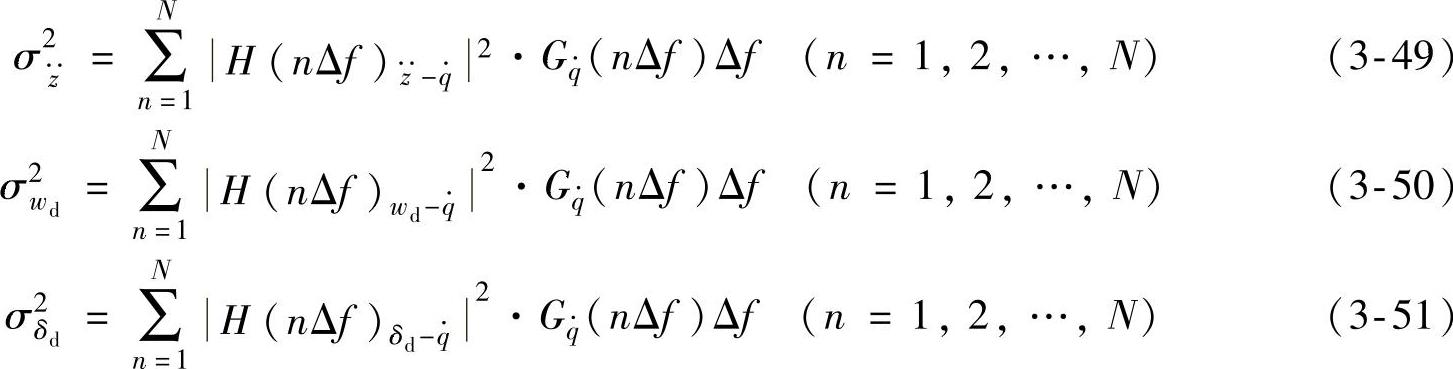
3.单质量系统参数对平顺性的影响及选择
由以上分析可知,降低固有频率f0,可明显降低车身振动加速度,即改善车辆行驶平顺性。但是,随着固有频率f0的降低,动挠度δd增大,因此,动挠度限位行程[δd]势必要随着固有频率f0的降低而增大,而车辆的动挠度限位行程[δd]是受到结构布置的限制的。对应给定车辆固有频率f0的情况下,降低阻尼比ξ,即减小悬架系统的阻尼系数cs,也可以提高车辆的舒适性,但是随着阻尼比ξ的降低,车辆动挠度将有所增加,同时,车轮相对动载将增加,从而使得车辆的行驶安全性降低。目前,车辆悬架系统固有频率f0、静挠度δs、限位行程[δd]和阻尼比ξ的实用选择范围见表3-2所示。
表3-2 悬架系统f0、δs、[δd]和ξ的选择范围
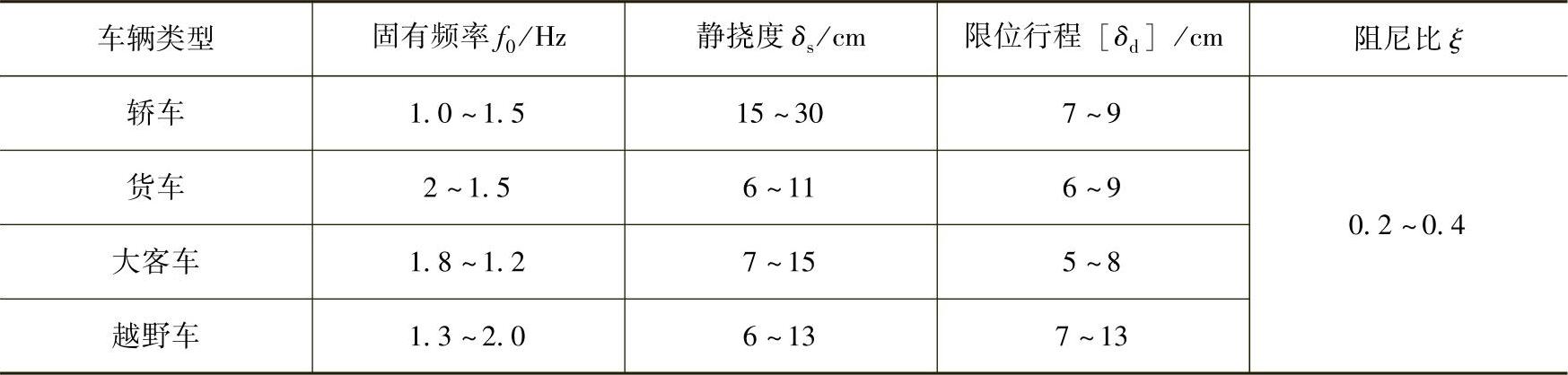
轿车舒适性要求比较高,而行驶路面也比货车和越野车的行驶路面相对较好,悬架动挠度δd引起的撞击限位的概率也很小,因此,轿车车身部分的固有频率可选择较低,以减小车身加速度,一般车身固有频率f0选择范围为1.0~1.5Hz。反之,货车和越野车由于行驶路面较差,为了减小悬架动挠度δd撞击限位的概率,车身固有频率f0选择偏高些,一般为1.5~2.0Hz。在固有频率f0比较低、行驶路面较差的情况下,动挠度会相当大,这时应选择偏大的阻尼比ξ,以降低撞击限位的概率。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




