汽车减振器设计仿真：功率谱密度与均方根值的影响

对于所讨论的汽车振动系统，路面只经一个车轮对系统输入并假设路面不平度函数为平稳随机过程，则线性系统平稳随机激励下的振动响应x包括车身振动加速度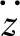、悬架动挠度δ_d和车轮动载荷F_d三个振动响应量，它们的功率谱密度G_x（f）与路面输入量的功率谱密度G_q（f）的关系可统一表示为

G_x（f）=H（f）x_-q^{2 G}q（f）（3-28）

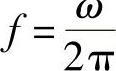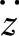式中，为频率（Hz）；H（f）x_-q即为幅频特性H（ω）x_-qω=2πf，下标x代表三个振动响应量、δd和F_d。由于车身振动加速度、悬架动挠度δ_d和车轮动载荷F_d三个振动响应量取正、负值的概率相同，所以其均值近似为零。因此，这些振动响应量的统计特征值——方差等于均方值。均方值可由其功率谱密度对频率积分求得，即

式中，σ_x为振动响应量的标准差，当均值为零时，它就等于均方根值。

进行平顺性分析时，通常根据路面不平度系数与车速共同确定的路面输入谱G_q（f）和由汽车悬架系统参数确定的频率响应函数H（f）x_-q，按式（3-28）和式（3-29）计算振动响应量的功率谱G_x（f）和均方根值σ_x。由此可以分析悬架系统参数对振动响应的影响，反过来也可根据汽车平顺性评价指标来优化悬架系统设计参数。(https://www.xing528.com)

路面输入除了利用式（3-29）中的位移谱G_q（f），还可以用速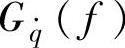度谱或加速度谱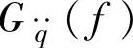与相应的幅频特性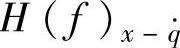或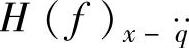的平方相乘，同样可以得到振动响应量的功率G_x（f）。

路面统计分析结果表明，路面速度功率谱在整个频率范围内为一常数，即“白噪声”，且常数只与路面不平度系数和车速有关，而与频率无关，即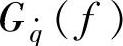恒为某个常数，这给平顺性计算分析带来极大方便。用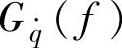作为输入谱代入式（3-28）并两边开方，得到输入与响应输出量均方根值谱之间的关系为

因为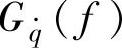为常数，即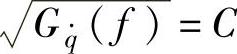，因此由式（3-30）可知，振动响应量的均方根值谱与响应量x对速度输入q·的幅频特性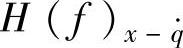的图形完全相同，只差某常数倍。所以，完全可以用响应量对速度输入的幅频特性来定性分析响应量的均方根值谱，为车轮行驶平顺性和安全性分析提供了方便。